洛谷 P3244 / loj 2115 [HNOI2015] 落忆枫音 题解【拓扑排序】【组合】【逆元】

组合计数的一道好题。什么非主流题目

题目背景

（背景冗长请到题目页面查看）

题目描述

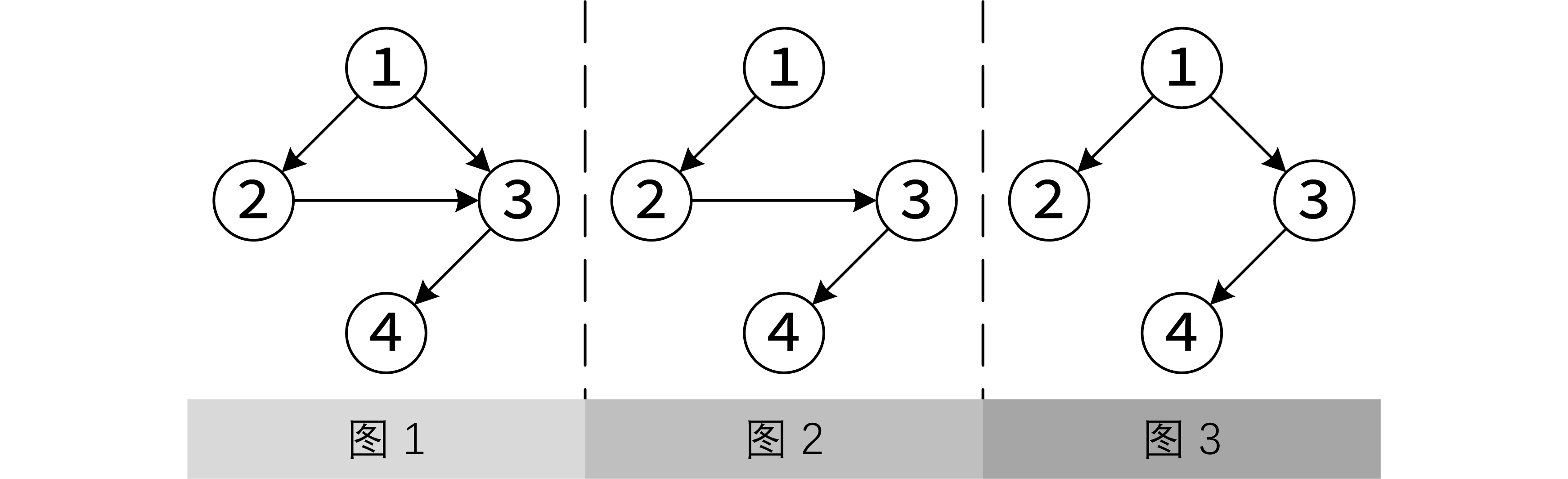
不妨假设枫叶上有 \(n​\) 个穴位，穴位的编号为 \(1\sim n​\)。有若干条有向的脉络连接着这些穴位。穴位和脉络组成一个有向无环图——称之为脉络图（例如图 1），穴位的编号使得穴位 \(1​\) 没有从其他穴位连向它的脉络，即穴位 1 只有连出去的脉络；由上面的故事可知，这个有向无环图存在一个树形子图，它是以穴位 \(1​\) 为根的包含全部 \(n​\) 个穴位的一棵树——称之为脉络树（例如图 2 和图 3 给出的树都是图 1 给出的脉络图的子图）；值得注意的是，脉络图中的脉络树方案可能有多种可能性，例如图 2 和图 3 就是图 1 给出的脉络图的两个脉络树方案。

脉络树的形式化定义为：以穴位 \(r\) 为根的脉络树由枫叶上全部 \(n\) 个穴位以及 \(n-1\) 条脉络组成，脉络树里没有环，亦不存在从一个穴位连向自身的脉络，且对于枫叶上的每个穴位 \(s\)，都存在一条唯一的包含于脉络树内的脉络路径，使得从穴位 \(r\) 出发沿着这条路径可以到达穴位 \(s\)。

现在向脉络图添加一条与已有脉络不同的脉络（注意：连接 \(2\) 个穴位但方向不同的脉络是不同的脉络，例如从穴位 \(3\) 到 \(4\) 的脉络与从 \(4\) 到 \(3\) 的脉络是不同的脉络，因此，图 1 中不能添加从 \(3\) 到 \(4\) 的脉络，但可添加从 \(4\) 到 \(3\) 的脉络），这条新脉络可以是从一个穴位连向自身的（例如，图 1 中可添加从 \(4\) 到 \(4\) 的脉络）。原脉络图添加这条新脉络后得到的新脉络图可能会出现脉络构成的环。

请你求出添加了这一条脉络之后的新脉络图的以穴位 \(1\) 为根的脉络树方案数。

由于方案可能有太多太多，请输出方案数对 \(1000000007\) 取模得到的结果。

输入格式

输入文件的第一行包含四个整数 \(n\)、\(m\)、\(x\) 和 \(y\)，依次代表枫叶上的穴位数、脉络数，以及要添加的脉络是从穴位 \(x\) 连向穴位 \(y\) 的。

接下来 \(m\) 行，每行两个整数，由空格隔开，代表一条脉络。第 \(i\) 行的两个整数为 \(u_i\) 和 \(v_i\)，代表第 \(i\) 条脉络是从穴位 \(u_i\) 连向穴位 \(v_i\) 的。

输出格式

输出一行，为添加了从穴位 \(x\) 连向穴位 \(y\) 的脉络后，枫叶上以穴位 \(1\) 为根的脉络树的方案数对 \(1000000007\) 取模得到的结果。

输入输出样例

输入样例：

4 4 4 3
1 2
1 3
2 4
3 2

输出样例：

3

数据范围与约定

对于所有测试数据，\(1\leq n\leq 100000, \ n-1 \leq m \leq \min \left(200000, \frac{n(n - 1)}{2}\right), \ 1 \leq x, y, u_i, v_i \leq n​\)。

题解：

首先需要找出一个不需要拓扑排序就能解决不加边时的脉络树数量的方法。

对于每个点 \(u(u\ge 2)\) ，假定它的入度为 \(d_i\) ，则它有 \(d_i\) 个父亲可供选择。我们只需要从上往下看，就可以发现每一层都是互相独立的，因此加边之前脉络树的数量为

\[\prod_{i=2}^nd_i
\]

此时考虑加边。正常情况下按上面的方式计数，边数为 \(n-1\) 的图的总数 \(sum\) 为

\[sum=\prod_{i=2}^n\left(d_i+[i=y]\right)
\]

但是实际上不是所有 \(sum\) 种方案都符合题意，由于每个点选择父亲是自由从入边选的，因此可能存在环，此时就不满足”脉络树“的定义了，而且图/树也没有明显分层。

我们考虑所有的 \(sum​\) 种方案，从中减掉包含环的那些方案。由于我们加入的边是 \(\left<x,y\right>​\)，所以一定是与路径 \(y\to x​\) 成环。因此我们只需要排除那些包含 \(y\to x\) 的路径的边数为 \(n-1​\) 的图就可以了。

注意由于加了新边之后的图只有一个环，因此 \(n-1​\) 条边的图也最多只有一个环。

话再说回来，包含 \(y\to x​\) 的路径的图我们可以认为这条路径上的所有点（包括 \(x,y​\)）都被钦定了一个父亲（其中 \(x​\) 的父亲认为是 \(y​\)，因为要成环）。假设用 \(S=\left\{a_i\right\}​\) 表示这条路径，那么包含 \(y\to x​\) 的图种类数就是 \(\prod_{i\notin S}d_i​\)。

而最终的答案就是 \(sum-\sum_{S:y\to x}\prod_{i\notin S}d_i​\)。

此时考虑如何求出所有的 \(y\to x\)。可以建立原图的反向边，跑拓扑排序。设定状态 \(f_k\) 表示 \(\sum_{S:k\to x}\prod_{i\notin S}d_i\)，每次从原图的边 \(\left<u,v\right>\) 转移时，即钦定了 \(v\) 的入边，所以状态转移方程为

\[f_u=\sum_{\left<u,v\right>\in E}\frac{f_v}{d_v}
\]

由于我们还要钦定 \(x\) 的入边是 \(y\)，因此最终的答案是

\[ans=sum-\frac{f_x}{d_x}
\]

时间复杂度为 \(O(n)\) 或 \(O(n\log n)\) （在线求逆元）

Code：

#include<cstdio>
#include<cstring>
#define p 1000000007
int Plus(int x,int y)
{return (x+y>=p)?(x+y-p):(x+y);}
int Mul(int x,int y)
{return 1ll*x*y%p;}
struct edge
{
    int n,nxt;
    edge(int n,int nxt)
    {
        this->n=n;
        this->nxt=nxt;
    }
    edge(){}
}e[200000];
int head[100100],ecnt=-1;
void add(int from,int to)
{
    e[++ecnt]=edge(to,head[from]);
    head[from]=ecnt;
}
int d[100100],in[100100];
//d表示真实入度 in表示拓扑排序中的入度
int q[100100],l=0,r=0;
int f[100100],inv[100100];
int main()
{
    memset(head,-1,sizeof(head));
    inv[1]=1;
    for(int i=2;i<=100000;++i)
        inv[i]=Mul(p-p/i,inv[p%i]);
    int n,m,x,y,u,v;
    scanf("%d%d%d%d",&n,&m,&x,&y);
    for(int i=1;i<=m;++i)
    {
        scanf("%d%d",&u,&v);
        add(v,u);
        ++in[u];
        ++d[v];
    }
    f[x]=1;
    int sum=1;
    for(int i=2;i<=n;++i)
    {
        if(!in[i])
            q[++r]=i;
        f[x]=Mul(f[x],d[i]);
        sum=Mul(sum,d[i]+(i==y));
    }
    if(y==1)
    {
        printf("%d\n",sum);
        return 0;
    }
    while(l<r)
    {
        int k=q[++l];
        for(int i=head[k];~i;i=e[i].nxt)
        {
            --in[e[i].n];
            f[e[i].n]=Plus(f[e[i].n],Mul(f[k],inv[d[k]]));
            if(!in[e[i].n])
                q[++r]=e[i].n;
        }
    }
    printf("%d\n",Plus(sum,p-Mul(f[y],inv[d[y]])));
    return 0;
}