bzoj 1005 组合数学 Purfer Sequence

这题需要了解一种数列： Purfer Sequence

我们知道，一棵树可以用括号序列来表示，但是，一棵顶点标号（1~n）的树，还可以用一个叫做 Purfer Sequence 的数列表示

一个含有 n 个节点的 Purfer Sequence 有 n-2 个数，Purfer Sequence 中的每个数是 1~n 中的一个数

一个定理：一个 Purfer Sequence 和一棵树一一对应

先看看怎么由一个树得到 Purfer Sequence

由一棵树得到它的 Purfer Sequence 总共需要 n-2 步，每一步都在当前的树中寻找具有最小标号的叶子节点（度为 1），将与其相连的点的标号设为 Purfer Sequence 的第 i 个元素，并将此叶子节点从树中删除，直到最后得到一个长度为 n-2 的 Purfer Sequence 和一个只有两个节点的树

看看下面的例子：

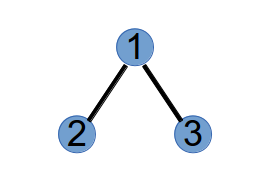
假设有一颗树有 5 个节点，四条边依次为：(1, 2), (1, 3), (2, 4), (2, 5)，如下图所示：

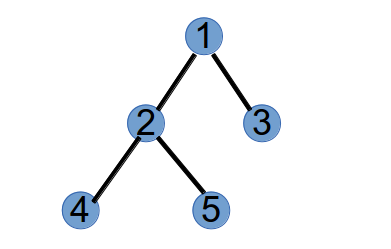
第 1 步，选取具有最小标号的叶子节点 3，将与它相连的点 1 作为第 1 个 Purfer Number，并从树中删掉节点 3：

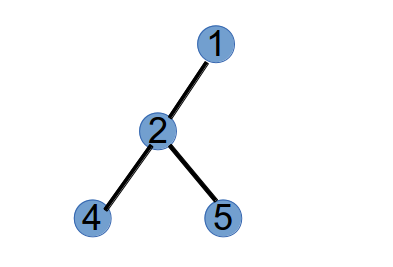
第 2 步，选取最小标号的叶子节点 1，将与其相连的点 2 作为第 2 个 Purfer Number，并从树中删掉点 1：

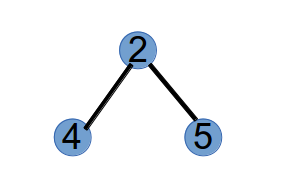
第 3 步，选取最小标号的叶子节点 4，将与其相连的点 2 作为第 3 个 Purfer Number，并从树中删掉点 4：

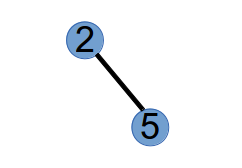
最后，我们得到的 Purfer Sequence 为：1 2 2

不难看出，上面的步骤得到的 Purfer Sequence 具有唯一性，也就是说，一个树，只能得到一个唯一的 Purfer Sequence

接下来看，怎么由一个 Purfer Sequence 得到一个树

由 Purfer Sequence 得到一棵树，先将所有编号为 1 到 n 的点的度赋初值为 1，然后加上它在 Purfer Sequence 中出现的次数，得到每个点的度

先执行 n-2 步，每一步，选取具有最小标号的度为 1 的点 u 与 Purfer Sequence 中的第 i 个数 v 表示的顶点相连，得到树中的一条边，并将 u 和 v 的度减一

最后再把剩下的两个度为 1 的点连边，加入到树中

我们可以根据上面的例子得到的 Purfer Sequence ：1 2 2 重新得到一棵树

Purfer Sequence 中共有 3 个数，可以知道，它表示的树中共有 5 个点，按照上面的方法计算他们的度为下表所示：

顶点	1	2	3	4	5
度	2	3	1	1	1

第 1 次执行，选取最小标号度为 1 的点 3 和 Purfer Sequence 中的第 1 个数 1 连边：

将 1 和 3 的度分别减一：

顶点	1	2	3	4	5
度	1	3	0	1	1

第 2 次执行，选取最小标号度为 1 的点 1 和 Purfer Sequence 中的第 2 个数 2 连边：

将 1 和 2 的度分别减一：

顶点	1	2	3	4	5
度	0	2	0	1	1

第 3 次执行，将最小标号度为 1 的点 4 和 Purfer Sequence 第 3 个数 2 连边：

将 2 和 4 的度分别减一：

顶点	1	2	3	4	5
度	0	1	0	0	1

最后，还剩下两个点 2 和 5 的度为 1，连边：

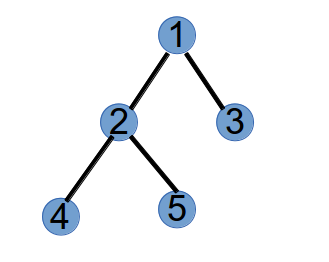
至此，一个 Purfer Sequence 得到的树画出来了，由上面的步骤可知，Purfer Sequence 和一个树唯一对应

综上，一个 Purfer Sequence 和一棵树一一对应

有了 Purfer Sequence 的知识，这题怎么搞定呢？

先不考虑无解的情况，从 Purfer Sequence 构造树的过程中可知，一个点的度数减一表示它在 Purfer Sequence 中出现了几次，那么：

假设度数有限制的点的数量为 cnt，他们的度数分别为：d[i]

另：

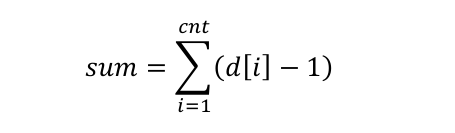
那么，在 Purfer Sequence 中的不同排列的总数为：

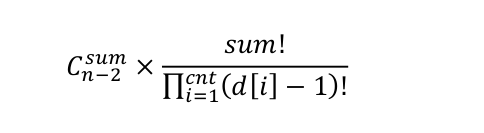
而剩下的 n-2-sum 个位置，可以随意的排列剩余的 n-cnt 个点，于是，总的方案数就应该是：

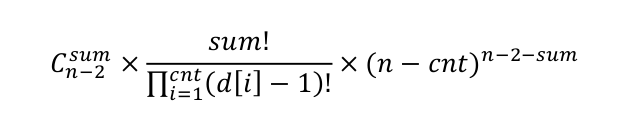
化简之后为：

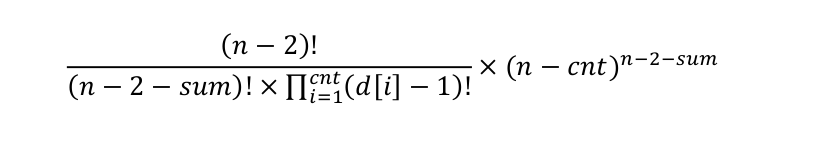
以上题解转自http://www.cnblogs.com/zhj5chengfeng/p/3278557.html

//By BLADEVIL
var
    n                        :longint;
    d                        :array[..] of int64;
    a, b, c                    :array[..] of int64;
 
procedure init;
var
    i                        :longint;
begin
    read(n);
    for i:= to n do read(d[i]);
end;
 
function mul(s1,s2:ansistring):ansistring;
var
    len1, len2                :int64;
    i, j                    :longint;
    s                        :ansistring;
 
begin
    fillchar(a,sizeof(a),);
    fillchar(b,sizeof(b),);
    fillchar(c,sizeof(c),);
    len1:=length(s1);
    len2:=length(s2);
    for i:= to len1 do a[(len1-i) div +]:=a[(len1-i) div +]*+ord(s1[i])-;
    for i:= to len2 do b[(len2-i) div +]:=b[(len2-i) div +]*+ord(s2[i])-;
 
    len1:=(len1+) div ;
    len2:=(len2+) div ;
    for i:= to len1 do
        for j:= to len2 do
        begin
            c[i+j-]:=c[i]+a[i]*b[j];
            c[i+j]:=c[i+j-] div ;
            c[i+j-]:=c[i+j-] mod ;
        end;
    mul:='';
    inc(len1);
    for i:=len1 downto  do
    begin
        str(c[i],s);
        if c[i]< then mul:=mul+'';
        if c[i]< then mul:=mul+'';
        if c[i]< then mul:=mul+'';
        if c[i]< then mul:=mul+'';
        if c[i]< then mul:=mul+'';
        if c[i]< then mul:=mul+'';
        if c[i]< then mul:=mul+'';
        mul:=mul+s;
    end;
    while (mul[]='') and (length(mul)>) do delete(mul,,);
end;
 
function divide(s:ansistring;x:int64):ansistring;
var
    len                        :int64;
    i                        :longint;
 
begin
    fillchar(a,sizeof(a),);
    fillchar(c,sizeof(c),);
    len:=length(s);
    for i:= to len do a[(len-i) div +]:=a[(len-i) div +]*+ord(s[i])-;
    len:=(len+) div ;
    for i:=len downto  do
    begin
        c[i]:=c[i]+a[i] div x;
        a[i-]:=a[i-]+(a[i] mod x)*;
    end;
    divide:='';
    for i:=len downto  do
    begin
        str(c[i],s);
        if c[i]< then divide:=divide+'';
        if c[i]< then divide:=divide+'';
        if c[i]< then divide:=divide+'';
        if c[i]< then divide:=divide+'';
        if c[i]< then divide:=divide+'';
        if c[i]< then divide:=divide+'';
        if c[i]< then divide:=divide+'';
        divide:=divide+s;
    end;
    while (divide[]='') and (length(divide)>) do delete(divide,,);
end;
 
procedure main;
var
    sum                        :int64;
    flag                    :boolean;
    cnt                        :int64;
    ans, s                    :ansistring;
    i, j                    :longint;    
 
begin
    if n= then
    begin
        if (d[]=) or (d[]=-) then writeln() else writeln();
        exit;
    end;
    sum:=;
    flag:=false;
    cnt:=;
    for i:= to n do if d[i]<>- then
    begin
        inc(sum,d[i]-);
        inc(cnt);
        if (d[i]>n-) or (d[i]=) then flag:=true;
    end;
 
    if flag then
    begin
        writeln();
        exit;
    end;
    if sum>n- then
    begin
        writeln();
        exit;
    end;
    flag:=false;
    ans:='';
    for i:=n--sum to n- do
    begin
        str(i,s);
        ans:=mul(ans,s);
    end;
    str(n-cnt,s);
    for i:= to n--sum do ans:=mul(ans,s);
    for i:= to n do
    begin
        if d[i]<>- then
            for j:= to d[i]- do
            begin
                ans:=divide(ans,j);
            end;
    end;
    writeln(ans);
end;
 
begin
    init;
    main;
end.