[TensorFlow]Tensor维度理解

http://wossoneri.github.io/2017/11/15/[Tensorflow]The-dimension-of-Tensor/

Tensor维度理解

Tensor在Tensorflow中是N维矩阵，所以涉及到Tensor的方法，也都是对矩阵的处理。由于是多维，在Tensorflow中Tensor的流动过程就涉及到升维降维，这篇就通过一些接口的使用，来体会Tensor的维度概念。以下是个人体会，有不准确的请指出。

tf.reduce_mean

reduce_mean(
    input_tensor,
    axis=None,
    keep_dims=False,
    name=None,
    reduction_indices=None
)

计算Tensor各个维度元素的均值。这个方法根据输入参数axis的维度上减少输入input_tensor的维度。

举个例子：

x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x)  # 1.5
tf.reduce_mean(x, 0)  # [1.5, 1.5]
tf.reduce_mean(x, 1)  # [1.,  2.]

x是二维数组[[1.0,1.0],[2.0, 2.0]]

当axis参数取默认值时，计算整个数组的均值：(1.+1.+2.+2.)/4=1.5

当axis取0，意味着对列取均值：[1.5, 1.5]

当axis取1，意味着对行取均值：[1.0, 2.0]

再换一个3*3的矩阵：

sess = tf.Session()
x = tf.constant([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]])
print(sess.run(x))
print(sess.run(tf.reduce_mean(x)))
print(sess.run(tf.reduce_mean(x, 0)))
print(sess.run(tf.reduce_mean(x, 1)))

输出结果是

[[ 1.  2.  3.]
 [ 4.  5.  6.]
 [ 7.  8.  9.]]
5.0
[ 4.  5.  6.]
[ 2.  5.  8.]

如果我再加一维是怎么计算的？

sess = tf.Session()
x = tf.constant([[[1., 1.], [2., 2.]], [[3., 3.], [4., 4.]]])
print(sess.run(x))
print(sess.run(tf.reduce_mean(x)))
print(sess.run(tf.reduce_mean(x, 0)))
print(sess.run(tf.reduce_mean(x, 1)))
print(sess.run(tf.reduce_mean(x, 2)))

我给的输入Tensor是三维数组：

[[[ 1.  1.]
  [ 2.  2.]]

 [[ 3.  3.]
  [ 4.  4.]]]

推测一下，前面二维的经过处理都变成一维的，也就是经历了一次降维，那么现在三维的或许应该变成二维。但现在多了一维，应该从哪个放向做计算呢？

看下结果：

2.5
[[ 2.  2.]
 [ 3.  3.]]
[[ 1.5  1.5]
 [ 3.5  3.5]]
[[ 1.  2.]
 [ 3.  4.]]

发现，

当axis参数取默认值时，依然计算整个数组的均值：(float)(1+2+3+4+1+2+3+4)/8=2.5

当axis取0，计算方式是：

[[(1+3)/2, (1+3)/2],
 [(2+4)/2, (2+4)/2]]

当axis取1，计算方式是：

[[(1+2)/2, (1+2)/2],
 [(3+4)/2, (3+4)/2]]

当axis取2，计算方式是：

[[(1+1)/2, (2+2)/2],
 [(3+3)/2, (4+4)/2]]

看到这里，能推断出怎么从四维降到三维吗？

有人总结了一下：

规律：

对于k维的，

tf.reduce_xyz(x, axis=k-1)的结果是对最里面一维所有元素进行求和。

tf.reduce_xyz(x, axis=k-2)是对倒数第二层里的向量对应的元素进行求和。

tf.reduce_xyz(x, axis=k-3)把倒数第三层的每个向量对应元素相加。

链接

拿上面的数组验证这个规律：

[[[ 1.  1.]
  [ 2.  2.]]

 [[ 3.  3.]
  [ 4.  4.]]]

我们的k=3。小括号是一层，在一层内进行计算：

axis=3-1=2，做最内层计算，我们的最内层就是(1,1),(2,2),(3,3),(4,4)，计算出来的就是

[[ 1.  2.]
 [ 3.  4.]]

axis=3-2=1，做倒数第二层计算(参考二维计算)：([1,1],[2,2])和([3, 3],[4, 4])

[[ 1.5  1.5]
 [ 3.5  3.5]]

axis=3-3=1，做倒数第三层计算:([[1, 1], [2, 2]])([[3, 3], [4, 4]])

[[ 2.  2.]
 [ 3.  3.]]

对于四维的，就贴段结果，自己可以尝试算一下，加深理解。

# input 4-D
[[[[ 1.  1.]
   [ 2.  2.]]

  [[ 3.  3.]
   [ 4.  4.]]]

 [[[ 5.  5.]
   [ 6.  6.]]

  [[ 7.  7.]
   [ 8.  8.]]]]
# axis=none
4.5

# axis=0
[[[ 3.  3.]
  [ 4.  4.]]

 [[ 5.  5.]
  [ 6.  6.]]]

# axis=1
[[[ 2.  2.]
  [ 3.  3.]]

 [[ 6.  6.]
  [ 7.  7.]]]

在tensorflow 1.0版本中，reduction_indices被改为了axis，在所有reduce_xxx系列操作中，都有reduction_indices这个参数，即沿某个方向，使用xxx方法，对input_tensor进行降维。

对于axis参数的作用，文档的解释是

the rank of the tensor is reduced by 1 for each entry in axis

即Tensor在axis的每一个分量上的秩减少1。如何理解矩阵的「秩」？ - 马同学的回答 - 知乎

附一张reduction_indices的图

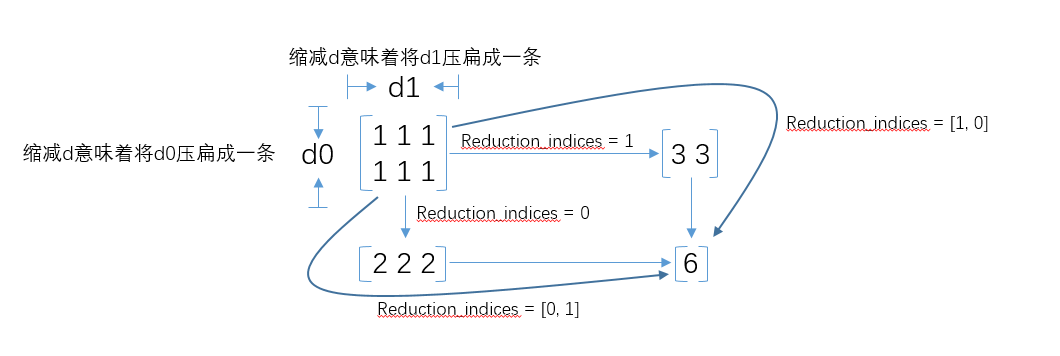
下面再看下第三个参数keep_dims，该参数缺省值是False，如果设置为True，那么减少的维度将被保留为长度为1。

回头看看最开始的例子：

# 2*2
[[ 1.  1.]
 [ 2.  2.]]
# keep_dims=False
[ 1.5  1.5]	# 1*2
[ 1.  2.]	#1*2
# keep_dims=True
[[ 1.5  1.5]]	#1*2
[[ 1.]			#2*1
 [ 2.]]

可以看到差别。关于这个参数，还没看到太多介绍，还需要了解。