cf div2 236 D

D. Upgrading Array

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You have an array of positive integers a[1], a[2], ..., a[n] and a set of bad prime numbers b1, b2, ..., bm. The prime numbers that do not occur in the set b are considered good. The beauty of array a is the sum 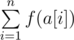, where function f(s) is determined as follows:

• f(1) = 0;
• Let's assume that p is the minimum prime divisor of s. If p is a good prime, then 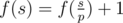, otherwise .

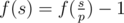You are allowed to perform an arbitrary (probably zero) number of operations to improve array a. The operation of improvement is the following sequence of actions:

• Choose some number r (1 ≤ r ≤ n) and calculate the value g = GCD(a[1], a[2], ..., a[r]).
• Apply the assignments: , , ..., .

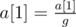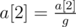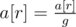What is the maximum beauty of the array you can get?

Input

The first line contains two integers n and m (1 ≤ n, m ≤ 5000) showing how many numbers are in the array and how many bad prime numbers there are.

The second line contains n space-separated integers a[1], a[2], ..., a[n] (1 ≤ a[i] ≤ 109) — array a. The third line contains m space-separated integers b1, b2, ..., bm (2 ≤ b1 < b2 < ... < bm ≤ 109) — the set of bad prime numbers.

Output

Print a single integer — the answer to the problem.

Sample test(s)

input

5 2
4 20 34 10 10
2 5

output

-2

input

4 5
2 4 8 16
3 5 7 11 17

output

10

贪心，从右往左扫gcd，若遇到好的质因子少于坏的质因子则可以更新使答案增加

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <cmath>
 #include <set>

 using namespace std;

 #define maxn 40005
 #define INF (1 << 30)

 bool prime[maxn];
 int ele[maxn],a[],g[],b[];
 int len = ,n,m,ans = ;

 int gcd(int x,int y) {
         return y ? gcd(y,x % y) : x;
 }

 int cal(int x) {
         int sum = ;
         for(int i = ; i * i <= x; ++i) {
                 if(x % i == ) {
                         int v,pos;
                         pos = lower_bound(b + ,b + m + ,i) - b;
                         v = b[pos] == i ? - : ;
                         while(x % i == ) {
                                 sum += v;
                                 x /= i;
                         }
                 }
         }

         if(x != ) {
                 int pos = lower_bound(b + ,b + m + ,x) - b;
                 sum += b[pos] == x ? - : ;
         }
         return sum;
 }

 void solve() {
         //printf("cal = %d\n",cal(4));
         for(int i = ; i <= n; ++i) {
                 ans += cal(a[i]);
         }

         g[] = a[];
         for(int i = ; i <= n; ++i) {
                 g[i] = gcd(g[i - ],a[i]);
         }

         int t = ;
         for(int i = n; i >= ; --i) {
                 int v;
                 if((v = cal(g[i] / t)) < ) {
                         //printf("g = %d v = %d\n",g[i],v);
                         ans += (-v) * i;
                         t *= g[i] / t;
                 }
         }

         printf("%d\n",ans);
 }
 int main() {

         //freopen("sw.in","r",stdin);

         scanf("%d%d",&n,&m);
         for(int i = ; i <= n; ++i) scanf("%d",&a[i]);
         for(int i = ; i <= m; ++i) {
                scanf("%d",&b[i]);
         }
         b[m + ] = INF;

         solve();
         return ;
 }