KMP算法中next函数的理解

首先要感谢http://blog.csdn.net/v_july_v/article/details/7041827以及http://blog.chinaunix.net/uid-27164517-id-3280128.html两篇博文的作者，参考这两篇博文才对KMP算法有了初步认识，本文的一些内容也是来自于这两篇之中。KMP算法与BF算法的优略、回溯不回溯这些问题本文不作说明，而主要说明next函数（通常保存为一个next数组）的意义。这正是KMP算法难于理解的地方。

　　为了方便起见，在不会起歧义的情况下做如下约定：下标都从0开始; 假设字符串为S，那么S_i 表示第i个字符或者只有第i个字符的字符串；S_iS_i+1S_i+2表示子串，如S₁S₂S₃，S₄S₅等等；pre(S,i)表示字符串S的位置i之前的字符串，即S₀S₁...S_i-1；next函数和next数组表示同一个意思。本文分为两节，第一节讲next函数的意义，得出需要满足的两个条件；第二节是具体代码以及相关说明。

第一节  next函数的意义

我们知道，KMP的基本匹配过程如下：在字符串T中查找模式P，需要记录T中的当前位置i 以及P中的当前位置 j。当T_i=P_j的时候i和j都自增；当T_i!=P_j时，令j=next(j)，然后继续匹配。这样就跳过了一些字符，而这些字符，本质上来讲与字符串P₀P_1...P_j-1的前缀和后缀能匹配的最大长度相关。以图一作解释，来倒推next(j)的意义：

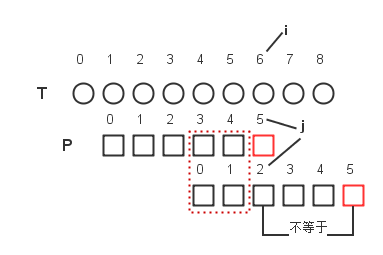
图 1

在T中查找P，P₀P₁P₂P₃P₄=T₁T₂T₃T₄T₅，但P₅!=T₆（i=6,j=5）。此时令j=next(j)。假设next[5]=2, 则跳过三个字符，新的j=2，从这个位置开始比较。能跳过的条件是什么？其一，从虚线部分可知必须保证P₀P₁=P₃P₄；其二，P₅不能等于P2，因为之前我们知道了P₅!=T₆，如果P₅=P₂，那么P₂肯定不等于T_6。再次强调观察虚线部分，发现P₀P₁和P₃P₄正好是字符P₅前面的字符串（即P₀P₁P₂P₃P_4）的前缀和后缀。

    图1中，P₅！=T₆时跳过了三个字符，next[5]=2。再看图2：next(5)分别等于4,3,1,0的情况。

图 2

仔细观察图2中的四种情况，均需要符合上面所说的条件。对于图2的最后一幅图，此种情况的条件是P₀P₁P₂P₃P₄没有相等的前缀和后缀，且P₀!=P_5。那么如果后一个条件不满足呢，那么显然P应该再移一个位置，对应的情况如图3：

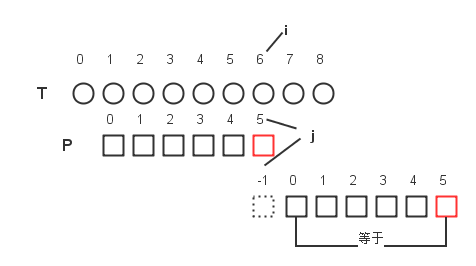
图 3

图3中，next(5)=-1。因此next=-1的情况：P_j=P₀，且P₀P_1...P_j-1没有任何相等的前缀和后缀。另外，一般地，如果P₀就发生失配，那么显然i也要加一，因此next(0)=-1。

在此作一小结，k=next(j)需要满足的两个条件如下：

条件1. k是P₀P_1...P_j-1最长匹配的前缀和后缀的长度.

    条件2. P_j!=P_k.

第二节  next函数的求法

利用以上知识，我们就知道求next函数的思路了。基本思路是利用上面的第一个条件（寻找最长匹配的前后缀），而第二个条件（P_j!=P_next(j)）则作为优化。这样一步步理解会对算法思路更清晰一点。

基本思路: 利用条件1

使用归纳法:假设next(j)=k，则P₀P₁...P_k-1=P_j-k...P_j-2P_j-1，那么next(j+1)有两种情况:

1. 如果P_k=P_j，则P₀P₁...P_k=P_j-k...P_j-1P_j，所以next(j+1)=k+1=next(j)+1。

2. 如果P_k!=P_j，这是可以看做另外一个字符串匹配的问题，主串和模式串都是p，当匹配失败时，k=next(k)。

因此得到如下算法：

void get_nextval(char const* ptrn, int plen, int* nextval)
{
    int i = 0;
    nextval[i] = -1;
    int j = -1;
    while( i < plen-1 )
    {
        if( j == -1 || ptrn[i] == ptrn[j] )   //对应情况1
        {
            ++i;
            ++j;
            next(i)=j;
        }
        else                                  //对应情况2
            j = nextval[j];
    }
}  　

上述算法中，ptrn是模式串，plen是模式串长度，nextval数组保存所有位置的next值。该算法不考虑条件2，因此有可能发生P_i=P_next(i)这种情况。在缺少该条件的情况下也可以用于做字符串匹配。假设next(i)=k，当匹配到i失效时，i=next(i)=k，这时候肯定也失效，因此又寻找k对应的next值，这样算法得以进行。

优化：利用条件2

比较常见的算法对情况1做了优化，如下:

 void get_nextval(char const* ptrn, int plen, int* nextval)
 {
     int i = ;
     nextval[i] = -;
     int j = -;
     while( i < plen- )
     {
         if( j == - || ptrn[i] == ptrn[j] )   //对应情况1
         {
             ++i;
             ++j;
             if( ptrn[i] != ptrn[j] )
                 nextval[i] = j;
             else
                 nextval[i] = nextval[j];
         }
         else                                  //对应情况2
             j = nextval[j];
     }
 }

　　该版本的算法考虑了条件2，因此进入情况1的时候，next(i)!=j。我们可以考虑一条查询链，如图4：

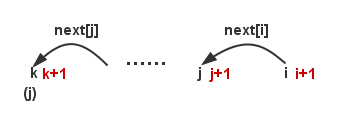
    图4

假设现在刚刚运行完13行，得出next[i]=j。此时必然有ptrn[i]!=ptrn[j]。因此下个循环的时候会跳转到18行。该next链一直往前搜寻，直到某个位置k，ptrn[k]与ptrn[i]相等。该k就是最新的j值，这样回到情况1，接着按照条件1优化。另外，当j==-1也应当进入情况1，因为不能往前搜寻了。

以上就是next数组的求解过程，往后就可以利用next数组进行字符串查找了。在写查找算法的过程中，可以发现与求next数组的算法过程惊人的一致。这也是KMP算法的一个特点，把两者结合起来，更能够理解它的奥妙所在。