图解论文《The Part-Time Parliament》

本文以图文并茂的方式重新演绎 Paxos 开山之作 《The Part-Time Parliament》[1]，并尝试解释原论文中语焉不详的地方。

背景

在 Paxos 小岛上，施行着一种 Parliament(议会) 政治。小岛上执行的所有 decree(法令) 都需要先由 Parliament 在 Chamber 内表决通过。legislator(议员) 将 Parliament 通过的 decree 记录在他随身携带的 ledger(账本) 上。比如某 legislator 在其 ledger 记录了第 155 号 decree 如下：

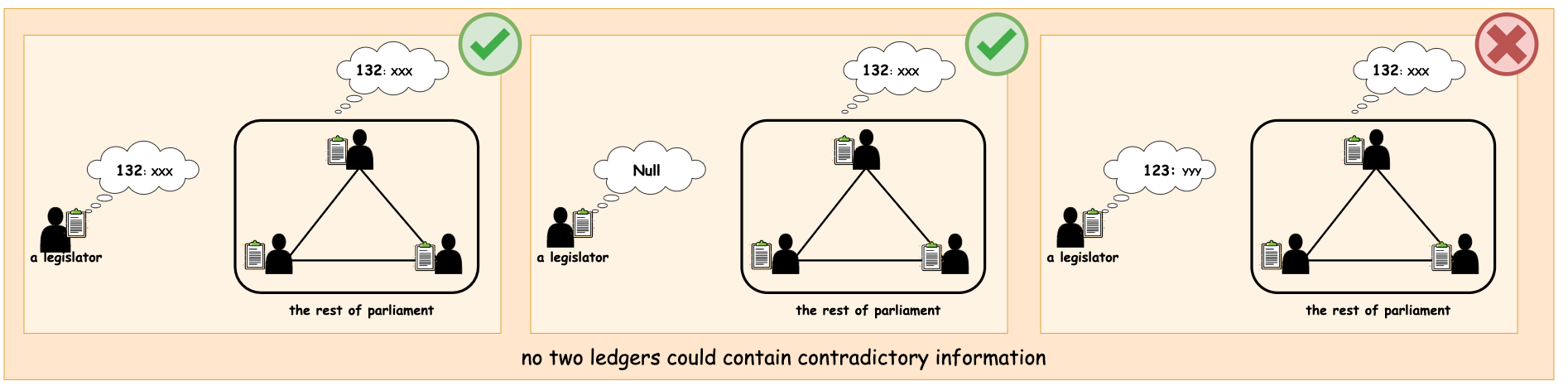
为了防止岛上的 decree 出现冲突，导致不必要的纠纷, 任何两个 legislator 记录的相同编号的 decree 要么是一样的，要么其中某个 legislator 不存在该编号的 decree。

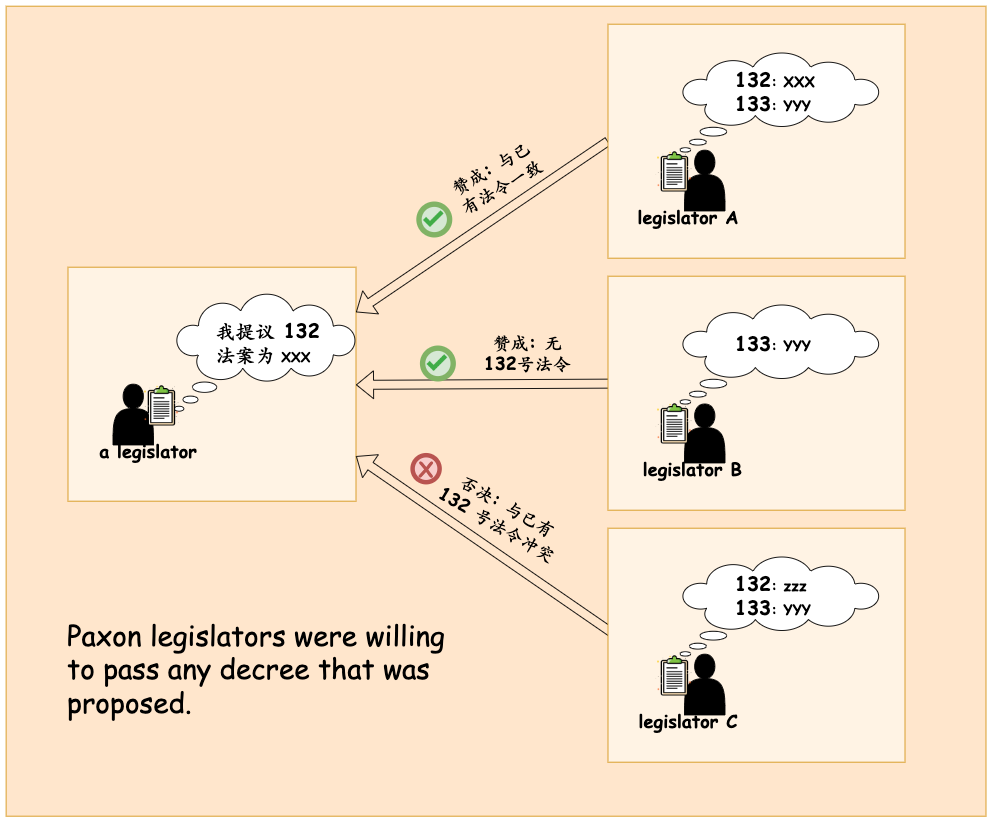
legislator 倾向于通过别人发起的 decree 请求, 只要其他 legislator 发起的 decree 请求与自己 ledger 记录不冲突，则为它投票。

为了保证 decree 的顺利产生， 除了在 ledger 正面记录表决通过的 decree, legislator 还需要记录一些中间过程: 需要长期持有的信息记录在 ledger 背面, 这部分信息可以被划掉；需要临时持有的信息记录在草稿纸上, legislator 仅在 Chamber 内保留记录信息的草稿纸。

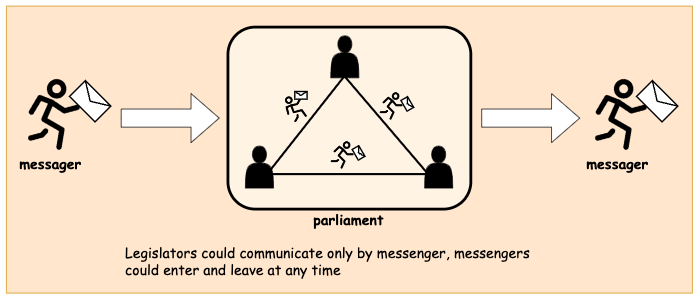
legislator 都是兼职的(part-time), 因此他们可以选择随时离开或加入 Chamber 参与投票。

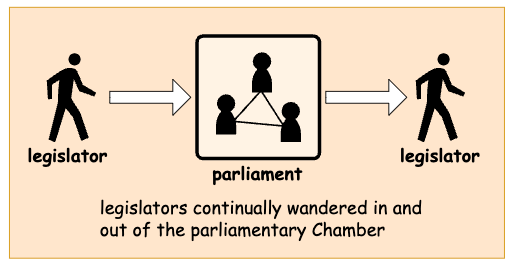
由于 Chamber 内人员众多，比较嘈杂，legislator 之间通过只能通过信使(messager)进行交流。信使同样也是兼职的，他们和 legislator 一样，可以随时选择进入或离开 Chamber(即使他正在参与某次消息的传递。这将导致这条消息永远消失，或者这条消息会在不可预见的未来重新参与传递)。

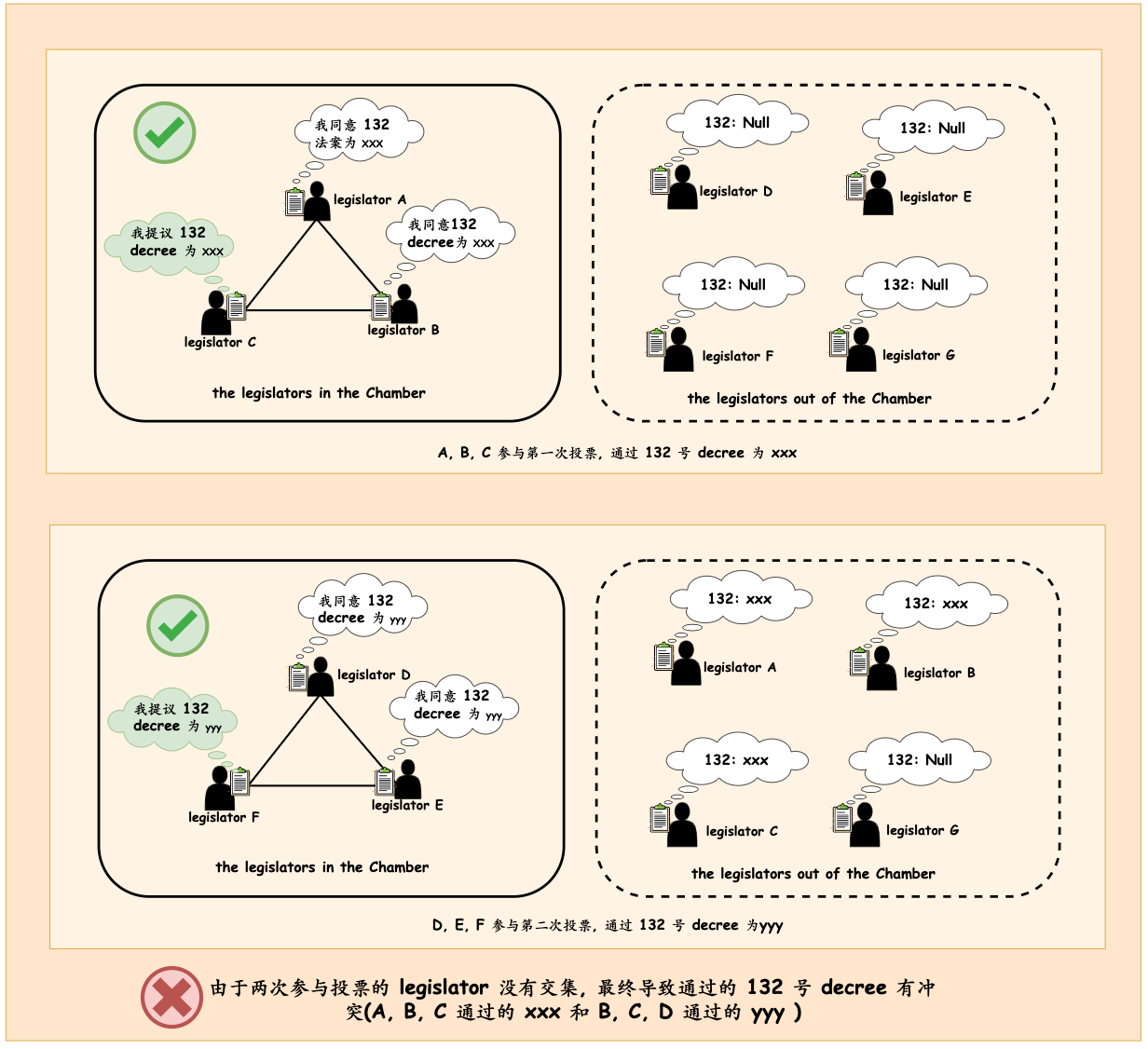
Chamber 内 legislator 进进出出有个比较严重的问题： 两次参会的人如果没有交集， 他们可能会投票产生互相冲突的提案，这将导致 legislator 记录的相同编号 decree 产生冲突，不能满足一开始对 decree 的约束。(任何两个 legislator 记录的相同编号的 decree 要么是一样的，要么其中某个 legislator 不存在该编号的 decree)

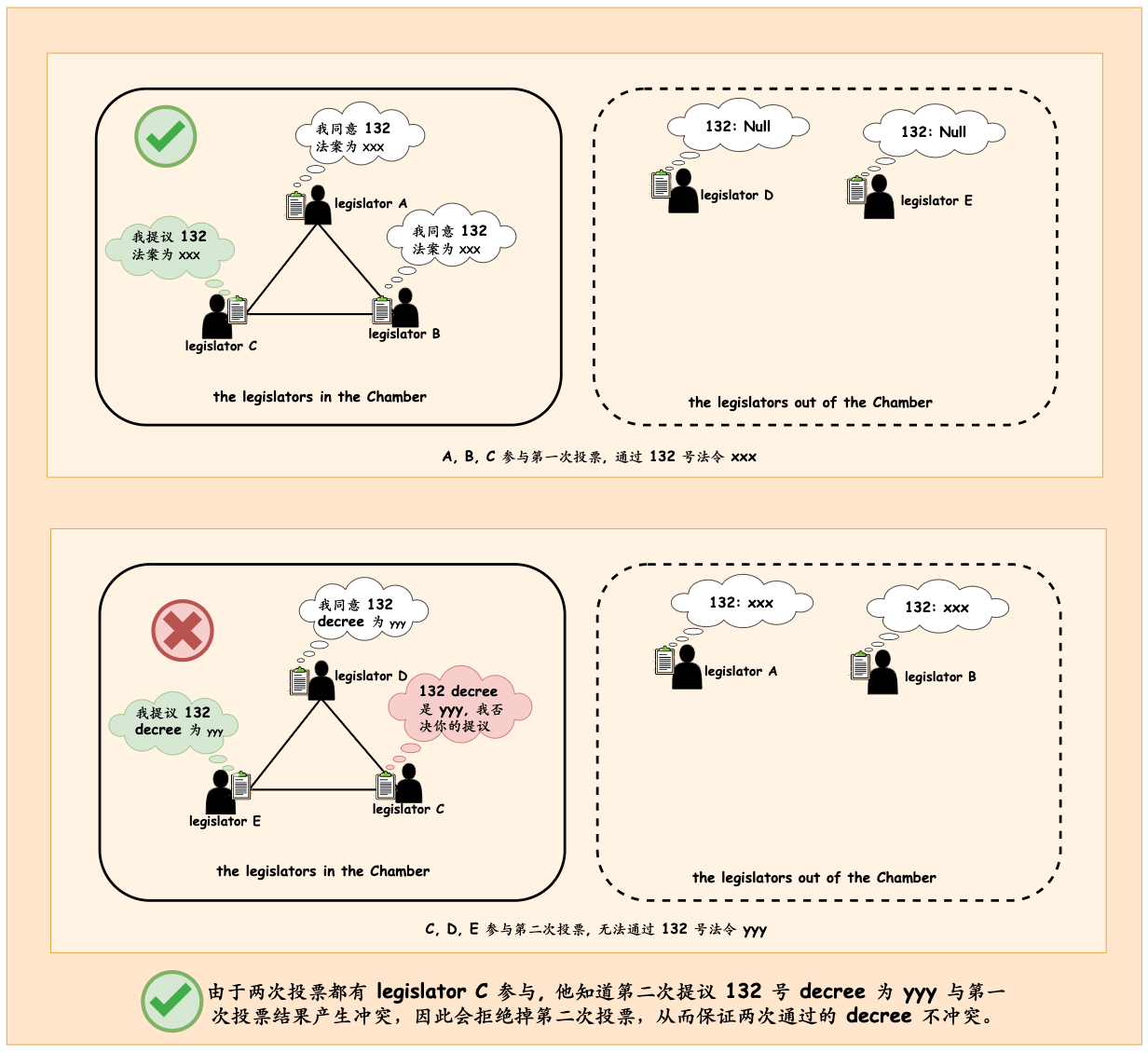
为了解决这个问题，Paxos 小岛上的人对 与会人数(Quorum) 进行了约束：当与会人数占 legislator 总人数的一半以上时，才能发起提案流程，否则，法案无法通过。根据鸽巢原理，两次投票至少有一个 legislator 都有参与，他将会拒绝冲突的提案内容形成 decree。

当与会的所有 legislator 都投票表示赞成(意味着与历史 decree 无冲突)， 提议的已通过成为 decree， 周知到所有与会人员，记录在 ledger 证明正式生效。

The Single-Decree Synod

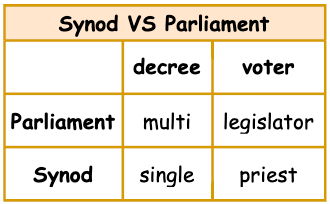
上一部分介绍了 paxos 小岛上的 Parliament 将 decree 从提出到通过的整体流程。在 Parliament 中可以通过很多 decree， 本节为了探索 decree 达成共识的具体细节，先从达成单个 decree 的 Synod 会议聊起。Synod 和 Parliament 的差异如下：

在 Synod 会议中，每个 Priest 可以参与多轮 投票(Ballot)。每位 priest 每轮 ballot 仅能投一次票。 ballot B 包含一下四种信息:

• B_dec: 本轮 ballot 提议待通过的 decree;
• B_qrm: 与会的 priest 的集合;
• B_vot: 已参与投票的 priest 的集合;
• B_bal: 本轮 ballot 的编号, 全序。(注意与 decree 编号区分)
  
  

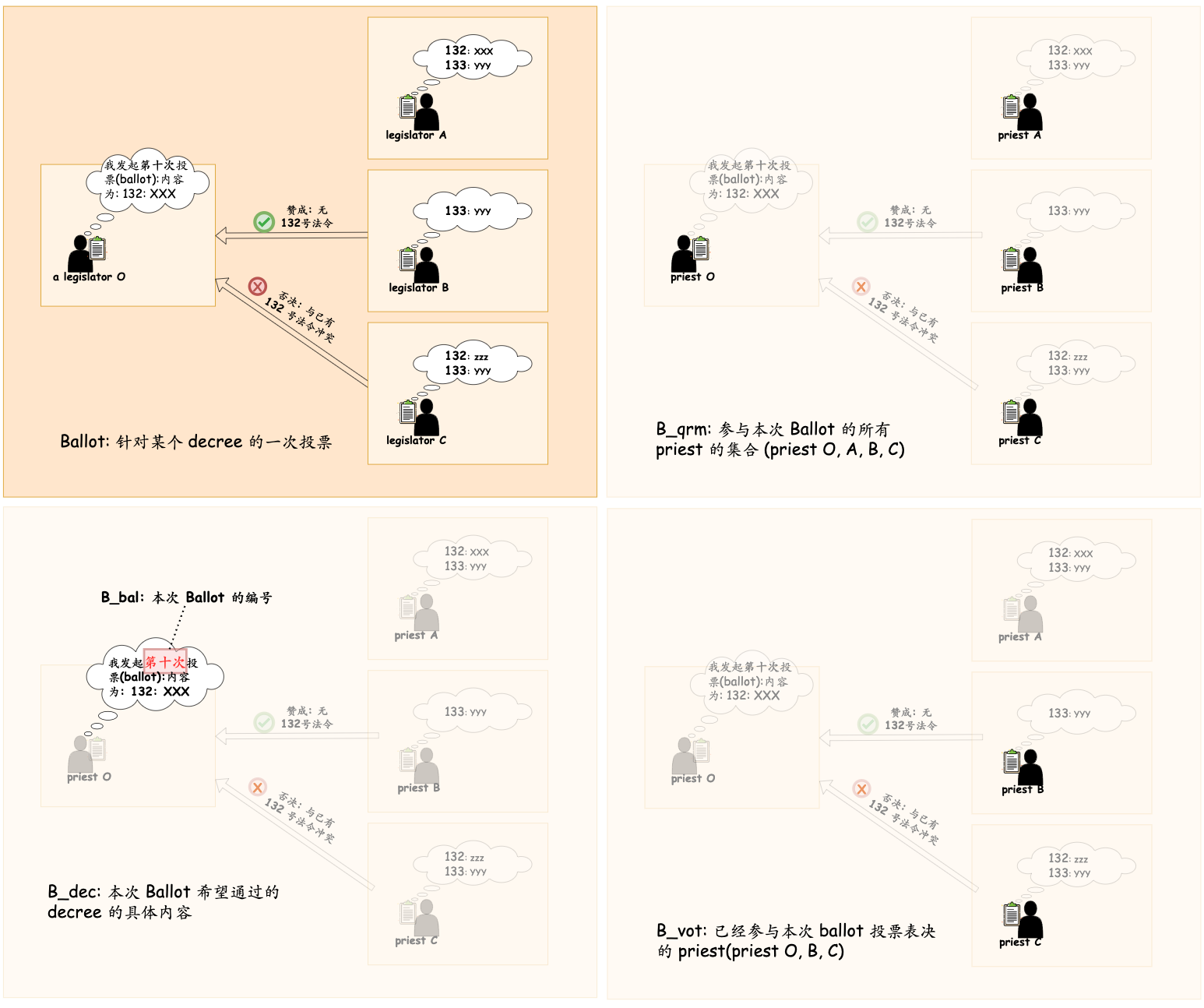
根据第一部分的铺垫，我们知道当且仅当 B_vot 是 B_qrm 的子集，即所有与会的 priest 都已参与投票，这次 ballot 才是成功的(本轮 ballot 提议的 decree 通过)。

为了保证 Synod 会议最终最多产生唯一 decree(无冲突), 我们需要保证以下三点条件:

• B1: 为了标识 ballot，每一轮 ballot 需要有唯一的编号。
• B2: 任意两轮 bollot 至少保证有一个 priest 同时参与。(第一部分已经解释过这么做的原因)
• B3 : 如果某些 priest 在之前的 ballot 已经参与过投票，则本轮 ballot 投票的 decree 等于他们参与的最近一次 ballot 的 decree。

比如，在 Fig. 1 [1] 中, 展示了五轮 ballot(ballot 编号分别为 2, 5, 14, 27, 29)。 Synod 共有五位 priest: A, B, Γ，Δ 和 E。 每轮 ballot 罗列出来的 priest 就是本轮与会的 Quorum。用矩形框框出的 priest 代表本轮已参与投票的 priest。依次解释每轮 ballot 的内容如下：

• 2: 最早的 ballot，可以投票任何 decree。 本轮提议 decree α， Δ 已为它投票。
• 5: 参与本轮 ballot 的 A, B, Γ 和 E 都没有参与更早的投票，因此他们都可以为本轮提议 decree β 投票。本轮仅 Γ 参与了投票。
• 14: 本轮 ballot 中, Δ 已经为 decree α 投过票(ballot 2 中)，因此本轮 decree 只能为 α。本轮 B, E 已经投票。
• 27: 本轮 ballot 中， Δ 已经为 decree α 投过票(ballot 2 中, 注意 Δ 未参与 ballot 14 的投票)， Γ 已经为 decree β 投过票(ballot 5 中)。因此本轮 decree 必须与 ballot 5(max(2, 5)) 相同，即 decree β。本轮与会的 A, Γ，Δ 都已参与投票，本轮 ballot 成功通过了 decree β。
• 29: 参与本轮 ballot 的 priest 中，B 参与的最新一次投票为 ballot 14， Γ，Δ 参与的最新一次投票为 ballot 27， 因此本轮 ballot 的 decree 必须和 ballot 27(max(14, 27) ) 一致，即 decree β。本轮仅 B 完成了投票。

某轮 ballot B 一旦投票成功，参与后续 ballot 的 priest 至少有一位曾参与 B 的投票(B2)，根据 B3, 后续 ballot 投票的 decree 必须保持和 ballot B 一致。因此， 后续通过的所有 decree 都必须和第一次通过的 decree 内容保持一致。

为了满足 B1 的需求，将 Bollot 编号设为 <priest id, ballot id> 格式, 其中 priest id 表示发起该 Ballot 的 priest 的编号。同一个 priest 不会发起编号相同的 Ballot， 因此能满足 Ballot 编号不冲突的要求。

在第一部分已经讨论，为了满足 B2，只需要保证每次参与投票的 priest 人数占总人数的一半以上，根据鸽巢原理，任意两轮 bollot 至少保证有一个 priest 同时参与。

要满足 B3 的要求相对麻烦一些。保证 B3 的关键在于 Ballot 编号小于当前正在处理的 Ballot 的集合不再变动(否则无法拿到最新的“本轮 ballot 投票的 decree 等于他们参与的最近一次 ballot 的 decree”。)。

为了保证“ Ballot 编号小于当前正在处理的 Ballot 的集合不再变动”， 借鉴两阶段提交策略，将请求拆分为两部分：第一部分向 B_qrm 的 priest 申请处理当前 Ballot(编号为 B_bal)，并且要求他们保证不再处理 “Ballot 编号小于当前正在处理的 Ballot”；第二部分才向 B_qrm 实际发起本轮 Ballot 的数据请求。

实现细节见下图：

The Multi-Decree Parliament

The Multi-Decree Parliament 算法实际上是对每个带有编号的 decree 执行 The Single-Decree Synod 算法，最终实现一系列 decree 都能达成一致。

参考文献

[0] 本文所有绘图均使用 draw.io 绘制

[1] The Part-Time Parliament