JZOJ 4895【NOIP2016提高A组集训第16场11.15】三部曲

题目

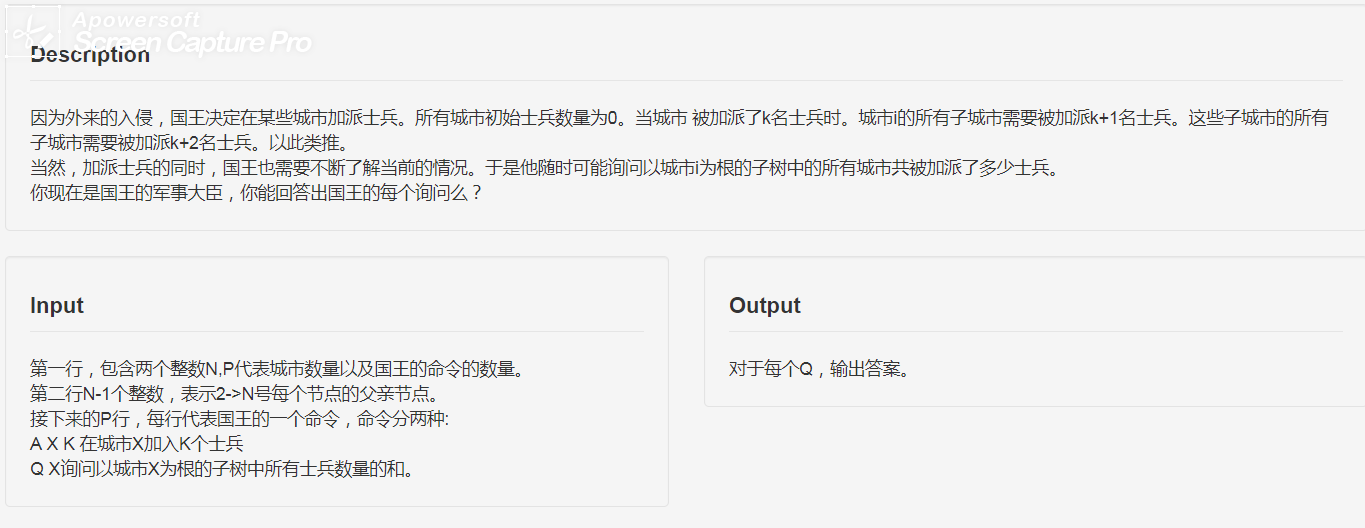
对于 \(50%\) 的数据，\(1<=n<=1000,1<=p<=300\)

对于 \(100%\) 的数据，\(1<=n<=50000,1<=p<=100000,1<=x<=n,0<=k<=1000\)

分析

树上子树加的操作让我们联想到线段树的区间加

然后我们就可以用 \(dfs\) 序把子树弄到序列里

于是考虑怎么加

记根节点深度为 \(0\)

那么让整个子树加 \(k-dep_x\)，再有的贡献就是一个节点的深度乘上被加的次数

于是线段树维护即可

\(Code\)

#include<cstdio>
#define LL long long
#define ls (k << 1)
#define rs (ls | 1)
using namespace std;

const int N = 5e4 + 5;
int n , p , dfc , tot , dfn[N] , dep[N] , siz[N] , h[N] , rev[N];
LL d[N] , sum[N * 4] , tag_s[N * 4] , tag_c[N * 4];
struct edge{
	int to , nxt;
}e[N];

inline void add(int x , int y){e[++tot] = edge{y , h[x]} , h[x] = tot;}

void dfs(int x)
{
	dfn[x] = ++dfc , rev[dfc] = x , siz[x] = 1;
	for(register int i = h[x]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		dep[v] = dep[x] + 1;
		dfs(v);
		siz[x] += siz[v];
	}
}

void pushdown(int l , int r , int k)
{
	if (tag_s[k] == 0 && tag_c[k] == 0) return;
	int mid = (l + r) >> 1;
	sum[ls] += tag_s[k] * (mid - l + 1) + tag_c[k] * (d[mid] - d[l - 1]);
	tag_s[ls] += tag_s[k] , tag_c[ls] += tag_c[k];
	sum[rs] += tag_s[k] * (r - mid) + tag_c[k] * (d[r] - d[mid]);
	tag_s[rs] += tag_s[k] , tag_c[rs] += tag_c[k];
	tag_s[k] = tag_c[k] = 0;
}

void update(int l , int r , int k , int tl , int tr , int v)
{
	if (tl <= l && r <= tr)
	{
		sum[k] += 1LL * (r - l + 1) * v + (d[r] - d[l - 1]);
		tag_s[k] += v , tag_c[k] += 1;
		return;
	}
	pushdown(l , r , k);
	int mid = (l + r) >> 1;
	if (tl <= mid) update(l , mid , ls , tl , tr , v);
	if (tr > mid) update(mid + 1 , r , rs , tl , tr , v);
	sum[k] = sum[ls] + sum[rs];
}

LL query(int l , int r , int k , int tl , int tr)
{
	if (tl <= l && r <= tr) return sum[k];
	pushdown(l , r , k);
	int mid = (l + r) >> 1;
	LL res = 0;
	if (tl <= mid) res += query(l , mid , ls , tl , tr);
	if (tr > mid) res += query(mid + 1 , r , rs , tl , tr);
	return res;
}

int main()
{
	freopen("truetears.in" , "r" , stdin);
	freopen("truetears.out" , "w" , stdout);
	scanf("%d%d" , &n , &p);
	int x , y;
	for(register int i = 2; i <= n; i++) scanf("%d" , &x) , add(x , i);
	dfs(1);
	for(register int i = 1; i <= dfc; i++) d[i] = d[i - 1] + dep[rev[i]];
	char opt[5];
	for(register int i = 1; i <= p; i++)
	{
		scanf("%s" , opt);
		if (opt[0] == 'A')
		{
			scanf("%d%d" , &x , &y);
			update(1 , n , 1 , dfn[x] , dfn[x] + siz[x] - 1 , y - dep[x]);
		}
		else {
			scanf("%d" , &x);
			printf("%lld\n" , query(1 , n , 1 , dfn[x] , dfn[x] + siz[x] - 1));
		}
	}
}