【题解】C2Crni - Crni [COCI2010] [SP7884]

传送门：\(\text{C2Crni - Crni}\) \(\text{[COCI2010]}\) \(\text{[SP7884]}\)

【题目描述】

给定一个 \(\text{N} * \text{N}\) 的矩阵，每个格子要么为白色（\(B\)）要么为黑色（\(C\)）。定义黑矩形为所含单元格数大于等于 \(2\) 且所含单元格均为黑色的矩阵。

如图：

左边的两个矩形都不是黑矩形，因为 \(1\) 中有白格，\(2\) 的大小为 \(1\)，而右图的 \(3\) 个都是黑矩形。

要解决的问题是在给定的矩形中找出两个没有共公部分的黑矩形，输出所有方案数，由于数较大，答案对 \(10007\) 取模。

【样例】

样例输入：

2

CC

CC

样例输出：

2

样例输入：

3

CCB

CCB

CBB

样例输出：

5

样例输入：

5

BCCBB

BBCBB

BCCBB

BBBBB

CCBBB

样例输出：

8

【数据范围】

\(100 \%:\) \(1 \leqslant n \leqslant 1000\)

【分析】

这是一道套路题，用到了很多关于矩阵的处理技巧，但找到解决方法后会发现它的思维难度其实并不高，主要是代码实现较困难，所以也可以视其为膜你题。

【前缀和的套路】

找子矩阵基本都会用到前缀和，常见的查询子矩阵可以直接容斥，例如维护二维树状数组时用到的方法：

设 \(S[x][y]=\sum_{i=1}^{x} \sum_{j=1}^{y} a[i][j]\)，那么递推式为 \(S[i][j]=\) \(S[i-1][j]+S[i][j-1]-S[i-1][j-1]+a[i][j]\)

如果要查询以 \((x1,y1)\) 为左下角，以 \((x2,y2)\) 为右下角的矩阵和，\(\sum_{i={x_1}}^{y_1} \sum_{j={x_2}}^{y_2} a[i][j]=\) \(S[x2][y2]-S[x1-1][y2]-S[x2][y1-1]+S[x1-1][y1-1]\)

在预处理式子时需要从左上角一直递推到右下角，而稍复杂一点的需要统计多个方向（没错，就是此题了），即从最多 \(4\) 个角落（左上，左下，右上，右下）开始向其对角处递推，得到多个助于统计答案的前缀和数组。

【预处理】

回到此题。

为方便处理，将矩阵中的黑点设为 \(1\)，白点设为 \(0\) 。

对于所有的黑点，先预处理出 \(4\) 个数组：

\((1).\) \(RD[i][j]\)：以 \((i,j)\) 为右下角的黑矩阵个数。

\((2).\) \(LU[i][j]\)：以 \((i,j)\) 为左上角的黑矩阵个数。

\((3).\) \(LD[i][j]\)：以 \((i,j)\) 为左下角的黑矩阵个数。

\((4).\) \(RU[i][j]\)：以 \((i,j)\) 为右上角的黑矩阵个数。

但如果暴力枚举的话 \(O(n^4)\) 复杂度过高，需要考虑合理继承前面求出的信息。

以 \(RD\) 为例，为便于推导，我们先在矩阵中枚举一条辅助线，假设已经求出了第 \(i\) 行前 \(j-1\) 列的 \(RD\) 信息，如图为 \(i=4,j=4\) 的情况：

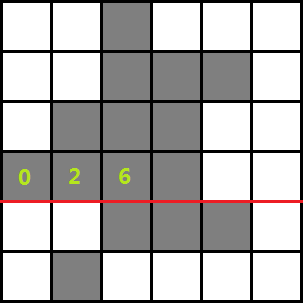
定义 \(H[i][j]\) 为点 \((i,j)\) 向上最多可以延伸的距离（或者说高度），如果 \(a(i,j)\) 为白块，\(H[i][j]=0\) 。

处理方法如下：

对于点 \((i,j)\) 找到同一列前面第一个 \(H\) 小于它的位置 \((i,k)\)。

由于 \([k+1,j]\) 的高度都大于 \(j\)，那么将会有 \(H[i][j]*(j-k)\) 个点可以作为黑矩形的左上角（右下角为 \((i,j)\)），但是将 \((i,j)\) 自己作为左上角时黑矩阵大小只有 \(1\)，所以要减去 \(1\) 。

另外以 \((i,k)\) 为右下角的黑矩阵都可以将长度扩大 \(j-k\)，即变成以 \((i,j)\) 为右下角，但以 \((i,k)\) 为右下角的情况没有计算在 \(RD[i][k]\) 以内，所以要加上 \(1\) 。

得到递推式为：\(RD[i][j]=H[i][j]*(j-k)-1+RD[i][k]+1\) 。

于是时间复杂度就被优化到了 \(O(n^3)\)，但还不够优秀。

现在的问题是如何快速找 \(k\)，方法同 \(\text{Largest}\) \(\text{Rectangle}\) \(\text{in}\) \(\text{a}\) \(\text{Histogram}\) （题解），直接单调栈维护即可。

在上面那张图中 \(H[4][1]=1,H[4][2]=2,H[4][3]=4,H[4][4]=3\)，所以 \(j=4\) 时的决策点 \(k=2\)，因此 \(RD[3][4]=3*2-1+RD[3][2]+1\) 。

同理可得 \(LU,LD,RU\) 。

【统计答案】

依旧是枚举辅助线：

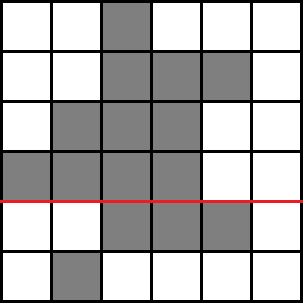
先求出下边界在红线上面的黑矩形个数，即 \(\sum_{i=1}^{x} \sum_{j=1}^{n} RD[i][j]\)（或者 \(LD[i][j]\)），

再求出上边界紧贴在红线下面的黑矩阵个数，即 \(\sum_{j=1}^{n}LU[x+1][j]\)（或者 \(RU[x+1][j]\)），

将二者相乘，再对于每一条辅助线算出的结果求和，得到相对位置为上下的黑矩形总对数。（其实也可以固定红线上面，红线下面求总个数）

同理枚举竖线，可得相对位置为左右的黑矩形总对数。

但这样会有算重复的情况，如下图绿色部分和蓝色部分：

因此还要减去相对位置既有上下又有左右的黑矩形对数，也就是在十字线对角象限的黑矩形对数，求法和前面大致相同。为方便处理，要任选两个方向计算矩阵前缀和（递推式和二维树状数组的一样）：

\((1).\) \(S_{RD}[x][y]=\sum_{i=1}^{x} \sum_{j=1}^{y} RD[i][j]\)

前缀和递推方向：左上 \(\text{→}\) 右下。

矩阵前缀和意义：右下角在 \((i,j)\) 左上面的黑矩阵个数。

\((2).\) \(S_{LU}[x][y]=\sum_{i=n}^{x} \sum_{j=n}^{y} RD[i][j]\)

前缀和递推方向：右下 \(\text{→}\) 左上。

矩阵前缀和意义：左上角在 \((i,j)\) 右下面的黑矩阵个数。

\((3).\) \(S_{LD}[x][y]=\sum_{i=1}^{x} \sum_{j=n}^{y} RD[i][j]\)

前缀和递推方向：右上 \(\text{→}\) 左下。

矩阵前缀和意义：左下角在 \((i,j)\) 右上面的黑矩阵个数。

\((4).\) \(S_{RU}[x][y]=\sum_{i=n}^{x} \sum_{j=1}^{y} RD[i][j]\)

前缀和递推方向：左下 \(\text{→}\) 右上。

矩阵前缀和意义：右上角在 \((i,j)\) 左下面的黑矩阵个数。

最后，此题细节较多，变量名没设好的话很容易搞混。

时间复杂度为：\(O(n^2)\) 。

【Code】

#include<algorithm>

#include<iostream>

#include<cstring>

#include<cstdlib>

#include<cstdio>

#define Re register int

#define For(i,a,b) for(Re i=a;i<=b;++i)

#define Por(i,a,b) for(Re i=a;i>=b;--i)

#define print() for(Re i=1;i<=n;puts(""),++i)for(Re j=1;j<=n;++j)

using namespace std;

const int N=1003,P=10007;

int n,Q[N],A[N][N],H[N][N],SS[N][N];char ch[N];

inline void in(Re &x){

    int f=0;x=0;char c=getchar();

    while(c<'0'||c>'9')f|=c=='-',c=getchar();

    while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();

    x=f?-x:x;

}

int RD[N][N];

inline void get_RD(){//RD[i][j]: 以i,j为右下角的黑矩形个数(1,1)→(n,n)

    memset(H,0,sizeof(H));

    For(i,1,n)For(j,1,n)if(A[i][j])H[i][j]=H[i-1][j]+1;

//  print()printf("%d ",H[i][j]);puts("");

    For(i,1,n){

    	Re h=1,t=0;

    	For(j,1,n)if(!A[i][j])RD[i][j]=-1;

    	RD[i][Q[++t]=0]=-1;

    	For(j,1,n){

            while(h<=t&&H[i][Q[t]]>=H[i][j])--t;

            if(h<=t&&A[i][j])RD[i][j]=RD[i][Q[t]]+1+H[i][j]*(j-Q[t])-1;

            Q[++t]=j;

    	}

    	For(j,1,n)if(RD[i][j]<0)RD[i][j]=0;

    }

//  print()printf("%d ",RD[i][j]);puts("");

}

int LU[N][N];

inline void get_LU(){//LU[i][j]: 以i,j为左上角的黑矩形个数(n,n)→(1,1)

    memset(H,0,sizeof(H));

    Por(i,n,1)Por(j,n,1)if(A[i][j])H[i][j]=H[i+1][j]+1;

//  print()printf("%d ",H[i][j]);puts("");

    Por(i,n,1){

    	Re h=1,t=0;

    	Por(j,n,1)if(!A[i][j])LU[i][j]=-1;

    	LU[i][Q[++t]=n+1]=-1;

    	Por(j,n,1){

            while(h<=t&&H[i][Q[t]]>=H[i][j])--t;

            if(h<=t&&A[i][j])LU[i][j]=LU[i][Q[t]]+1+H[i][j]*(Q[t]-j)-1;

            Q[++t]=j;

    	}

    	Por(j,n,1)if(LU[i][j]<0)LU[i][j]=0;

    }

//  print()printf("%d ",LU[i][j]);puts("");

}

int LD[N][N];

inline void get_LD(){//LD[i][j]: 以i,j为左下角的黑矩形个数(1,n)→(n,1)

    memset(H,0,sizeof(H));

    For(i,1,n)Por(j,n,1)if(A[i][j])H[i][j]=H[i-1][j]+1;

//  print()printf("%d ",H[i][j]);puts("");

    For(i,1,n){

    	Re h=1,t=0;

    	Por(j,n,1)if(!A[i][j])LD[i][j]=-1;

    	LD[i][Q[++t]=n+1]=-1;

    	Por(j,n,1){

            while(h<=t&&H[i][Q[t]]>=H[i][j])--t;

            if(h<=t&&A[i][j])LD[i][j]=LD[i][Q[t]]+1+H[i][j]*(Q[t]-j)-1;

            Q[++t]=j;

    	}

    	Por(j,n,1)if(LD[i][j]<0)LD[i][j]=0;

    }

//  print()printf("%d ",LD[i][j]);puts("");

}

int RU[N][N];

inline void get_RU(){//RU[i][j]: 以i,j为右上角的黑矩形个数(n,1)→(1,n)

    memset(H,0,sizeof(H));

    Por(i,n,1)Por(j,n,1)if(A[i][j])H[i][j]=H[i+1][j]+1;

//  print()printf("%d ",H[i][j]);puts("");

    Por(i,n,1){

    	Re h=1,t=0;

    	For(j,1,n)if(!A[i][j])RU[i][j]=-1;

    	RU[i][Q[++t]=0]=-1;

    	For(j,1,n){

            while(h<=t&&H[i][Q[t]]>=H[i][j])--t;

            if(h<=t&&A[i][j])RU[i][j]=RU[i][Q[t]]+1+H[i][j]*(j-Q[t])-1;

            Q[++t]=j;

    	}

    	For(j,1,n)if(RU[i][j]<0)RU[i][j]=0;

    }

//  print()printf("%d ",RU[i][j]);puts("");

}

inline int U_D(){//加上-下

    Re ans=0,S=0;

    For(i,1,n){

    	For(j,1,n)(ans+=S*LU[i][j]%P)%=P;//用【左上角为(i,j)的矩阵LU】固定在辅助线下面

    	For(j,1,n)(S+=RD[i][j])%=P;//用【右下角为(i,j)的矩阵RD】求辅助线上边的总个数

    }

    return ans%P;

}

inline int L_R(){//加左-右

    Re ans=0,S=0;

    For(j,1,n){

    	For(i,1,n)(ans+=S*LU[i][j]%P)%=P;//用【左上角为(i,j)的矩阵LU】固定在辅助线右边

    	For(i,1,n)(S+=RD[i][j])%=P;//用【右下角为(i,j)的矩阵RD】求辅助线左边的总个数

    }

    return ans%P;

}

inline int LU_RD(){//减左上-右下

    Re ans=0;memset(SS,0,sizeof(SS));

    For(i,1,n-1)For(j,1,n-1){

    	SS[i][j]=((RD[i][j]+SS[i-1][j]+SS[i][j-1])%P-SS[i-1][j-1]+P)%P;

    	//十字线左上角的用【右下角为(i,j)的矩阵RD】求总和

    	(ans+=SS[i][j]*LU[i+1][j+1]%P)%=P;//用【左上角为(i,j)的矩阵LU】固定十字线的右下角

    }

    return ans;

}

inline int RU_LD(){//减右上-左下

    Re ans=0;memset(SS,0,sizeof(SS));

    For(i,1,n-1)Por(j,n,2){

    	SS[i][j]=((LD[i][j]+SS[i-1][j]+SS[i][j+1])%P-SS[i-1][j+1]+P)%P;

    	//十字线右上角的用【左下角为(i,j)的矩阵LD】求总和

    	(ans+=SS[i][j]*RU[i+1][j-1]%P)%=P;//用【右上角为(i,j)的矩阵RU】固定十字线的左下角

    }

    return ans;

}

int main(){

//  freopen("crni.in","r",stdin);

//  freopen("crni.out","w",stdout);

    in(n);

    For(i,1,n){

    	scanf("%s",ch+1);

    	For(j,1,n)A[i][j]=(ch[j]=='C');

    }

    get_RD(),get_LU(),get_LD(),get_RU();

    printf("%d\n",((U_D()+L_R())%P-(LU_RD()+RU_LD())%P+P)%P);

//  fclose(stdin);

//  fclose(stdout);

    return 0;

}