【03NOIP普及组】麦森数（信息学奥赛一本通 1925）（洛谷 1045）

【题目描述】

形如2^P-1的素数称为麦森数，这时P一定也是个素数。但反过来不一定，即如果P是个素数，2^P-1不一定也是素数。到1998年底，人们已找到了37个麦森数。最大的一个是P=3021377，它有909526位。麦森数有许多重要应用，它与完全数密切相关。

任务：输入P（1000＜P＜3100000），计算2^P-1的位数和最后500位数字(用十进制高精度数表示)

【输入】

只包含一个整数P（1000＜P＜3100000）

【输出】

第一行：十进制高精度数2^P-1的位数。

第2-11行：十进制高精度数2^P-1的最后500位数字。（每行输出50位，共输出10行，不足500位时高位补0）

不必验证2^P-1与P是否为素数。

【输入样例】

1279

【输出样例】

386

00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000 00000000000000104079321946643990819252403273640855 38615262247266704805319112350403608059673360298012 23944173232418484242161395428100779138356624832346 49081399066056773207629241295093892203457731833496 61583550472959420547689811211693677147548478866962 50138443826029173234888531116082853841658502825560 46662248318909188018470682222031405210266984354887 32958028878050869736186900714720710555703168729087

---

这道题的难点主要是在于高精+快速幂把代码搞复杂了
然而思想并不难的_(:з」∠)_

首先是求位数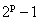：  与  有着相同的位数。

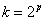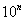因为2的次方满足了最后一位不为零的要求，所以减一后位数并不会改变，那么我们可以直接求  的位数。那么怎么求位数呢？不妨设  ，根据  的位数为 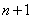 ，我们只要想办法把  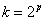中的底数2改为10，指数加一就是位数了。由此想到用10的几次方来代替2，那么就不难想到  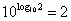，这样便可以把  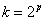中的2代换掉，变为  。根据乘方的原理，将p乘进去，原式便可化为我们最终想要的形式 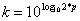 了，所以位数就是  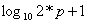。（提醒一下，C++中cmath库自带log10()函数...）

然后就是快速幂，关于快速幂可以参考下面这篇文章☟☟☟

快速幂 - endl\n - 博客园  https://www.cnblogs.com/ljy-endl/p/11307890.html

 #include<cstdio>
 #include<cmath>
 #include<cstring>
 using namespace std;
 int f[],p,res[],sav[];//乘法要开两倍长度
 void result_1()
 {
     memset(sav,,sizeof(sav));
     for(register int i=;i<=;i+=)
         for(register int j=;j<=;j+=)
             sav[i+j-]+=res[i]*f[j];//先计算每一位上的值（不进位）
     for(register int i=;i<=;i+=)
     {
         sav[i+]+=sav[i]/;//单独处理进位问题，不容易出错
         sav[i]%=;
     }
     memcpy(res,sav,sizeof(res));//cstring库里的赋值函数，把sav的值赋给res
 }
 void result_2()//只是在result_1的基础上进行了细微的修改
 {
     memset(sav,,sizeof(sav));
     for(register int i=;i<=;i+=)
         for(register int j=;j<=;j+=)
             sav[i+j-]+=f[i]*f[j];
     for(register int i=;i<=;i+=)
     {
         sav[i+]+=sav[i]/;
         sav[i]%=;
     }
     memcpy(f,sav,sizeof(f));
 }
 int main()
 {
     scanf("%d",&p);
     printf("%d\n",(int)(log10()*p+));
     res[]=;
     f[]=;//高精度赋初值
     while(p!=)//快速幂模板
     {
         if(p%==)result_1();
         p/=;
         result_2();
     }
     res[]-=;
     for(register int i=;i>=;i-=)//注意输出格式，50个换一行，第一个不用
         if(i!=&&i%==)printf("\n%d",res[i]);
         else printf("%d",res[i]);
     return ;
 }

//代码来自：题解 P1045 【麦森数】 - ForwardFuture's blog - 洛谷博客  https://www.luogu.org/blog/28916/solution-p1045