hdu1693 Eat the Trees 【插头dp】

题目链接

hdu1693

题解

插头\(dp\)

特点：范围小，网格图，连通性

轮廓线：已决策点和未决策点的分界线

插头：存在于网格之间，表示着网格建的信息，此题中表示两个网格间是否连边

状态表示：当前点\((i,j)\)和轮廓线上\(m + 1\)个插头的状态

状态转移：



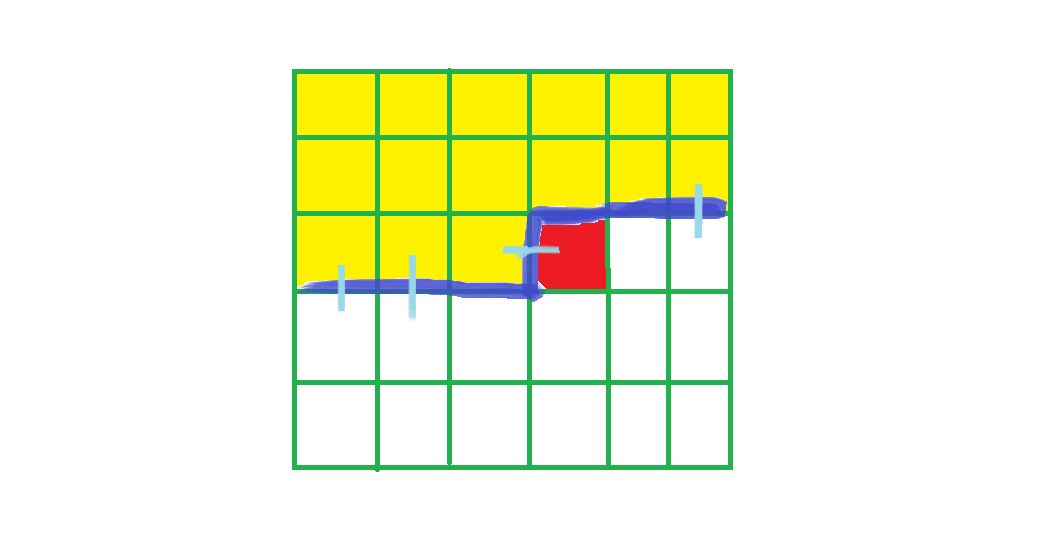
我们用\(f[i][j][s]\)表示如上的状态，最后一次决策点为\((i,j)\)，轮廓线上插头状态为\(s\)的方案数

比如上图\(s = 1101001\)

之后我们扩展新的点，枚举它插头的状态进行转移



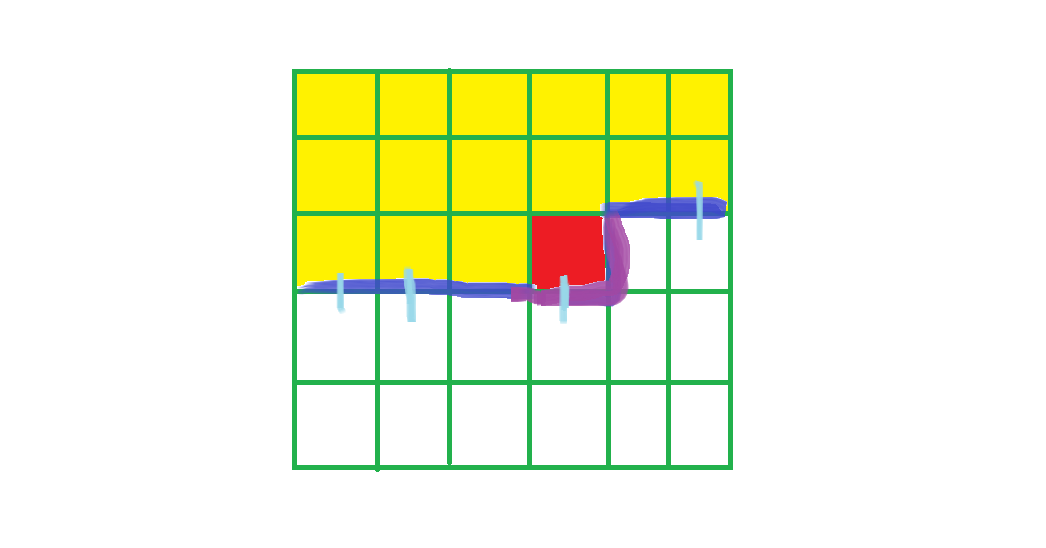
在本题中，要使最终形成若干回路，每个点度数必须为\(2\)，所以我们扩展点的时候记录它已有的插头数，然后剩余的插头数就可以唯一确定

然后就可以\(O(nm2^m)\)过了这道插头\(dp\)入门题

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<map>
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define mp(a,b) make_pair<int,int>(a,b)
#define cls(s) memset(s,0,sizeof(s))
#define cp pair<int,int>
#define LL long long int
using namespace std;
const int maxn = 12,maxm = 100005,INF = 1000000000;
inline int read(){
	int out = 0,flag = 1; char c = getchar();
	while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}
	while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
	return out * flag;
}
int n,m,S[maxn][maxn];
LL f[maxn][maxn][1 << maxn];
void work(int C){
	cls(f);
	if (!S[1][1]) f[1][1][0] = 1;
	else {
		if (S[1][2] == 0 || S[2][1] == 0){
			printf("Case %d: There are 0 ways to eat the trees.\n",C);
			return;
		}
		f[1][1][3] = 1;
	}
	int maxv = (1 << m + 1) - 1,cnt,e,t;
	for (int i = 1; i <= n; i++){
		for (int j = 1; j <= m; j++){
			if (i == n && j == m) break;
			for (int s = 0; s <= maxv; s++){
				if (!f[i][j][s]) continue;
				if (j == m){
					if (s & 1){
						if (i + 2 <= n && S[i + 2][1])
							f[i + 1][1][(s >> 1) << 2 | 1] += f[i][j][s];
						if (S[i + 1][2])
							f[i + 1][1][(s >> 1) << 2 | 2] += f[i][j][s];
					}
					else {
						if (!S[i + 1][1]) f[i + 1][1][(s >> 1) << 2] += f[i][j][s];
						else {
							if (i + 2 > n || !S[i + 2][1] || !S[i + 1][2]) continue;
							f[i + 1][1][(s >> 1) << 2 | 3] += f[i][j][s];
						}
					}
				}
				else {
					cnt = ((s >> j) & 1) + ((s >> j + 1) & 1);
					t = (s >> j) & 3; e = s ^ (t << j);
					if (cnt && !S[i][j + 1]) continue;
					if (cnt == 2) f[i][j + 1][e] += f[i][j][s];
					else if (cnt == 1){
						if (i + 1 <= n && S[i + 1][j + 1])
							f[i][j + 1][e | (1 << j)] += f[i][j][s];
						if (j + 2 <= m && S[i][j + 2])
							f[i][j + 1][e | (1 << j + 1)] += f[i][j][s];
					}
					else {
						if (!S[i][j + 1]) f[i][j + 1][e] += f[i][j][s];
						else {
							if (i + 1 > n || j + 2 > m || !S[i + 1][j + 1] || !S[i][j + 2])
								continue;
							f[i][j + 1][e | (3 << j)] += f[i][j][s];
						}
					}
				}
			}
		}
	}
	LL ans = 0;
	for (int s = 0; s <= maxv; s++)
		ans += f[n][m][s];
	printf("Case %d: There are %lld ways to eat the trees.\n",C,ans);
}
int main(){
	int T = read();
	REP(t,T){
		n = read(); m = read();
		REP(i,n) REP(j,m) S[i][j] = read();
		if (n == 1 || m == 1){
			if (!S[n][m]) printf("Case %d: There are 1 ways to eat the trees.\n",t);
			else printf("Case %d: There are 0 ways to eat the trees.\n",t);
			continue;
		}
		work(t);
	}
	return 0;
}