ural 1748 The Most Complex Number 和 丑数

题目：http://acm.timus.ru/problem.aspx?space=1&num=1748

题意：求n范围内约数个数最多的那个数。

Roughly speaking, for a number to be highly composite it has to have prime factors as small as possible, but not too many of the same. If we decompose a number n in prime factors like this:

where 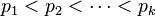are prime, and the exponents are positive integers, then the number of divisors of n is exactly

Hence, for n to be a highly composite number,

• the k given prime numbers p_i must be precisely the first k prime numbers (2, 3, 5, ...); if not, we could replace one of the given primes by a smaller prime, and thus obtain a smaller number than n with the same number of divisors (for instance 10 = 2 × 5 may be replaced with 6 = 2 × 3; both have four divisors);

• the sequence of exponents must be non-increasing, that is 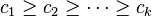; otherwise, by exchanging two exponents we would again get a smaller number than n with the same number of divisors (for instance 18 = 2¹ × 3² may be replaced with 12 = 2² × 3¹; both have six divisors).

c++ 代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

#define  ll long long
ll n, ansa, ansb;
int p[] = {, , , , , , , , , , , , , , };

void dfs(int pos, ll num, int div, int limit )
{
    if ( div>ansb || (div==ansb && num<ansa) ){
        ansa = num; ansb = div;
    }
    if (pos == ) return ;

    for ( int i=; i<=limit; ++i )
    {
        if ( n/num < p[pos]) break;
        num *= p[pos];
        dfs(pos+, num, div*(i+), i);
    }
}

int main(int argc, char**argv)
{
    int T; scanf("%d", &T);
    while ( T-- ){
        //scanf("%lld", &n);
        cin >> n;
        if (n==) {
            puts("1 1"); continue;
        }
        ansa = ansb = -;
        dfs(, , , );
        //printf("%lld %lld\n", ansa, ansb);
     cout << ansa << ' ' << ansb << endl;
    }
    return EXIT_SUCCESS;
}
                                                                                          

python 代码  注意这代码会TLE，具体是什嘛原因，我没有具体查了。貌似测试10^18都很快的。

p= [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]
ansa=0; ansb=0

def dfs(pos, num, div, limit, n):
    global ansa, ansb
    if div>ansb or ( div==ansb and ansa>num ):
        ansa = num; ansb = div
    if pos == 15: return

    for i in xrange(1, limit+1):
        if (n/num) < p[pos] : return
        num *= p[pos]
        dfs(pos+1, num, div*(i+1), i, n)

if __name__ == '__main__':
    T = input()
    while T:
        T -= 1
        n = input()
        if n == 1:
            print 1, 1; continue
        ansa = ansb = -1
        dfs(0, 1, 1, 60, n)
        print ansa, ansb

这种数有点类似与丑数，对于丑数的求法。

丑数：因子只含2，3，5的数。 例如求第n个丑数。

bruteforce 是有用的。效率太低了。

如果有一个丑数数组，那么这个数组接下来一个丑数会是哪个数呢？毫无疑问这个数是有数组里的元素乘上2，3，5里的某一个数，这个数满足大于当前丑数数组最后一个元素，最小的满足这个条件的数就是下一个丑数。即求min( 2*a， 3*b， 5*c ) ,枚举求2a，3b5c是可行的。但二分会是很不错的选择， 复杂度为o(n*3logn)。

def find(p, x):
    l = 0; r = len(p)-1
    while l<=r:
        mid = (l+r)>>1
        if x*p[mid]>p[-1]:
            r = mid-1
        else : l = mid+1
    return x*p[l]

def solve(n):
    p=[1]; cnt = 0 # cnt
    while cnt < n:
        cnt += 1
        a = find(p, 2)
        b = find(p, 3)
        c = find(p, 5)
        p.append(min(a, b, c) )
    print p[-1]

if __name__ == '__main__':
    n = input()
    solve(n)