LeetCode(3) || Median of Two Sorted Arrays

LeetCode(3) || Median of Two Sorted Arrays

题记

之前做了3题，感觉难度一般，没想到突然来了这道比较难的，星期六花了一天的时间才做完，可见以前基础太差了。

题目内容

There are two sorted arrays A and B of size m and n respectively. Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

解题思路

• 题目大致意思，有两个已经有序的数组A和B，他们的长度分别是m和n，现在要求获取两个数组的中位数且计算复杂度在O(log(m+n)).
• 题目意思比较简单，咋一想很好做么，但是考虑到时间复杂度O(log(m+n))的限制就略微有点困难了。
• 此题的难点主要在两个，一是计算复杂度，二是需要考虑很多边界情况，我在解题中就差点被淹没在无穷的边界情况中。
• 解此题我分别使用了三种方法，分别对应三种计算复杂度，O(nlog(n)),O(n),以及O(n)
  • 第一种方法O(nlog(n))是最简单，大多数人使用的，即将数组A和数组B合并成数组C，对C进行排序再求中位数。按理说这样复杂度应该不符合题目的要求的，但是我抱着不死心的态度去LeetCode尝试了下，没想到就通过了。由此可见，LeetCode的运算时间并没有想象中的那么严格。
  • 第二种方法O(n+m)需要进行一次遍历，在遍历的过程中，比较A[k]和B[i]，以从小到大顺序为例，如果A[k]<B[i]则K++，否则i++。一直到k+i达到中位数的要求。此算法的难度在于需要考虑多种边界条件。
  • 第三种方法O(log(m+n))，其实看到这个复杂度第一个反应就是对半查找，尝试了好久并未成功，后来才觉悟其实应该K值查找方法。算法内容大致如下：
    • 判断中位数的类型，即m+n若为奇数，则查找第(m+n)/2个数，否则查找第(m+n)/2和第(m+n)/2+1个数。需要考虑数组为空的情况。
    • 此时开始K值查找：

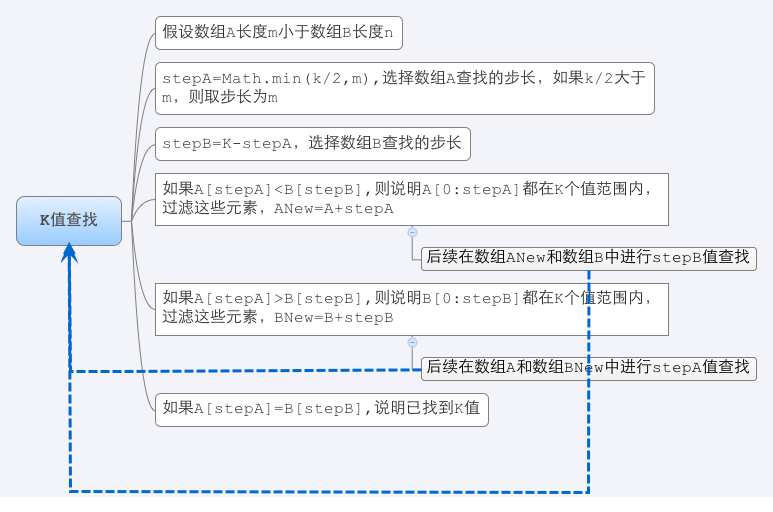
• • • K值查到其实就是查找第K个值的过程分解为查找第Min(K/2,m)和K-Min(K/2,m)两步，然后再递归进行下去。所以计算复杂度在O(log(m+n)).
    • 另外需要注意的是还需要考虑几种边界条件：
      • K=1时候，返回Min(A[0],B[0])
      • m=0时候，返回B[k-1]
      • m>n时候，需要互换数组A和数组B的位置。

解题方法

方法1：计算复杂度O(n*log(n))

 public class Solution {
     public double findMedianSortedArrays(int A[], int B[]) {
         int m = A.length;
         int n = B.length;
         int[] C = new int[m+n];
         double median = 0;
         System.arraycopy(A, 0, C, 0, A.length);
         System.arraycopy(B, 0, C, A.length, B.length);
         Arrays.sort(C);

         if ( (m + n) % 2 == 0 ) {
             median = (double)(C[(m+n)/2]+C[(m+n)/2-1])/2.0;
         }else{
             median = C[(m+n-1)/2];
         }

         return median;
     }
 }

方法2：计算复杂度O(n)

 public class Solution {
     public double findMedianSortedArrays(int A[], int B[]) {
         int m = A.length;
         int n = B.length;
         int medianIndex1 = (m + n) % 2 == 0 ? (m+n)/2-1 :(m+n-1)/2;
         int medianIndex2 = (m + n) % 2 == 0 ? (m+n)/2   :(m+n-1)/2;
         int travelA = 0;
         int travelB = 0;
         double median = 0;
         double median1 = 0;
         double median2 = 0;
         if ( m == 0 ){
             return n % 2 == 0 ? (double)(B[n/2]+B[n/2-1])/2:B[(n-1)/2];
         }

         if( n == 0 ){
             return m % 2 == 0 ? (double) (A[m/2]+A[m/2-1])/2:A[(m-1)/2];
         }

         for(int i = 0; i <= medianIndex2;i++){
             boolean flagA = true;
             if ( travelA < m && travelB < n){
                 if(A[travelA] >= B[travelB]){
                     flagA = false;
                 }else{
                     flagA = true;
                 }
             }else if ( travelA >= m){
                 flagA = false;
             }else{
                 flagA = true;
             }

             if (flagA){
                 if ( i == medianIndex1 ){
                     median1 = A[travelA];
                 }

                 if ( i == medianIndex2 ){
                     median2 = A[travelA];
                 }
                 travelA++;
             }else{
                 if ( i == medianIndex1 ){
                     median1 = B[travelB];
                 }

                 if ( i == medianIndex2 ){
                     median2 = B[travelB];
                 }
                 travelB++;
             }
         }

         if ( (m + n) % 2 == 0){
             median = (double) (median1 + median2)/2;
         }else{
             median = median1;
         }

         return median;
     }
 }

方法3：计算复杂度O(log(m+n))

    /**
      * int A[] B[] ，数组A和数组B.
      * int startA startB,子数组指针，子数组起始位置.
      * int K, 需要查找的第K个值
      * */
     public double findKthNum(int A[],int startA,int B[],int startB, int k){
         //获取数组A和数组B的子数组的数组长度
         int m = A.length - startA;
         int n = B.length - startB;
         //假设数组A短于数组B，否则数组A和数组B互换位置。
         if ( m > n){
             return findKthNum(B,startB,A,startA,k);
         }
         //数组A为空，第K个值从数组B的子串中获取
         if ( m == 0 ){
             return B[startB+k-1];
         }
         //只获取第一个数组，在数组A和数组B的子数组的第一个元素选择
         if ( k == 1 ){
             return A[startA] > B[startB] ? B[startB] : A[startA];
         }
         //将K值查找，分为min(k/2,m)和K-min(k/2,m)两步，考虑K/2>m这种情况
         int newK = Math.min(k/2,m);
         int leftK = k - newK;

         if ( A[startA+newK-1] < B[startB+leftK-1] ){
             //数组A的子数组的前newK个元素都在K值范围内，过滤这new个元素继续查找第leftK个值
             return findKthNum(A,startA+newK,B,startB,leftK);
         }else if (A[startA+newK-1] > B[startB+leftK-1]){
             //数组B的子数组的前leftK个元素都在K值范围内，过滤这leftK个元素继续查找第k-leftK个值
             return findKthNum(A,startA,B,startB+leftK,k-leftK);
         }else{
             //如果相等，则说明找到中位数
             return A[startA+newK-1];
         }
     }

     public double findMedianSortedArrays(int A[], int B[]) {
         int m = A.length;
         int n = B.length;
         if ( m == 0 ){
             //数组A为空，则在数组B内直接查找中位数
             return n % 2 == 0 ? (double)(B[n/2]+B[n/2-1])/2:B[(n-1)/2];
         }

         if( n == 0 ){
             //数组B为空，则在数组A内直接查找中位数
             return m % 2 == 0 ? (double) (A[m/2]+A[m/2-1])/2:A[(m-1)/2];
         }

         if ( (m + n) %2 != 0){
             //m+n为奇数，查找第(m+n)/2+1个数
             return findKthNum(A,0,B,0,(m+n)/2+1);
         }else{
             //m+n为偶数，查找第(m+n)/2合(m+n)/2+1个数
             return ((double) (findKthNum(A,0,B,0,(m+n)/2) + findKthNum(A,0,B,0,(m+n)/2+1)))/2;
         }
     }