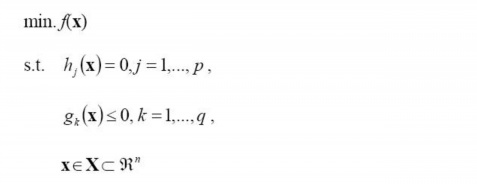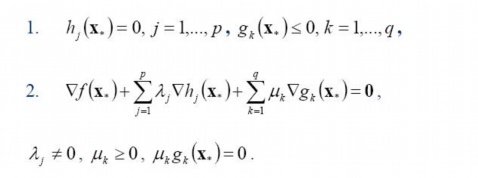支持向量机通俗导论(理解SVM的三层境地)
支持向量机通俗导论(理解SVM的三层境地)
作者:July ;致谢:pluskid、白石、JerryLead。
出处:结构之法算法之道blog。
前言
动笔写这个支持向量机(support vector machine)是费了不少劲和困难的,原因非常简单,一者这个东西本身就并不好懂,要深入学习和研究下去需花费不少时间和精力,二者这个东西也不好讲清楚,尽管网上已经有朋友写得不错了(见文末參考链接),但在描写叙述数学公式的时候还是显得不够。得益于同学白石的数学证明,我还是想尝试写一下,希望本文在兼顾通俗易懂的基础上,真真正正能足以成为一篇完整概括和介绍支持向量机的导论性的文章。
本文在写的过程中,參考了不少资料,包含《支持向量机导论》、《统计学习方法》及网友pluskid的支持向量机系列等等,于此,还是一篇或者-1,分别代表两个不同的类),一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面(hyper plane),这个超平面的方程能够表示为( wT中的T代表转置):
或-1有疑问,事实上,这个1或-1的分类标准起源于logistic回归,负例的特征远小于0,并且要在全部训练实例上达到这个目标。
接下来,尝试把logistic回归做个变形。首先,将使用的结果标签y = 0和y = 1替换为y = -1,y = 1,然后将 (
( )中的
)中的
 替换为
替换为 (即
(即 )。如此,则有了
)。如此,则有了 。也就是说除了y由y=0变为y=-1外,线性分类函数跟logistic回归的形式化表示
。也就是说除了y由y=0变为y=-1外,线性分类函数跟logistic回归的形式化表示 没差别。
没差别。
进一步,能够将假设函数 中的g(z)做一个简化,将其简单映射到y=-1和y=1上。映射关系例如以下:
中的g(z)做一个简化,将其简单映射到y=-1和y=1上。映射关系例如以下:
1.2、线性分类的一个样例
下面举个简单的样例,例如以下图所看到的,如今有一个二维平面,平面上有两种不同的数据,分别用圈和叉表示。由于这些数据是线性可分的,所以能够用一条直线将这两类数据分开,这条直线就相当于一个超平面,超平面一边的数据点所相应的y全是 -1 ,还有一边所相应的y全是1。
这个超平面能够用分类函数
注:有的资料上定义特征到结果的输出函数



 的时候,为了求解方便,会把yf(x)令为1,即yf(x)是y(w^x + b),还是y(w^x - b),对我们要优化的式子max1/||w||已无影响。
的时候,为了求解方便,会把yf(x)令为1,即yf(x)是y(w^x + b),还是y(w^x - b),对我们要优化的式子max1/||w||已无影响。
(则将x的类别赋为-1,假设f(x)大于0则将x的类别赋为1。
接下来的问题是,怎样确定这个超平面呢?从直观上而言,这个超平面应该是最适合分开两类数据的直线。而判定“最适合”的标准就是这条直线离直线两边的数据的间隔最大。所以,得寻找有着最大间隔的超平面。
1.3、函数间隔Functional margin与几何间隔Geometrical margin
倍(尽管此时超平面没有改变),所以仅仅有函数间隔还远远不够。
事实上,我们能够对法向量w加些约束条件,从而引出真正定义点到超平面的距离--几何间隔(geometrical margin)的概念。
假定对于一个点 x ,令其垂直投影到超平面上的相应点为 x0 ,w 是垂直于超平面的一个向量,
有
又由于 x0 是超平面上的点,满足 f(x0)=0 ,代入超平面的方程
γ
(有的书上会写成把||w|| 分开相除的形式,如本文參考文献及推荐阅读条目11,当中,||w||为w的二阶泛数)
为了得到


从上述函数间隔和几何间隔的定义能够看出:几何间隔就是函数间隔除以||w||,并且函数间隔y*(wx+b) = y*f(x)实际上就是|f(x)|,仅仅是人为定义的一个间隔度量,而几何间隔|f(x)|/||w||才是直观上的点到超平面的距离。
1.4、最大间隔分类器M),而对于全部不是支持向量的点,则显然有 。
。

OK,到此为止,算是了解到了SVM的第一层,对于那些仅仅关心怎么用SVM的朋友便已足够,不必再更进一层深究其更深的原理。
第二层、深入SVM
2.1、从线性可分到线性不可分
2.1.1、从原始问题到对偶问题的求解
接着考虑之前得到的目标函数:
 的最大值相当于求
的最大值相当于求 的最小值,所以上述目标函数等价于(w由分母变成分子,从而也有原来的max问题变为min问题,非常明显,两者问题等价):
的最小值,所以上述目标函数等价于(w由分母变成分子,从而也有原来的max问题变为min问题,非常明显,两者问题等价):由于如今的目标函数是二次的,约束条件是线性的,所以它是一个凸二次规划问题。这个问题能够用现成的QP (Quadratic Programming) 优化包进行求解。一言以蔽之:在一定的约束条件下,目标最优,损失最小。
此外,由于这个问题的特殊结构,还能够通过拉格朗日对偶性(Lagrange Duality)变换到对偶变量 (dual variable) 的优化问题,即通过求解与原问题等价的对偶问题(dual problem)得到原始问题的最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的长处在于:一者对偶问题往往更easy求解;二者能够自然的引入核函数,进而推广到非线性分类问题。
那什么是拉格朗日对偶性呢?简单来讲,通过给每个约束条件加上一个拉格朗日乘子(Lagrange multiplier)
然后令
easy验证,当某个约束条件不满足时,比如



因此,在要求约束条件得到满足的情况下最小化



详细写出来,目标函数变成了:
这里用

交换以后的新问题是原始问题的对偶问题,这个新问题的最优值用


换言之,之所以从minmax的原始问题



下面能够先求L 对w、b的极小,再求L 对
2.1.2、KKT条件
上文中提到“

一般地,一个最优化数学模型能够表示成下列标准形式:
当中,f(x)是须要最小化的函数,h(x)是等式约束,g(x)是不等式约束,p和q分别为等式约束和不等式约束的数量。
同一时候,得明确下面两点:
- 凸优化的概念:
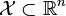 为一凸集,
为一凸集, 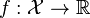 为一凸函数。凸优化就是要找出一点
为一凸函数。凸优化就是要找出一点 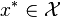 ,使得每一
,使得每一  满足
满足 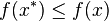 。
。 - KKT条件的意义:它是一个非线性规划(Nonlinear Programming)问题能有最优化解法的必要和充分条件。
而KKT条件就是指上面最优化数学模型的标准形式中的最小点 x* 必须满足下面的条件:
经过论证,我们这里的问题是满足 KKT 条件的(首先已经满足Slater condition,再者f和gi也都是可微的,即L对w和b都可导),因此如今我们便转化为求解第二个问题。
也就是说,原始问题通过满足KKT条件,已经转化成了对偶问题。而求解这个对偶学习问题,分为3个步骤:首先要让L(w,b,a) 关于 w 和 b 最小化,然后求对
2.1.3、对偶问题求解的3个步骤
(1)、首先固定
注意上面的形式,假设我们构造另外一个五维的空间,当中五个坐标的值分别为 Z1=X1, Z2=X21, Z3=X2, Z4=X22, Z5=X1X2,那么显然,上面的方程在新的坐标系下能够写作:
关于新的坐标 Z ,这正是一个 hyper plane 的方程!也就是说,假设我们做一个映射 ϕ:R2→R5 ,将 X 依照上面的规则映射为 Z ,那么在新的空间中原来的数据将变成线性可分的,从而使用之前我们推导的线性分类算法就能够进行处理了。这正是 Kernel 方法处理非线性问题的基本思想。
再进一步描写叙述 Kernel 的细节之前,最好还是再来看看这个样例映射过后的直观样例。当然,你我可能无法把 5 维空间画出来,只是由于我这里生成数据的时候就是用了特殊的情形,详细来说,我这里的超平面实际的方程是这个样子(圆心在 X2 轴上的一个正圆):
因此我仅仅须要把它映射到 Z1=X21, Z2=X22, Z3=X2 这样一个三维空间中就可以,下图即是映射之后的结果,将坐标轴经过适当的旋转,就能够非常明显地看出,数据是能够通过一个平面来分开的(pluskid:下面的gif 动画,先用 Matlab 画出一张张图片,再用 Imagemagick 拼贴成):
核函数相当于把原来的分类函数:
映射成:
而当中的
这样一来问题就攻克了吗?似乎是的:拿到非线性数据,就找一个映射 


 ,然后一股脑把原来的数据映射到新空间中,再做线性 SVM 就可以。只是事实上没有这么简单!事实上刚才的方法稍想一下就会发现有问题:在最初的样例里,我们对一个二维空间做映射,选择的新空间是原始空间的全部一阶和二阶的组合,得到了五个维度;假设原始空间是三维,那么我们会得到 19 维的新空间,这个数目是呈爆炸性增长的,这给
,然后一股脑把原来的数据映射到新空间中,再做线性 SVM 就可以。只是事实上没有这么简单!事实上刚才的方法稍想一下就会发现有问题:在最初的样例里,我们对一个二维空间做映射,选择的新空间是原始空间的全部一阶和二阶的组合,得到了五个维度;假设原始空间是三维,那么我们会得到 19 维的新空间,这个数目是呈爆炸性增长的,这给 


 的计算带来了非常大的困难,并且假设遇到无穷维的情况,就根本无从计算了。所以就须要 Kernel 出马了。
的计算带来了非常大的困难,并且假设遇到无穷维的情况,就根本无从计算了。所以就须要 Kernel 出马了。
最好还是还是从最開始的简单样例出发,设两个向量 和
和 ,而
,而 即是到前面说的五维空间的映射,因此映射过后的内积为:
即是到前面说的五维空间的映射,因此映射过后的内积为:
(公式说明:上面的这两个推导过程中,所说的前面的五维空间的映射,这里说的前面便是文中2.2.1节的所述的映射方式,回想下之前的映射规则,再看那第一个推导,事实上就是计算x1,x2各自的内积,然后相乘相加就可以,第二个推导则是直接平方,去掉括号,也非常easy推出来)
另外,我们又注意到:
二者有非常多类似的地方,实际上,我们仅仅要把某几个维度线性缩放一下,然后再加上一个常数维度,详细来说,上面这个式子的计算结果实际上和映射
之后的内积 的结果是相等的,那么差别在于什么地方呢?
的结果是相等的,那么差别在于什么地方呢?
- 一个是映射到高维空间中,然后再依据内积的公式进行计算;
- 而还有一个则直接在原来的低维空间中进行计算,而不须要显式地写出映射后的结果。
(公式说明:上面之中,最后的两个式子,第一个算式,是带内积的全然平方式,能够拆开,然后,通过凑一个得到,第二个算式,也是依据第一个算式凑出来的)
回想刚才提到的映射的维度爆炸,在前一种方法已经无法计算的情况下,后一种方法却依然能从容处理,甚至是无穷维度的情况也没有问题。
我们把这里的计算两个向量在隐式映射过后的空间中的内积的函数叫做核函数 (Kernel Function) ,比如,在刚才的样例中,我们的核函数为:
核函数能简化映射空间中的内积运算——刚好“碰巧”的是,在我们的 SVM 里须要计算的地方数据向量总是以内积的形式出现的。对照刚才我们上面写出来的式子,如今我们的 ,由于 w 是垂直于超平面的一个向量,

3.2、非线性学习器
3.2.1、Mercer定理
 上的映射(也就是从两个n维向量映射到实数域)。那么假设K是一个有效核函数(也称为Mercer核函数),那么当且仅当对于训练样例
上的映射(也就是从两个n维向量映射到实数域)。那么假设K是一个有效核函数(也称为Mercer核函数),那么当且仅当对于训练样例 ,其相应的核函数矩阵是对称半正定的。
,其相应的核函数矩阵是对称半正定的。 3.3、损失函数
在本文1.0节有这么一句话“支持向量机(SVM)是90年代中期发展起来的基于统计学习理论的一种机器学习方法,通过寻求结构化风险最小来提高学习机泛化能力,实现经验风险和置信范围的最小化,从而达到在统计样本量较少的情况下,亦能获得良好统计规律的目的。”但初次看到的读者可能并不了解什么是结构化风险,什么又是经验风险。要了解这两个所谓的“风险”,还得又从监督学习说起。
监督学习实际上就是一个经验风险或者结构风险函数的最优化问题。风险函数度量平均意义下模型预測的好坏,模型每一次预測的好坏用损失函数来度量。它从假设空间F中选择模型f作为决策函数,对于给定的输入X,由f(X)给出相应的输出Y,这个输出的预測值f(X)与真实值Y可能一致也可能不一致,用一个损失函数来度量预測错误的程度。损失函数记为L(Y, f(X))。
经常使用的损失函数有下面几种(基本引用自《统计学习方法》):
如此,SVM有另外一种理解,即最优化+损失最小,或如@夏粉_百度所说“可从损失函数和优化算法角度看SVM,boosting,LR等算法,可能会有不同收获”。
OK,关于很多其它统计学习方法的问题,请參看此文。
关于损失函数,例如以下文读者评论中所述:能够看看张潼的这篇《Statistical behavior and consistency of classification methods based on convex risk minimization》。各种算法中经常使用的损失函数基本都具有fisher一致性,优化这些损失函数得到的分类器能够看作是后验概率的“代理”。
此外,他还有另外一篇论文《Statistical analysis of some multi-category large margin classification methods》,在多分类情况下margin loss的分析,这两篇对Boosting和SVM使用的损失函数分析的非常透彻。
3.4、最小二乘法
3.4.1、什么是最小二乘法?
既然本节開始之前提到了最小二乘法,那么下面引用《正态分布的前世今生》里的内容略微简单阐述下。
我们口头中经常说:一般来说,平均来说。如平均来说,不吸烟的健康优于吸烟者,之所以要加“平均”二字,是由于凡事皆有例外,总存在某个特别的人他吸烟但由于经常锻炼所以他的健康状况可能会优于他身边不吸烟的朋友。而最小二乘法的一个最简单的样例便是算术平均。
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法能够简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。用函数表示为:
使误差「所谓误差,当然是观察值与实际真实值的差量」平方和达到最小以寻求预计值的方法,就叫做最小二乘法,用最小二乘法得到的预计,叫做最小二乘预计。当然,取平方和作为目标函数仅仅是众多可取的方法之中的一个。
最小二乘法的一般形式可表示为:
有效的最小二乘法是勒让德在 1805 年发表的,基本思想就是觉得測量中有误差,所以全部方程的累积误差为
我们求解出导致累积误差最小的參数就可以:
勒让德在论文中对最小二乘法的优良性做了几点说明:
- 最小二乘使得误差平方和最小,并在各个方程的误差之间建立了一种平衡,从而防止某一个极端误差取得支配地位
- 计算中仅仅要求偏导后求解线性方程组,计算过程明确便捷
- 最小二乘能够导出算术平均值作为预计值
对于最后一点,从统计学的角度来看是非常重要的一个性质。推理例如以下:假设真值为 θ, x1,⋯,xn为n次測量值, 每次測量的误差为ei=xi−θ,按最小二乘法,误差累积为
求解


由于算术平均是一个历经考验的方法,而以上的推理说明,算术平均是最小二乘的一个特例,所以从还有一个角度说明了最小二乘方法的优良性,使我们对最小二乘法更加有信心。
最小二乘法发表之后非常快得到了大家的认可接受,并迅速的在数据分析实践中被广泛使用。只是历史上又有人把最小二乘法的发明归功于高斯,这又是怎么一回事呢。高斯在1809年也发表了最小二乘法,并且声称自己已经使用这种方法多年。高斯发明了小行星定位的数学方法,并在数据分析中使用最小二乘方法进行计算,准确的预測了谷神星的位置。
说了这么多,貌似跟本文的主题SVM没啥关系呀,别急,请让我继续阐述。本质上说,最小二乘法即是一种參数预计方法,说到參数预计,咱们得从一元线性模型说起。
3.4.2、最小二乘法的解法
- 监督学习中,假设预測的变量是离散的,我们称其为分类(如决策树,支持向量机等),假设预測的变量是连续的,我们称其为回归。
- 回归分析中,假设仅仅包含一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这样的回归分析称为一元线性回归分析。
- 假设回归分析中包含两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
- 对于二维空间线性是一条直线;对于三维空间线性是一个平面,对于多维空间线性是一个超平面...
- 用“残差和最小”确定直线位置是一个途径。但非常快发现计算“残差和”存在相互抵消的问题。
- 用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比較麻烦。
- 最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比較方便外,得到的预计量还具有优良特性。这样的方法对异常值非常敏感。
最经常使用的是普通最小二乘法( Ordinary Least Square,OLS):所选择的回归模型应该使全部观察值的残差平方和达到最小,即採用平方损失函数。
 ,以
,以 为变量,把它们看作是Q的函数,就变成了一个求极值的问题,能够通过求导数得到。
为变量,把它们看作是Q的函数,就变成了一个求极值的问题,能够通过求导数得到。OK,很多其它请參看陈希孺院士的《数理统计学简史》的第4章、最小二乘法,和本文參考条目第59条《凸函数》。
3.5、SMO算法
在上文中,我们提到了求解对偶问题的序列最小最优化SMO算法,日,用chrome浏览器打开文章,右键打印,弹出打印框,把左上角的目标更改为“另存为PDF”,成第一个PDF:http://vdisk.weibo.com/s/zrFL6OXKghu5V。
本文会一直不断翻新,再者,上述3个PDF的阅读体验也还不是最好的,假设有朋友制作了更好的PDF,欢迎分享给我:http://weibo.com/julyweibo,谢谢。
July、二零一四年二月十一日于天通苑。
支持向量机通俗导论(理解SVM的三层境地)的更多相关文章
- 支持向量机通俗导论 ——理解SVM的三层境界 总结
1.什么是支持向量机(SVM) 所谓支持向量机,顾名思义,分为两部分了解:一,什么是支持向量(简单来说,就是支持或支撑平面上把两类类别划分开来的超平面的向量点):二,这里的“机(machine,机器) ...
- 支持向量机通俗导论(SVM学习)
1.了解SVM 支持向量机,因其英文名为support vector machine,故一般简称SVM,通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是 ...
- 支持向量机通俗导论(理解SVM的三层境界)(ZT)
支持向量机通俗导论(理解SVM的三层境界) 原文:http://blog.csdn.net/v_JULY_v/article/details/7624837 作者:July .致谢:pluskid.白 ...
- 支持向量机通俗导论(理解SVM的三层境界)【非原创】
支持向量机通俗导论(理解SVM的三层境界) 作者:July :致谢:pluskid.白石.JerryLead. 出处:结构之法算法之道blog. 前言 动笔写这个支持向量机(support vecto ...
- 支持向量机通俗导论(理解SVM的三层境界) by v_JULY_v
支持向量机通俗导论(理解SVM的三层境界) 前言 动笔写这个支持向量机(support vector machine)是费了不少劲和困难的,原因很简单,一者这个东西本身就并不好懂,要深入学习和研究下去 ...
- 支持向量机通俗导论(理解SVM的三层境界)
原文链接:http://blog.csdn.net/v_july_v/article/details/7624837 作者:July.pluskid :致谢:白石.JerryLead 出处:结构之法算 ...
- 支持向量机通俗导论(理解SVM的三层境界)[转]
作者:July .致谢:pluskid.白石.JerryLead.说明:本文最初写于2012年6月,而后不断反反复复修改&优化,修改次数达上百次,最后修改于2016年11月.声明:本文于201 ...
- 简介支持向量机热门(认识SVM三位置)
支持向量机通俗导论(理解SVM的三层境地) 作者:July .致谢:pluskid.白石.JerryLead.出处:结构之法算法之道blog. 前言 动笔写这个支持向量机(support vector ...
- 机器学习之深入理解SVM
在浏览本篇博客之前,最好先查看一下我写的还有一篇文章机器学习之初识SVM(点击可查阅哦).这样能够更好地为了结以下内容做铺垫! 支持向量机学习方法包括构建由简至繁的模型:线性可分支持向量机.线性支持向 ...
随机推荐
- OC - 10.使用Quartz2D绘制个性头像
效果图 将一张图片剪切成圆形 在图片周围显示指定宽度和颜色的边框 实现思路 效果图中主要由不同尺寸的两大部分组成 蓝色的背景区域,尺寸等于图片的尺寸加上边框的尺寸 图片区域,尺寸等于图片的尺寸 绘 ...
- 使用GitBook编写文档
GitBook 简介 GitBook 是一个通过 Git 和 Markdown 来撰写书籍的工具,最终可以生成 3 种格式: 静态站点:包含了交互功能(例如搜索.书签)的站点 PDF:PDF 格式的文 ...
- html form <label>标签基础语法结构与使用案例教程(转载)
在表单布局中会遇到label标签的使用,label没有任何样式效果,有触发对应表单控件功能.比如我们点击单选按钮或多选框前文字对应选项就能被选中,这个就是对文字加了<label>标签实现. ...
- PHP错误报告级别及调整方法
运行PHP脚本时,PHP解析器会尽其所能能报告它遇到的问题.在PHP中错误报告的处理行为,都是通过PHP的配置文件php.ini中有关的配置指令确定的.另外PHP的错误报告有很多种级别,可以根据不同的 ...
- JQuery学习笔记【CSS选择符】--02
Jquery的程序入口: <html> <head> <title></title> <script type="text/javasc ...
- ppt怎么换背景图片|PPT换背景设置方法
PPT怎么换背景?PPT背景可谓是PPT幻灯片的灵魂,优美绚丽的PPT背景能为自己做的PPT幻灯片锦上添花.今天,格子啦小编就教大家PPT换背景的方法,让你不再羡慕别人所做PPT的美丽背景,也可以自己 ...
- 10:Hello, World!的大小
总时间限制: 1000ms 内存限制: 65536kB 描述 还记得在上一章里,我们曾经输出过的“Hello, World!”吗? 它虽然不是本章所涉及的基本数据类型的数据,但我们同样可以用siz ...
- [转载]在 Windows 10 中, 如何卸载和重新安装 OneNote App
在 Windows 10 中, 如何卸载和重新安装 OneNote App 15/8/2015 使用 PowerShell 命令卸载 OneNote App 开始菜单 -> 输入 "P ...
- SQL中 WHERE与HAVING的区别
SQL语句中的Having子句与where子句之区别 在说区别之前,得先介绍GROUP BY这个子句,而在说GROUP子句前,又得先说说“聚合函数”——SQL语言中一种特殊的函数.例如SUM, COU ...
- POJ2242 The Circumference of the Circle(几何)
题目链接. 题目大意: 给定三个点,即一个任意三角形,求外接圆的周长. 分析: 外接圆的半径可以通过公式求得(2*r = a/sinA = b/sinB = c/sinC),然后直接求周长. 注意: ...