sonar扫描java、js、jsp技术

最近在弄sonar扫描的事情，之前一直只能扫描java代码，这样统计出来的数据上报领导很多开发人员不服(说我不用写jsp了不用写js了？)，

那么好，于是乎继续整sonar，在官网中看到sonar其实有js、jsp的插件，这样一来，就可以实现扫描js和jsp了。

安装sonar服务器这里就不细说

要扫描js、jsp那肯定得给sonar服务器加插件，加插件可在sonar更新中心加，也可以下载jar包放到sonar的plugins下

1)JavaScript代码检查：http://docs.codehaus.org/display/SONAR/JavaScript+Plugin

2)Web页面检查（HTML、JSP、JSF、Ruby、PHP等）：http://docs.codehaus.org/display/SONAR/Web+Plugin

一、maven项目扫描java、js、jsp

sonar提供对maven的集成，所以maven项目扫描是非常简便（sonar集成maven这里不细说，网上一大票文章）

那么sonar怎么扫描三种语言的信息呢，很简单，配置pom.xml，把sonar扫描的资源路径配成java、jsp、js的资源的根路径就完了

<properties>
    <project.build.sourceEncoding>UTF-8</project.build.sourceEncoding>
    <sonar.sources>src</sonar.sources>
</properties>

扫描后sonar里显示情况：

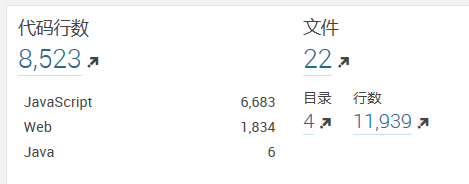
二、一般web项目扫描

一般项目推荐使用sonar-runner，sonar-runner和sonar集成达成扫描效果，

这里需要配置sonar-project.properties，然后使用sonar-runner去扫描

#required metadata
#projectKey项目的唯一标识，不能重复
sonar.forceAuthentication=false
sonar.login=saq
sonar.password=000000
sonar.projectKey=testuser
sonar.projectName=testuser
sonar.projectVersion=1.0
sonar.sourceEncoding=UTF-8
sonar.modules=java-module,javascript-module,html-module  

# Java module
java-module.sonar.projectName=Java Module
java-module.sonar.language=java
# .表示projectBaseDir指定的目录
java-module.sonar.sources=.
java-module.sonar.projectBaseDir=src/main/java
sonar.binaries=classes

# JavaScript module
javascript-module.sonar.projectName=JavaScript Module
javascript-module.sonar.language=js
javascript-module.sonar.sources=js
javascript-module.sonar.projectBaseDir=src/main/webapp 

# Html module
html-module.sonar.projectName=Html Module
html-module.sonar.language=web
html-module.sonar.sources=pages
html-module.sonar.projectBaseDir=src/main/webapp