[题解]AtCoder Beginner Contest 413(ABC413) A~G

A - Content Too Large

输出Yes\(\iff \sum a_i\le m\)。

时间复杂度\(O(n)\)。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n,m;
signed main(){
	cin>>n>>m;
	for(int i=1,x;i<=n;i++) cin>>x,m-=x;
	cout<<(m<0?"No\n":"Yes\n");
	return 0;
}

B - cat 2

枚举\(i,j\)，扔到set里面统计即可。

时间复杂度\(O(n^2\log(n^2))=O(n^2\log n)\)。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=105;
int n;
string s[N];
set<string> se;
signed main(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>s[i];
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(i!=j) se.insert(s[i]+s[j]);
		}
	}
	cout<<se.size();
	return 0;
}

C - Large Queue

操作\(1\)，将输入的\((c,x)\)作为一个整体，压入队列。

操作\(2\)，不断出队列，直到\(k\)为\(0\)为止。若最后一个出队列的元素还没用完，再把剩下的从队头压入回队列。

因为出入栈次数上界都是\(2q\)，所以时间复杂度为\(O(q)\)。

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int Q=2e5+10;
int n;
deque<pair<int,int>> q;
signed main(){
	cin>>n;
	int op,c,x;
	while(n--){
		cin>>op;
		if(op==1){
			cin>>c>>x;
			q.push_back({c,x});
		}else{
			int ans=0;
			cin>>c;
			while(!q.empty()){
				auto t=q.front();
				q.pop_front();
				if(c<t.first){
					ans+=c*t.second;
					q.push_front({t.first-c,t.second});
					break;
				}
				c-=t.first;
				ans+=t.first*t.second;
			}
			cout<<ans<<"\n";
		}
	}
	return 0;
}

D - Make Geometric Sequence

下文中\(r\)表示公比。

对于\(|r|<1\)，我们可以通过将序列翻转来让\(|r|\ge 1\)。

因此仅需判断是否存在这样的\(|r|\ge 1\)即可。

所以我们仅需将\(a\)按绝对值从小到大排序，看相邻元素是否都满足：

\[\frac{a_{i-1}}{a_i}=\frac{a_i}{a_{i+1}}
\]

即：

\[a_{i-1}\times a_{i+1}=a_i^2
\]

然而我们发现\(r=-1\)的情况下，排序得到的\(a\)会有不同的形态。此时需要特判一下，即：

• 若将满足\(a[i]=a[1]\)的\(i\)的个数记为\(x\)，\(a[i]=-a[i]\)的\(i\)的个数记为\(y\)，则有\(x+y=n\)且\(|x-y|\le 1\)。

时间复杂度\(O(n\log n)\)。

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+10;
int t,n,a[N];
bool solve(){
	cin>>n;
	int c1=0,c2=0;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<=n;i++)
		if(a[i]==a[1]) c1++;
		else if(a[i]==-a[1]) c2++;
	if(c1+c2==n&&abs(c1-c2)<2) return 1;
	sort(a+1,a+1+n,[](int a,int b){return abs(a)<abs(b);});
	for(int i=2;i<n;i++)
		if(a[i]*a[i]!=a[i-1]*a[i+1]) return 0;
	return 1;
}
signed main(){
	cin>>t;
	while(t--) cout<<(solve()?"Yes\n":"No\n");
	return 0;
}

E - Reverse 2^i

转化一下题意，相当于一棵完全二叉树，叶子节点存储的是\(a_1,a_2,\dots,a_{2^n}\)。可以任意次交换某个节点的左右子树。最后要使得叶子结点的字典序最小。

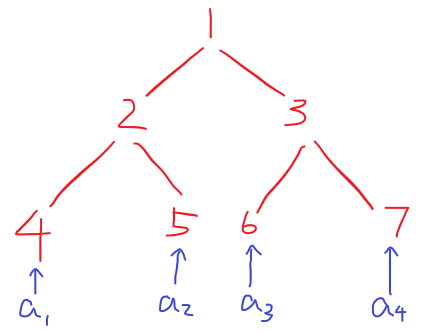
那么就有一个显然的贪心思路：每个节点仅需让左右子树中，\(\min\)值较小的那个作为左子树。

因为满足最优子结构所以正确性可以保证。

时间复杂度\(O(2^n)\)。

点击查看代码

#include<bits/stdc++.h>
const int N=(1<<18)+10;
using namespace std;
int t,n,nn,f[N<<1],l[N],r[N];
void dfs(int x){
	if(x<nn) dfs(l[x]),dfs(r[x]);
	else cout<<f[x]<<" ";
}
signed main(){
	cin>>t;
	while(t--){
		cin>>n;
		nn=(1<<n);
		for(int i=0;i<nn;i++) cin>>f[nn+i];
		for(int i=nn-1;~i;i--){
			f[i]=min(f[l[i]=(i<<1)],f[r[i]=(i<<1|1)]);
			if(f[l[i]]>f[r[i]]) swap(l[i],r[i]);
		}
		dfs(1);
		cout<<"\n";
	}
	return 0;
}

F - No Passage

若没有Aoki的限制，我们使用BFS跑一遍最短路就可以。

加上限制之后，我们定义\(d[i][j]\)表示从\((i,j)\)开始，在Aoki的限制之下到达目标格子的最少步数。

Aoki为了让\((i,j)\)步数最大，一定会把周围\(d\)值最小的方向禁用掉。

因此\(d[i][j]\)仅能从周围次小的\(d\)值进行转移。

时间复杂度\(O(nm)\)。

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e3+10,M=3e3+10;
int n,m,k,d[N][M],dx[4]{-1,0,1,0},dy[4]{0,1,0,-1},ans;
queue<pair<int,int>> q;
int sec(int x,int y){
	vector<int> v={d[x][y-1],d[x][y+1],d[x-1][y],d[x+1][y]};
	sort(v.begin(),v.end());
	return v[1];
}
signed main(){
	memset(d,0x3f,sizeof d);
	cin>>n>>m>>k;
	for(int i=1,x,y;i<=k;i++){
		cin>>x>>y;
		d[x][y]=0;
		q.push({x,y});
	}
	while(!q.empty()){
		auto t=q.front();
		q.pop();
		int x=t.first,y=t.second;
		for(int i=0;i<4;i++){
			int xx=x+dx[i],yy=y+dy[i];
			if(xx<1||xx>n||yy<1||yy>m) continue;
			int td=sec(xx,yy);
			if(td+1<d[xx][yy]){
				d[xx][yy]=td+1;
				q.push({xx,yy});
			}
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(d[i][j]!=d[0][0]){
				ans+=d[i][j];
			}
		}
	}
	cout<<ans<<"\n";
	return 0;
}

G - Big Banned Grid

\((1,1)\)走不到\((n,m)\)，当且仅当存在一个障碍物组成的八连通分量，使得它同时连接左/下边缘和右/上边缘。

八连通即通过八个方向可以走到。

时间复杂度\(O(k\log k)\)。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n,m,k;
vector<int> lef,bot;
set<pair<int,int>> se;
int dx[8]{-1,-1,0,1,1,1,0,-1},dy[8]{0,1,1,1,0,-1,-1,-1};
bool dfs(int x,int y){
	if(se.find({x,y})==se.end()) return 0;
	se.erase({x,y});
	if(x==1||y==m) return 1;
	for(int i=0;i<8;i++){
		int xx=x+dx[i],yy=y+dy[i];
		if(xx<1||xx>n||yy<1||yy>m) continue;
		if(dfs(xx,yy)) return 1;
	}
	return 0;
}
signed main(){
	cin>>n>>m>>k;
	for(int i=1,x,y;i<=k;i++){
		cin>>x>>y;
		se.insert({x,y});
		if(x==n) bot.push_back(y);
		if(y==1) lef.push_back(x);
	}
	for(int i:bot) if(dfs(n,i)) cout<<"No\n",exit(0);
	for(int i:lef) if(dfs(i,1)) cout<<"No\n",exit(0);
	cout<<"Yes\n";
	return 0;
}

---

F、G参考：https://www.cnblogs.com/stelayuri/p/18968065