Games 103 cloth PDB 浅析

简介

PDB 比 隐式积分法 速度快很多.

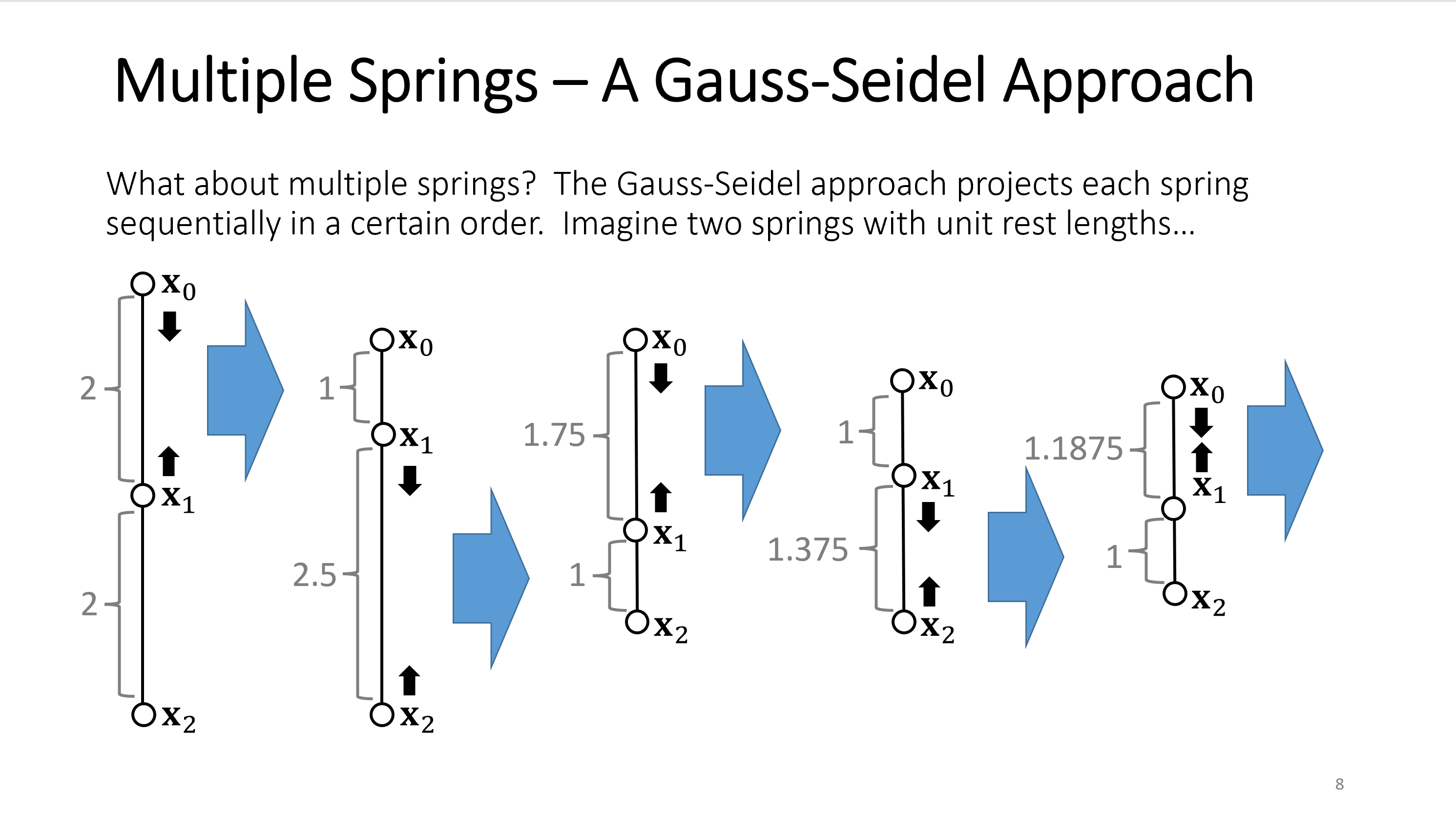
全称 Position Based Dynamics 粒子动力学系统, 什么是PBD呢? 个人的理解就是, 多次迭代, 达到一步的稳定状态. 然后更新整个系统的状态. 简单的说, 就是对于局部的模拟扩展到全局. 经过一定的迭代, 达到稳态.

可以参看Image中的第一幅图片. 对于单个系统的更新, 导致的全局的收敛. 但是必须达到多次迭代, 才能达到类似整体的一次迭代.

参考文献

师弟代码~~

Q&A

Q1

In the Update function, set up the PBD solver as a particle system. Specifically, for every vertex, damp the velocity (as in 1.a), update the velocity by gravity, and finally

update the position:

\[\mathbf{x}_{i} \leftarrow \mathbf{x}_{i}+\Delta t \mathbf{v}_{i}
\]

简单而言就是, 改变速度. 通过重力改变, 然后加上速度衰减, 然后根据速度的改变更新坐标.

			V[i] += g * t;
			V[i] *= damping;
			X[i] += t * V[i];

Q2

1.b. Strain limiting (4 Points) In the Strain Limiting function, implement position-based

dynamics in a Jacobi fashion. The basic idea is to define two temporary arrays sum x[] and sum n[]

to store the sums of vertex position updates and vertex count updates. At the beginning of the

function, set both arrays to zeros. After that, for every edge e connecting i and j, update the arrays:

\[\begin{array}{ll}
\operatorname{sum}_{\mathbf{}} \mathbf{x}_{i} \leftarrow \operatorname{sum}_{-} \mathbf{x}_{i}+\frac{1}{2}\left(\mathbf{x}_{i}+\mathbf{x}_{j}+L_{e} \frac{\mathbf{x}_{i}-\mathbf{x}_{j}}{\left\|\mathbf{x}_{i}-\mathbf{x}_{j}\right\|}\right), & \text { sum_n }_{i} \leftarrow \text { sum_n }_{i}+1, \\
\text { sum_ } \mathbf{x}_{j} \leftarrow \text { sum_ } \mathbf{x}_{j}+\frac{1}{2}\left(\mathbf{x}_{i}+\mathbf{x}_{j}-L_{e} \frac{\mathbf{x}_{i}-\mathbf{x}_{j}}{\left\|\mathbf{x}_{i}-\mathbf{x}_{j}\right\|} \|,\right. & \text { sum_n }_{j} \leftarrow \text { sum_ } n_{j}+1 .
\end{array}
\]

Finally, update each vertex as:

\[\mathbf{v}_{i} \leftarrow \mathbf{v}_{i}+\frac{1}{\Delta t}\left(\frac{0.2 \mathbf{x}_{i}+s u m_{-} \mathbf{x}_{i}}{0.2+s u m_{-} n_{i}}-\mathbf{x}_{i}\right), \quad \mathbf{x}_{i} \leftarrow \frac{0.2 \mathbf{x}_{i}+s u m_{-} \mathbf{x}_{i}}{0.2+\operatorname{sum_n} n_{i}}
\]

作者给出的 \(\alpha = 0.2f\) 可以参考最后一张图.

	void Strain_Limiting()
	{
		Mesh mesh = GetComponent<MeshFilter> ().mesh;
		Vector3[] vertices = mesh.vertices;

		//Apply PBD here.
		Vector3[] sum_x = new Vector3[vertices.Length];
		int[] num_x = new int[vertices.Length];
		for(int i=0; i<vertices.Length; i++)
        {
			sum_x[i] = new Vector3(0, 0, 0);
			num_x[i] = 0;
        }

		for(int ei = 0; ei < L.Length; ei++)
        {
			int i = E[ei * 2];
			int j = E[ei * 2 + 1];
			Vector3 xi_xj = vertices[i] - vertices[j];
			float len_ij = L[ei] / xi_xj.magnitude;

			sum_x[i] += (vertices[i] + vertices[j] + len_ij * (xi_xj)) / 2;
			sum_x[j] += (vertices[i] + vertices[j] - len_ij * (xi_xj)) / 2;
			num_x[i]++;
			num_x[j]++;
        }
		for(int i=0; i<vertices.Length; i++)
        {
			if (i == 0 || i == 20) continue;
			V[i] += ((0.2f * vertices[i] + sum_x[i]) / (num_x[i] + 0.2f) -
				vertices[i]) / t;
			vertices[i] = (0.2f * vertices[i] + sum_x[i]) / (num_x[i] + 0.2f);
        }
		mesh.vertices = vertices;
	}

image

code

using UnityEngine;
using System.Collections;

public class PBD_model: MonoBehaviour {

	float 		t= 0.0333f;
	float		damping= 0.99f;
	int[] 		E;
	float[] 	L;
	Vector3[] 	V;
	Vector3 g = new Vector3(0, -9.8f, 0);
	float r = 2.7f;

	// Use this for initialization
	void Start ()
	{
		Mesh mesh = GetComponent<MeshFilter> ().mesh;

		//Resize the mesh.
		int n=21;
		Vector3[] X  	= new Vector3[n*n];
		Vector2[] UV 	= new Vector2[n*n];
		int[] T	= new int[(n-1)*(n-1)*6];
		for(int j=0; j<n; j++)
		for(int i=0; i<n; i++)
		{
			X[j*n+i] =new Vector3(5-10.0f*i/(n-1), 0, 5-10.0f*j/(n-1));
			UV[j*n+i]=new Vector3(i/(n-1.0f), j/(n-1.0f));
		}
		int t=0;
		for(int j=0; j<n-1; j++)
		for(int i=0; i<n-1; i++)
		{
			T[t*6+0]=j*n+i;
			T[t*6+1]=j*n+i+1;
			T[t*6+2]=(j+1)*n+i+1;
			T[t*6+3]=j*n+i;
			T[t*6+4]=(j+1)*n+i+1;
			T[t*6+5]=(j+1)*n+i;
			t++;
		}
		mesh.vertices	= X;
		mesh.triangles	= T;
		mesh.uv 		= UV;
		mesh.RecalculateNormals ();

		//Construct the original edge list
		int[] _E = new int[T.Length*2];
		for (int i=0; i<T.Length; i+=3)
		{
			_E[i*2+0]=T[i+0];
			_E[i*2+1]=T[i+1];
			_E[i*2+2]=T[i+1];
			_E[i*2+3]=T[i+2];
			_E[i*2+4]=T[i+2];
			_E[i*2+5]=T[i+0];
		}
		//Reorder the original edge list
		for (int i=0; i<_E.Length; i+=2)
			if(_E[i] > _E[i + 1])
				Swap(ref _E[i], ref _E[i+1]);
		//Sort the original edge list using quicksort
		Quick_Sort (ref _E, 0, _E.Length/2-1);

		int e_number = 0;
		for (int i=0; i<_E.Length; i+=2)
			if (i == 0 || _E [i + 0] != _E [i - 2] || _E [i + 1] != _E [i - 1])
				e_number++;

		E = new int[e_number * 2];
		for (int i=0, e=0; i<_E.Length; i+=2)
			if (i == 0 || _E [i + 0] != _E [i - 2] || _E [i + 1] != _E [i - 1])
			{
				E[e*2+0]=_E [i + 0];
				E[e*2+1]=_E [i + 1];
				e++;
			}

		L = new float[E.Length/2];
		for (int e=0; e<E.Length/2; e++)
		{
			int i = E[e*2+0];
			int j = E[e*2+1];
			L[e]=(X[i]-X[j]).magnitude;
		}

		V = new Vector3[X.Length];
		for (int i=0; i<X.Length; i++)
			V[i] = new Vector3 (0, 0, 0);
	}

	void Quick_Sort(ref int[] a, int l, int r)
	{
		int j;
		if(l<r)
		{
			j=Quick_Sort_Partition(ref a, l, r);
			Quick_Sort (ref a, l, j-1);
			Quick_Sort (ref a, j+1, r);
		}
	}

	int  Quick_Sort_Partition(ref int[] a, int l, int r)
	{
		int pivot_0, pivot_1, i, j;
		pivot_0 = a [l * 2 + 0];
		pivot_1 = a [l * 2 + 1];
		i = l;
		j = r + 1;
		while (true)
		{
			do ++i; while( i<=r && (a[i*2]<pivot_0 || a[i*2]==pivot_0 && a[i*2+1]<=pivot_1));
			do --j; while(  a[j*2]>pivot_0 || a[j*2]==pivot_0 && a[j*2+1]> pivot_1);
			if(i>=j)	break;
			Swap(ref a[i*2], ref a[j*2]);
			Swap(ref a[i*2+1], ref a[j*2+1]);
		}
		Swap (ref a [l * 2 + 0], ref a [j * 2 + 0]);
		Swap (ref a [l * 2 + 1], ref a [j * 2 + 1]);
		return j;
	}

	void Swap(ref int a, ref int b)
	{
		int temp = a;
		a = b;
		b = temp;
	}

	void Strain_Limiting()
	{
		Mesh mesh = GetComponent<MeshFilter> ().mesh;
		Vector3[] vertices = mesh.vertices;

		//Apply PBD here.
		Vector3[] sum_x = new Vector3[vertices.Length];
		int[] num_x = new int[vertices.Length];
		for(int i=0; i<vertices.Length; i++)
        {
			sum_x[i] = new Vector3(0, 0, 0);
			num_x[i] = 0;
        }

		for(int ei = 0; ei < L.Length; ei++)
        {
			int i = E[ei * 2];
			int j = E[ei * 2 + 1];
			Vector3 xi_xj = vertices[i] - vertices[j];
			float len_ij = L[ei] / xi_xj.magnitude;

			sum_x[i] += (vertices[i] + vertices[j] + len_ij * (xi_xj)) / 2;
			sum_x[j] += (vertices[i] + vertices[j] - len_ij * (xi_xj)) / 2;
			num_x[i]++;
			num_x[j]++;
        }
		for(int i=0; i<vertices.Length; i++)
        {
			if (i == 0 || i == 20) continue;
			V[i] += ((0.2f * vertices[i] + sum_x[i]) / (num_x[i] + 0.2f) -
				vertices[i]) / t;
			vertices[i] = (0.2f * vertices[i] + sum_x[i]) / (num_x[i] + 0.2f);
        }
		mesh.vertices = vertices;
	}

	void Collision_Handling()
	{
		Mesh mesh = GetComponent<MeshFilter> ().mesh;
		Vector3[] X = mesh.vertices;

		//For every vertex, detect collision and apply impulse if needed.
		GameObject sphere = GameObject.Find("Sphere");
		Vector3 c = sphere.transform.position;
		//Handle colllision.
		for (int i = 0; i < X.Length; i++)
		{
			if (i == 0 || i == 20) continue;
			float distance = (X[i] - c).magnitude;
			if (distance < r)
			{
				V[i] += (c + r * (X[i] - c) / distance - X[i]) / t;
				X[i] = c + r * (X[i] - c) / distance;
			}

		}

		mesh.vertices = X;
	}

	// Update is called once per frame
	void Update ()
	{
		Mesh mesh = GetComponent<MeshFilter> ().mesh;
		Vector3[] X = mesh.vertices;

		for(int i=0; i<X.Length; i++)
		{
			if(i==0 || i==20)	continue;
			//Initial Setup
			V[i] += g * t;
			V[i] *= damping;
			X[i] += t * V[i];
		}
		mesh.vertices = X;

		for(int l=0; l<32; l++)
			Strain_Limiting ();

		Collision_Handling ();

		mesh.RecalculateNormals ();

	}

}