关于KMP

KMP算法，对于求b串在a串中出现的次数。

在学习KMP之前，希望大家充分掌握hash。

HASH：

1.hash表：用来离散化（hash数组，hash链表）

2.Rabin-Kap算法：

　　可替代KMP(O(n)),Manacher(O(n))等；
　　hs[t]=hs[t-1]*p+s[t]；
　　hash(x,y)=hs[y]-hs[x-1]*p^(y-x+1)；  
哈希是字符串题目的基础（个人觉得）

一般情况下，hash是可以替代KMP的。

但我们为什么还要学KMP呢？

众所周知，hash会产生hash冲突。于是kmp就上场了。

我们由一道题来引入正题：

很明显，次数为3（abababa）

　　有三种方法：

　　　　一、暴力　　

　　　　　　枚举左端或右端点，另一个端点根据S2确定，线性扫一遍当前区间，检查是否匹配。

　　　　　　If(匹配) ans++;
　　　　　　时间复杂度： O(n^2) 在此不再赘述。
　　　　二、哈希
　　　　　　在暴力的基础上，扫描区间检查的时候是O(1)的。
　　　　　　总时间复杂度： O(n)
　　　　三、 KMP算法
　　　　　　　而KMP算法也可以在O(n)的时间内求出答案。 
暴力匹配：

每次从A字符串的第i位，B字符串的第1位开始逐一比较，相等则继续下一位比较，如果能一直比较到B字符串的末尾，则找到了一次匹配

最坏情况：

A=aaaaaaaaaaaaaaaaaaaa 
B=aaaaaaaab 
设A的长度为N，B的长度为M

时间复杂度为O(MN)

KMP算法 
f[i]:最大的k，使得A(1..i)的子串的后k位等于B的前k位
i = 7
A = abababaababacb
B = ababacb
f[i] = 5 
B在A中出现的次数 等于 满足f[i]=(B的长度)的i的个数
转化为快速求f[i]数组

关于转化：

关于代码实现：

辅助数组next：

代码：

#include<cstdio>
#include<cstring>
using namespace std;
const int N=1e6+;
char s1[N],s2[N];
int cas,l1,l2,fail[N];
void get_next(){
    int p=;fail[]=;
    for(int i=;i<=l2;i++){
        while(p>&&s2[i]!=s2[p+]) p=fail[p];
        if(s2[i]==s2[p+]) p++;
        fail[i]=p;
    }
}
void kmp(){
    int p=,ans=;
    for(int i=;i<=l1;i++){
        while(p>&&s1[i]!=s2[p+]) p=fail[p];
        if(s1[i]==s2[p+]) p++;
        if(p==l2) ans++,p=fail[p];
    }
    printf("%d\n",ans);
}
int main(){
    for(scanf("%d",&cas);cas--;){
        scanf("%s%s",s2+,s1+);
        l1=strlen(s1+);l2=strlen(s2+);
        get_next();
        kmp();
    }
    return ;
}

关于KMP的应用：

应用1.

　　给定一个字符串A，求最短的字符串B，使得A是若干个B连接成的字符串的前缀 。

　　　　若A=abcabcab 
　　　　则B=abc 
　　解法：

　　　　求出A串在KMP算法中A的next数组
　　　　设A的长度为N
　　　　则答案为A的前N-next[N]位
　　　　显然[nxet[N]+1,N]是循环节

　　　　为什么呢？

　　　　　　我们可以分两种情况讨论：

　　　　　　　　1.next[N]>N/2

　　　　　　　　2.nextN]<=N/2

应用2.

　　给定一个字符串A，求最短的字符串B，使得A是若干个B连接成的字符串的子串

　　　　若A=bcabcabc

　　　　则B=abc

　　解法：

　　　　其实和上一题一毛一样

　　　　A=bcabcabc

　　　　若B是一个循环节，则把B循环节移位一下仍是循环节。

　　　　abc->bca

应用3：

　　给出字符串A和B，求在A中最多能选出多少个互不重叠的B串 
　　　　A=abababab

　　　　B=aba

　　　最多选出两个：abababab

　　解法：

　　　　每次贪心地选出最靠左的一个B串即可

　　　　KMP匹配时记下上次完全匹配的位置，遇到完全匹配时判断是否和上次的位置重叠即可

应用4：

　　给定一个字符串A

　　对于A的每个前缀A（1...i），求最长的字符串B_i，使得len(B_i)<i,且A是若干个B_i连接成的字符串的前缀

　　求每个B_i，len（A）<=10^6

　　解法：

　　　　将每个Bi称作循环节，最长的循环节不一定是最短循环节重复若干遍

　　　　aabbaa
　　　　最短： aabb
　　　　最长： aabba 
　　　　求next数组
　　　　对于每个前缀A(1…i)， A(1…i-next[i])， A(1…inext[next[i]])……都是它的循环节
　　　　沿着next指针往前跳，直到跳到0之前
　　　　对每个i直接跳： O(N2)
　　　　递推：记min[i]表示从i开始沿next往前跳最小能跳到多少
　　　　时间复杂度：O(N) 
应用5：

　　在N*M字符矩阵中找出一个最小子矩阵，使其多次复制所得的矩阵包含原矩阵。 N<=10000,M<=75

　　　　

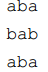
　　解法：

　　　　先找出最大的K，使得原矩阵是若干个K*M的矩阵拼成一列后的子矩阵

　　　　把一行看做一个整体，对列做KMP

　　　　用应用1的方法确定最小行宽

　　　　再在K*M的矩阵中，把一列看做一个整体，用同样的方法求最小行宽

　　　　时间复杂度：O(N*M) 
应用6：

　　字符集中有一些字符（最多26个）， 给出每个字符的出现概率（它们的和保证为1）
　　再给出一个子串B，长为M
　　求：任给一个长度为N的字符串A（只能包含字符集中的字符），使得S是A的子串的概率。
　　N<=100

　　解法：
　　　　动态规划
　　　　想象一边随机生成字符串A，一边用KMP匹配字符串B的过程
　　　　f[i][j]表示随机生成到第i位，此时B串匹配到第j位的概率
　　　　枚举下一位生成字符c，设其生成概率为gc
　　　　假设下一位填c，计算出KMP匹配指针j应该移动到j‘
　　　　f[i+1][j’] += f[i][j]*gc
　　　　已经匹配到第m位的状态不再进行转移
　　　　　　ans = ∑f[i][m]

应用7：

　　给定一个数字串A，不含前导0，长为m。 m<=9
　　　　求第P小的包含子串A的数字
　　　　P<=109 
　　解法：

　　　　答案最多18位
　　　　二分答案X，转为判断小于等于X的包含子串A的数字有多少个
　　　　F[i][j][k][l]表示，填完前i位， KMP指针指向A的第j位，之前是否出现过子串A的状态为k（0/1），下一位能否任意填数的状态为l（0/1），的方案数
　　　　答案为∑f[18][j][1][l] 
应用8：

　　有一枚硬币，抛到正面的概率是a/b，反面概率是1-a/b
　　不停地抛硬币，将得到的结果用01序列记录下来， 0表示反面， 1表示正面
　　给定01序列A，长为n，求期望抛几次可以在结果序列中找到子串A
　　n<=1000， 0<=a,b<=100
　　答案用最简分数形式输出 
　　解法：

　　　　想象一边随机生成序列一边在A串上移动KMP匹配指针的过程
　　　　f[i]表示当指针在A的第i位时， 期望抛几次可以抛出A串
　　　　设： i0为下一位抛出0时指针对应的位置， i1为下一位抛出1时指针对应的位置
　　　　f[n] = 0
　　　　f[i] = 1+p*f[i1]+(1-p)*f[i0] （i<n）
　　　　解方程组 
　　　　太麻烦（而且要求答案保留分数形式）
　　　　注意到， i0、 i1中必有一个等于i+1，另一个小于I
　　　　当i0=i+1时：f[i] = 1+(a/b)*f[i1]+(1-a/b)*f[i0]
　　　　当i1=i+1时：
　　　　f[i+1] = (b/a)*(f[i]-1-(1-a/b)*f[i0])
　　　　递推即可

一世安宁