P3587 [POI2015]POD

题目描述

长度为n的一串项链，每颗珠子是k种颜色之一。 第i颗与第i-1,i+1颗珠子相邻，第n颗与第1颗也相邻。切两刀，把项链断成两条链。要求每种颜色的珠子只能出现在其中一条链中。求方案数量（保证至少存在一种），以及切成的两段长度之差绝对值的最小值。

输入输出格式

输入格式：

第一行n,k(2<=k<=n<=1000000)。颜色从1到k标号。接下来n个数，按顺序表示每颗珠子的颜色。（保证k种颜色各出现至少一次）。

输出格式：

一行两个整数：方案数量，和长度差的最小值

输入输出样例

输入样例#1：

9 5
2 5 3 2 2 4 1 1 3

输出样例#1：

4 3

说明

长度为n的一串项链，每颗珠子是k种颜色之一。 第i颗与第i-1,i+1颗珠子相邻，第n颗与第1颗也相邻。

切两刀，把项链断成两条链。要求每种颜色的珠子只能出现在其中一条链中。

求方案数量（保证至少存在一种），以及切成的两段长度之差绝对值的最小值。

Solution：

　　本题思维题，ZYYS。

　　还记得前面HRZ学长讲的一道判断相似字符串的题目（那题做法是处理出26个字母分别为关键字的01hash值，排序后判断相等），本题做法类似，先将原数列的断点按每种颜色的出现次数求环形前缀和，因为是环形，所以最后一个该颜色的后面的断点前缀和为0，我们以样例为例：

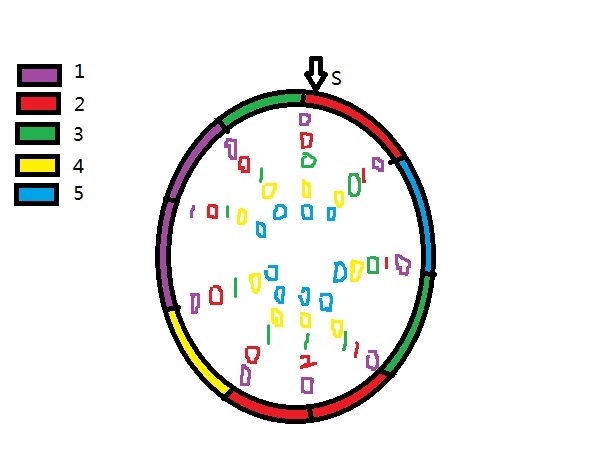　　留图带画（手绘勿喷）。

　　不难发现能切两刀的位置所对应的$k$元组一定相等，证明很简单：若这两个位置对应的$k$元组相等，那么同一颜色的环形前缀和是相等的，这就说明在这两位置切出的两段中有一段一定不包含该颜色，于是另一段一定包含所有的该颜色咯。

　　那么我们将每个位置的$k$元组处理出来，由于$k\leq 10^6$又要比较相等，所以还得hash。

　　于是第一问就迎刃而解了，只需要对hash值排序，然后组合计数。

　　第二问要求分出的两段的差的最小值，设断点为$l,r$，那么差值$=|n-2*(r-l)|$（注意$(r-l)$不用+1，因为l、r为断点标号，之间有r-l个颜色），显然要使的差值最小，就得使$r-l$尽可能接近$n/2$，满足单调性，于是直接单调队列，实现时在第一问的过程中对于hash值相等的一段处理并更新答案就好了。

　　（坑点：卡单hash，所以得双hash，然后$k$很大，所以基数也得选大，分别选两组孪生素数就OK啦！>.^_^.<）

代码：

/*Code by 520 -- 9.3*/
#include<bits/stdc++.h>
#define il inline
#define ll long long
#define RE register
#define For(i,a,b) for(RE int (i)=(a);(i)<=(b);(i)++)
#define Bor(i,a,b) for(RE int (i)=(b);(i)>=(a);(i)--)
using namespace std;
const int N=,P1=,P2=,mod1=1e9+,mod2=1e9+;
ll s1[N],s2[N],h1[N],h2[N];
int n,k,a[N],b[N],c[N];
struct node{
    int id;
    ll sum1,sum2;
    bool operator <(const node &a)const {
        if(sum1!=a.sum1)return sum1<a.sum1;
        if(sum2!=a.sum2)return sum2<a.sum2;
        return id<a.id;
    }
}t[N];

int gi(){
    int a=;char x=getchar();
    while(x<''||x>'')x=getchar();
    while(x>=''&&x<='')a=(a<<)+(a<<)+(x^),x=getchar();
    return a;
}

int main(){
    n=gi(),k=gi();
    For(i,,n) a[i]=gi();
    s1[]=s2[]=;
    For(i,,k) s1[i]=s1[i-]*P1%mod1,s2[i]=s2[i-]*P2%mod2;
    Bor(i,,n) if(!b[a[i]]) b[a[i]]=i;
    ll sum1=,sum2=;
    For(i,,n) {
        c[a[i]]++;
        sum1=(sum1+s1[a[i]])%mod1,sum2=(sum2+s2[a[i]])%mod2;
        if(b[a[i]]==i)
            sum1=(sum1-s1[a[i]]*c[a[i]]%mod1+mod1)%mod1,
            sum2=(sum2-s2[a[i]]*c[a[i]]%mod2+mod2)%mod2;
        t[i]=node{i,sum1,sum2};
    }
    sort(t+,t+n+);
    int mid=n+>>,ans=n;
    ll cnt=;
    for(RE int i=;i<=n;){
        RE int nxt=i;
        while(nxt<=n&&t[nxt].sum1==t[i].sum1&&t[nxt].sum2==t[i].sum2) nxt++;
        cnt+=1ll*(nxt-i)*(nxt-i-)/;
        for(int l=i,r=i;r<nxt;r++){
            while(l<r&&t[r].id-t[l].id>=mid)l++;
            int tp1=abs(n-*(t[r].id-t[l].id));
            if(l>i){
                int tp2=abs(n-*(t[r].id-t[l-].id));
                if(tp2<tp1)tp1=tp2;
            }
            if(tp1<ans)ans=tp1;
        }
        i=nxt;
    }
    printf("%lld %d\n",cnt,ans);
    return ;
}