poj 3013 Big Christmas Tree (最短路径Dijsktra) -- 第一次用优先队列写Dijsktra

http://poj.org/problem?id=3013

Big Christmas Tree

Time Limit: 3000MS		Memory Limit: 131072K
Total Submissions: 19009		Accepted: 4048

Description

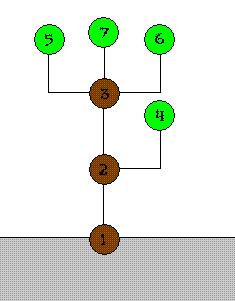Christmas is coming to KCM city. Suby the loyal civilian in KCM city is preparing a big neat Christmas tree. The simple structure of the tree is shown in right picture.

The tree can be represented as a collection of numbered nodes and some edges. The nodes are numbered 1 through n. The root is always numbered 1. Every node in the tree has its weight. The weights can be different from each other. Also the shape of every available edge between two nodes is different, so the unit price of each edge is different. Because of a technical difficulty, price of an edge will be (sum of weights of all descendant nodes) × (unit price of the edge).

Suby wants to minimize the cost of whole tree among all possible choices. Also he wants to use all nodes because he wants a large tree. So he decided to ask you for helping solve this task by find the minimum cost.

Input

The input consists of T test cases. The number of test cases T is given in the first line of the input file. Each test case consists of several lines. Two numbers v, e (0 ≤ v, e ≤ 50000) are given in the first line of each test case. On the next line, v positive integers w_i indicating the weights of v nodes are given in one line. On the following e lines, each line contain three positive integers a, b, c indicating the edge which is able to connect two nodes a and b, and unit price c.

All numbers in input are less than 2¹⁶.

Output

For each test case, output an integer indicating the minimum possible cost for the tree in one line. If there is no way to build a Christmas tree, print “No Answer” in one line.

Sample Input

2
2 1
1 1
1 2 15
7 7
200 10 20 30 40 50 60
1 2 1
2 3 3
2 4 2
3 5 4
3 7 2
3 6 3
1 5 9

Sample Output

15
1210

Source

POJ Monthly--2006.09.29, Kim, Chan Min (kcm1700@POJ)

 

【题解】：

　　变向的最短路劲问题：

　　　　　　题目意思其实就是求各点到1节点的 最短路径*节点权值 之和，根节点1的权值没有用的

【code】：

 /**
 Judge Status:Accepted      Memory:2880K
 Time:610MS      Language:G++
 Code Length:2062B  Author:cj
 */

 #include<iostream>
 #include<queue>
 #include<stdio.h>
 #include<string.h>
 #include<stdlib.h>

 #define N 50005
 #define INF 1000000000000
 using namespace std;

 struct Edge  //保存边的结构体
 {
     int to;   //边连接的另外个点
     int next;  //下一个搜索的节点
     int w;  //节点的权值
 }edge[N<<];

 struct Nod
 {
    int u;   //进入队列中的点
    __int64 dis;  //到该点的距离
 }now,temp;

 bool operator< (Nod a,Nod b)   //优先队列重载'<'运算符
 {
     return a.dis>b.dis;  //小到大
 }

 int weight[N],head[N],visit[N];
 __int64 dis[N];  //第一点到各点的最小距离

 void init(int n)  //初始化
 {
     int i;
     for(i=;i<=n;i++)
     {
         visit[i] = ;
         dis[i] = INF;
         head[i] = -;
     }
 }

 void Dijkstra(int s)
 {
     int i,v;
     dis[s] = ;
     priority_queue<Nod> p_q;  //优先队列 你懂的
     temp.dis = ;
     temp.u = s;
     p_q.push(temp);
     while(!p_q.empty())
     {
         temp = p_q.top();  //每次去的都是距离起点最小的点（优先队列的性质）
         p_q.pop();
         if(visit[temp.u])  continue;
         visit[temp.u] = ;
         for(i=head[temp.u];i!=-;i=edge[i].next)  //每次遍历跟这个点有连接的所有点
         {
             v = edge[i].to;
             if(!visit[v]&&dis[v]>dis[temp.u]+edge[i].w)
             {
                 dis[v] = dis[temp.u]+edge[i].w;  //距离更新
                 now.u = v;
                 now.dis = dis[v];
                 p_q.push(now); //压入队列
             }
         }
     }
 }

 int main()
 {
     int t;
     scanf("%d",&t);
     while(t--)
     {
         int m,n;
         scanf("%d%d",&n,&m);
         int i;
         for(i=;i<n;i++)    scanf("%d",weight+i);
         int id = ;
         init(n);
         int a,b,c;
         for(i=;i<m;i++)
         {
             scanf("%d%d%d",&a,&b,&c);
             a--,b--;
             edge[id].to = b;
             edge[id].w = c;
             edge[id].next = head[a];
             head[a] = id++;  //将边 a --> b保存

             edge[id].to = a;
             edge[id].w = c;
             edge[id].next = head[b];
             head[b] = id++;  //将边 b --> a保存
         }
         Dijkstra();
         __int64 res = ;
         for(i=;i<n;i++)
         {
             if(dis[i]==INF) break;
             res += dis[i]*weight[i];
         }
         if(i<n) puts("No Answer");
         else printf("%I64d\n",res);
     }
     return ;
 }