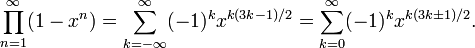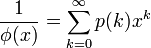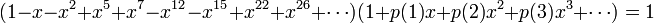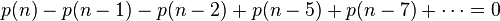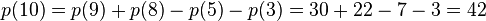2013 Multi-University Training Contest 5 Partition
思路:五边形数定理!!!
五边形数定理是一个由欧拉发现的数学定理,描述欧拉函数展开式的特性。欧拉函数的展开式如下:
亦即
欧拉函数展开后,有些次方项被消去,只留下次方项为1, 2, 5, 7, 12, ...的项次,留下来的次方恰为广义五边形数。
若将上式视为幂级数,其收敛半径为1,不过若只是当作形式幂级数(formal power series)来考虑,就不会考虑其收敛半径。
欧拉函数的倒数是分割函数的母函数,亦即:
其中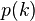 为k的分割函数。
为k的分割函数。
上式配合五边形数定理,可以得到
考虑 项的系数,在 n>0 时,等式右侧的系数均为0,比较等式二侧的系数,可得
项的系数,在 n>0 时,等式右侧的系数均为0,比较等式二侧的系数,可得
因此可得到分割函数p(n)的递归式
以n=10为例
这就是所求的了,当n<0时,p(n)=0;
p(n)的其他性质:
当限定将 表示成刚好
表示成刚好 个正整数之和时,可以表示为
个正整数之和时,可以表示为 。显然,
。显然, 。
。
- 对于
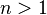 ,
,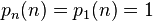
 (OEIS:A004526)
(OEIS:A004526)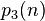 = 最接近
= 最接近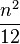 的正整数。(OEIS:A069905)
的正整数。(OEIS:A069905)
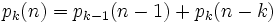
代码如下:
#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<iomanip>
#include<cmath>
#include<string>
#include<vector>
#define ll __int64
#define pi acos(-1.0)
#define MAX 100001
using namespace std;
const int mod=;
int an[MAX],n,t;
void init(){
int i,j;
an[]=an[]=;
an[]=;an[]=;an[]=;
an[]=;
for(i=;i<MAX;i++){
an[i]=;
for(j=;;j++){
int g=j*(*j-)/;
if(i-g<) break;
if(j&) an[i]+=an[i-g];
else an[i]-=an[i-g];
an[i]=an[i]%mod;
while(an[i]<) an[i]+=mod;
g=j*(*j+)/;
if(i-g<) break;
if(j&) an[i]+=an[i-g];
else an[i]-=an[i-g];
an[i]=an[i]%mod;
while(an[i]<) an[i]+=mod;
}
an[i]%=mod;
}
}
int main(){
init();
scanf("%d",&t);
while(t--){
scanf("%d",&n);
printf("%d\n",an[n]);
}
return ;
}
2013 Multi-University Training Contest 5 Partition的更多相关文章
- 2013 Multi-University Training Contest 1 Partition
这题主要是推公式…… ;}
- Integer Partition(hdu4658)2013 Multi-University Training Contest 6 整数拆分二
Integer Partition Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) T ...
- Partition(hdu4651)2013 Multi-University Training Contest 5
Partition Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Sub ...
- Partition(hdu4651)2013 Multi-University Training Contest 5----(整数拆分一)
Partition Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Sub ...
- ACM ICPC Central Europe Regional Contest 2013 Jagiellonian University Kraków
ACM ICPC Central Europe Regional Contest 2013 Jagiellonian University Kraków Problem A: Rubik’s Rect ...
- HDU 2018 Multi-University Training Contest 1 Triangle Partition 【YY】
传送门:http://acm.hdu.edu.cn/showproblem.php?pid=6300 Triangle Partition Time Limit: 2000/1000 MS (Java ...
- JSU 2013 Summer Individual Ranking Contest - 5
JSU 2013 Summer Individual Ranking Contest - 5 密码:本套题选题权归JSU所有,需要密码请联系(http://blog.csdn.net/yew1eb). ...
- HDU4888 Redraw Beautiful Drawings(2014 Multi-University Training Contest 3)
Redraw Beautiful Drawings Time Limit: 3000/1500 MS (Java/Others) Memory Limit: 65536/65536 K (Jav ...
- HDU 2018 Multi-University Training Contest 3 Problem A. Ascending Rating 【单调队列优化】
任意门:http://acm.hdu.edu.cn/showproblem.php?pid=6319 Problem A. Ascending Rating Time Limit: 10000/500 ...
随机推荐
- js 获取 当前时间 时间差 时间戳 倒计时
开发web一段时间后发现经常使用时间进行一些操作,比较多的就是获取当前时间.对时间进行比较.时间倒计时.时间戳这些部分,每次去用经常忘总是需要去查询,还是自己总结一下比较靠谱. 获取时间戳的方法: 第 ...
- 指针与strncpy---内存
指针的形式的赋值和strncpy的赋值 e.SetAttr("Amt", ToString(dAmt) ); e.SetAttr("Amt", sAm ...
- TCP/IP协议简单介绍
TCP/IP协议族总共分为四层,分别为: 应用层:应用层协议有Telnet(远程登入协议).FTP(文件传输协议).SMTP(简单邮件传送协议).SNMP(简单网络管理协议).HTT ...
- Winform DataGridView单元格的提示信息
往往当单元格的内容过多时,显示会变成这样 后缀多了几个点来显示数据未完,当鼠标移到某个单元格时,单元格里的内容会全部显示. 今天偶然发现了一个可以修改提示信息的方法,所以先记下来. 这个方法,可以对于 ...
- mouseenter 事件,固定右侧客服特效
不论鼠标指针穿过被选元素或其子元素,都会触发 mouseover 事件. 只有在鼠标指针穿过被选元素时,才会触发 mouseenter 事件. 当鼠标指针离开元素时,会发生 mouseleave 事件 ...
- mac下安装pcntl
Now you need to find out what version of PHP is installed on OSX $ php -vPHP 5.3.10 with Suhosin-Pa ...
- 转发 PHP 资料(一)
WebShell隐藏思路.webshell磁盘读写动态检测.webshell沙箱动态检测(2) 作为WebShell检测.CMS修复.WebShell攻防研究学习的第二篇文章 本文旨在研究Webs ...
- ES6学习笔记(三)
ES6加强了对Unicode的支持,并且扩展了字符串对象. 1.字符的Unicode表示法 JavaScript允许采用\uxxxx形式表示一个字符,其中"xxxx"表示字符的码点 ...
- php 微信开发之 微信支付 V3 开发 -CURLOP_TIMEOUT问题
如果不懂怎么配置的话请看文章 php 微信开发之 微信支付配置 基本配置后在继续本文章的开发 . 本文章就先继续基本的实现!也并不困难.我大概的思路的返回购买者的唯一id 和 订单号的唯一 id 就2 ...
- phpcmsv9全站搜索,不限模型
简单修改一下v9默认的搜索功能,可以不按模型搜索全站内容 下面是被修改后的search模块中的index.php文件 <?php defined('IN_PHPCMS') or exit('No ...