机器学习基石笔记:07 The VC Dimension

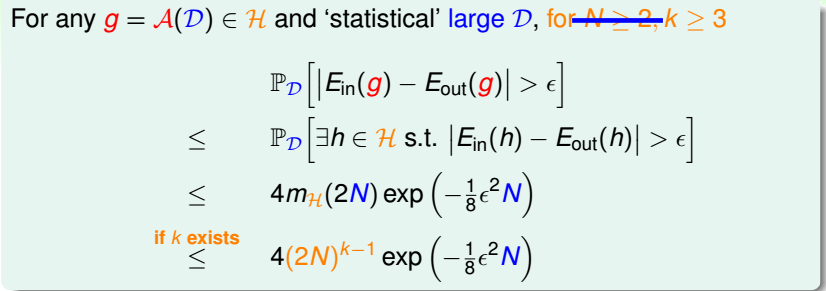












机器学习基石笔记:07 The VC Dimension的更多相关文章
- 机器学习基石:07 The VC Dimension
当N大于等于2,k大于等于3时, 易得:mH(N)被Nk-1给bound住. VC维:最小断点值-1/H能shatter的最大k值. 这里的k指的是存在k个输入能被H给shatter,不是任意k个输入 ...
- Coursera台大机器学习课程笔记6 -- The VC Dimension
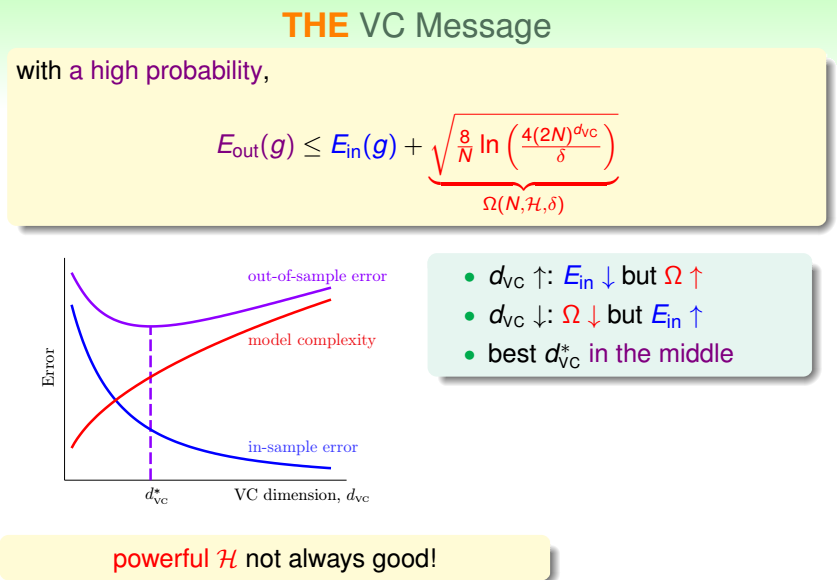
本章的思路在于揭示VC Dimension的意义,简单来说就是假设的自由度,或者假设包含的feature vector的个数(一般情况下),同时进一步说明了Dvc和,Eout,Ein以及Model C ...
- 【机器学习基石笔记】七、vc Dimension
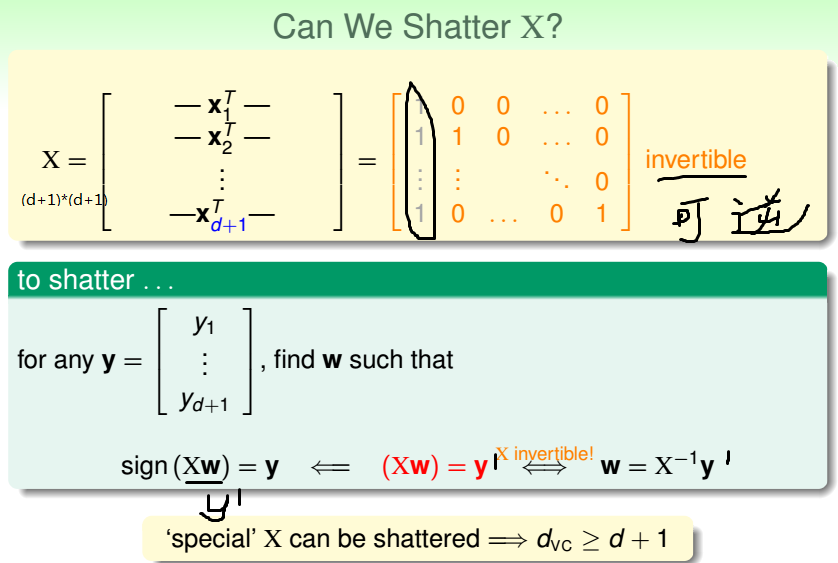
vc demension定义: breakPoint - 1 N > vc dimension, 任意的N个,就不能任意划分 N <= vc dimension,存在N个,可以任意划分 只 ...
- 【机器学习基石笔记】九、LinearRegression
[一] 线性回归直觉上的解释 得到Ein = mean(y - wx)^2 [二] w的推导 Ein = 1/N || xw - y||^2 连续.可微.凸函数 在各个方向的偏微分都是0 Ein = ...
- 07 The VC Dimension
当N大于等于2,k大于等于3时, 易得:mH(N)被Nk-1给bound住. VC维:最小断点值-1/H能shatter的最大k值. 这里的k指的是存在k个输入能被H给shatter,不是任意k个输入 ...
- 机器学习基石笔记:01 The Learning Problem
原文地址:https://www.jianshu.com/p/bd7cb6c78e5e 什么时候适合用机器学习算法? 存在某种规则/模式,能够使性能提升,比如准确率: 这种规则难以程序化定义,人难以给 ...
- 机器学习基石笔记:04 Feasibility of Learning
原文地址:https://www.jianshu.com/p/f2f4d509060e 机器学习是设计算法\(A\),在假设集合\(H\)里,根据给定数据集\(D\),选出与实际模式\(f\)最为相近 ...
- 机器学习基石笔记:08 Noise and Error
噪声:误标.对同一数据点的标注不一致.数据点信息不准确...... 噪声是针对整个输入空间的. 存在噪声的情况下,VC bound依旧有用: 存在噪声,就是f------>p(y|x),f是p的 ...
- 机器学习基石笔记:13 Hazard of Overfitting
泛化能力差和过拟合: 引起过拟合的原因: 1)过度VC维(模型复杂度高)------确定性噪声: 2)随机噪声: 3)有限的样本数量N. 具体实验来看模型复杂度Qf/确定性噪声.随机噪声sigma2. ...
随机推荐
- cmake find_package 中,include_directories,target_link_libraries 的值怎么知道?
拿Sophus库为例: find_package(Sophus REQUIRED) include_directories(${Sophus_INCLUDE_DIRS}) target_link_li ...
- C语言中 .h文件和.c文件的区别
要理解.c文件与.h文件有什么不同之处,首先需要弄明白编译器的工作过程,一般说来编译器会做以下几个过程: 1.预处理阶段 2.词法与语法分析阶段 3.编译阶段,首先编译成纯汇编语句,再将之汇编成跟CP ...
- Spring获取bean工具类,可用于在线程里面获取bean
Spring获取bean工具类,可用于在线程里面获取bean import java.util.Locale; import org.springframework.beans.BeansExcept ...
- hdoj2089(入门数位dp)
题目链接:https://vjudge.net/problem/HDU-2089 题意:给定一段区间求出该区间中不含4且不含连续的62的数的个数. 思路:这周开始做数位dp专题,给自己加油^_^,一直 ...
- MAC shell ps 命令详解(转)
ps命令为我们提供了一次性的查看进程结果,它所提供的查看结果不是动态连续的:如果想对进程时间监控,应该用top工具 Linux中的ps命令是Process Status的缩写.ps命令用来列出系统中当 ...
- ubuntu6.4系统安装JIRA-7.8
一.系统环境: system version:ubuntu6.4 openjdk version (java版本) :1.8.0_191 mysql version:14.14 jira vers ...
- 使用fabric2打包部署文件
一直以来都是复制粘贴或者拖动文件完成部署,实在是低效得很!学了学fabric,写个了脚本.如下: from fabric import Connection import shutil HOST = ...
- 20175316盛茂淞 迭代和JDB
迭代和JDB 题目 1 使用C(n,m)=C(n-1,m-1)+C(n-1,m)公式进行递归编程实现求组合数C(m,n)的功能 2 m,n 要通过命令行传入 3 提交测试运行截图(至少三张:正常如c( ...
- Event对象和触发
1.构造: //非IE浏览器事件构造方法 var event = document.createEvent('HTMLEvents');//'HTMLEvents'自定义事件名 //IE浏览器构造方法 ...
- Windows查看服务
开始→运行(Windows+R快捷键也能调出运行)→输入:services.msc→确定
