单源最短路径算法——Bellman-ford算法和Dijkstra算法
BellMan-ford算法描述
1.初始化:将除源点外的所有顶点的最短距离估计值 dist[v] ← +∞, dist[s] ←0;
2.迭代求解:反复对边集E中的每条边进行松弛操作,使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离;(运行|v|-1次)
3.检验负权回路:判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点,则算法返回false,表明问题无解;否则算法返回true,并且从源点可达的顶点v的最短距离保存在 dist[v]中。
BELLMAN-FORD(G, w, s)
INITIALIZE-SINGLE-SOURCE(G,s)
for i =1 to |G.V|-1 // 实验证明最多只需|V|-1次外层循环,|V|-1次结束后,若图G中无负权回路,那么s到其他所有顶点的最短路径求得
for each edge (u, v)∈E //算法核心,松弛每一条边,维持三角不等式成立
RELAX(u,v,w) //对每一条边进行松弛操作
for each edge (u, v)∈E //进行完|V|-1次循环操作后,如果还能某条边还能进行松弛,说明到某个点的最短路径还未找到,那么必定是存在负权回路,返回FALSE
if d[v] > d[u] + w(u, v)
return FALSE
return TRUE //若进行上面的松弛之后没有返回,说明所有的d值都不会再改变了,那么最短路径权值完全找到,返回TRUE
举例说明:
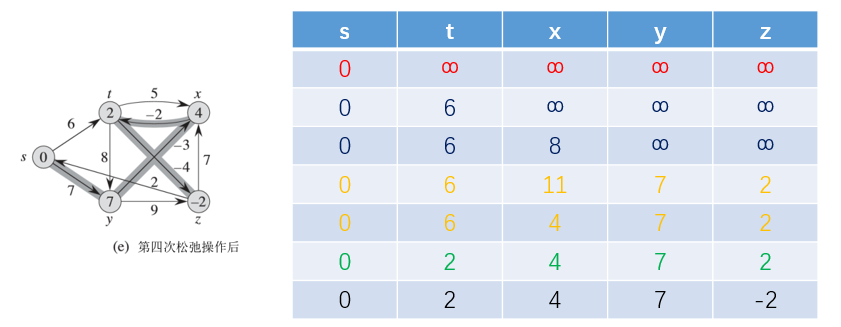
给定原点是s,初始化时候除了原点s之外,其他的都是无穷大的。因为有5个顶点,所以需要松弛的次数为5-1次
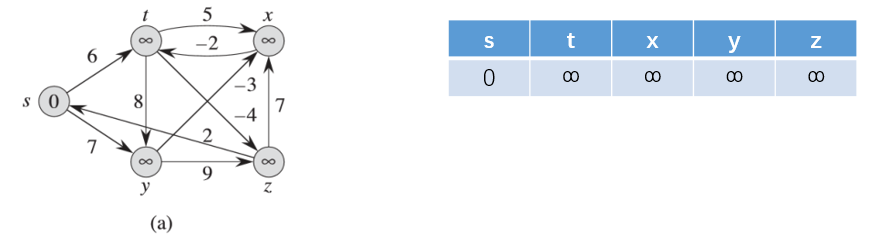
这里我们按照边<t,x>、<t,y>、<t,z>、<y,x>、<y,z>、<z,x>、<z,s>、<s,t>、<s,y>的顺序进行变得松弛操作。
第一次按照上述边进行松弛操作之后(实际上只对<s,t>、<s,y>进行操作)的结果为
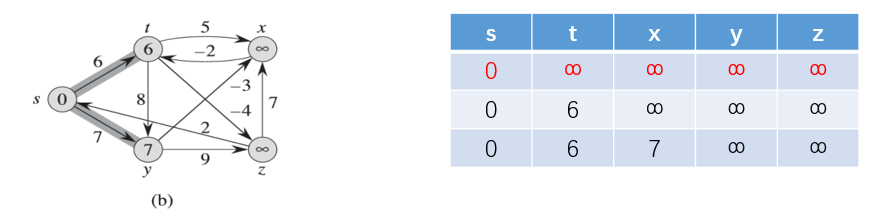
第二次按照给定边进行松弛操作之后:
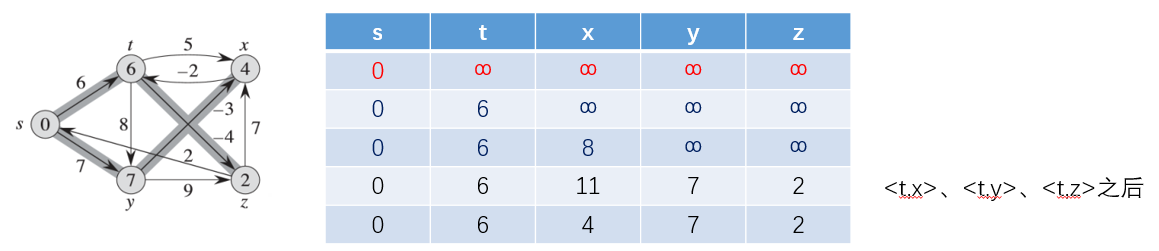
第三次松弛操作之后:
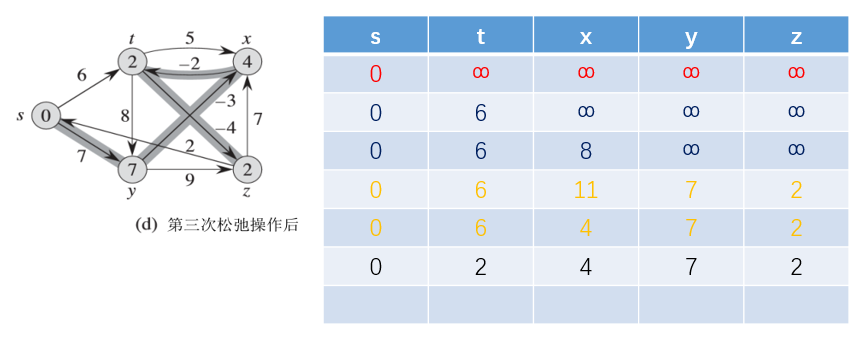
最后一次松弛操作:
给出实力代码
#include <iostream>
#include <cstdio>
using namespace std; #define INF 0xffff //权值上限
#define maxe 5000 //边数上限
#define maxn 100 //顶点数上限
int n, m; //顶点数、边数
int d[maxn]; //保存最短路径权值的数组
int parent[maxn]; //每个顶点的前驱顶点,用以还原最短路径树
struct edge //表述边的结构体,因为要对每一条边松弛
{
int u, v, w; //u为边起点,v为边端点,w为边权值,可以为负
}EG[maxe]; bool Bellman_Ford(int s) //计算从起点到所有顶点的
{
for(int i = ; i <= n; i++) //初始化操作d[EG[j].v] > d[EG[j].u]+EG[j].w
{
d[i] = INF;
parent[i] = -;
}
d[s] = ;
bool flag; //标记,判断d值是否更新,跳出外层循环的依据
for(int i = ; i < n; i++) //外层循环最多做n-1次
{
flag = false; //初始为false,假设不需再更新
for(int j = ; j < m; j++) //对m条边进行松弛操作,若有更新,flag记为true
if(d[EG[j].v] > d[EG[j].u]+EG[j].w) //if d[v] > d[u] + w(u, v),更新d[v]
{
d[EG[j].v] = d[EG[j].u]+EG[j].w;
parent[EG[j].v] = EG[j].u;
flag = true;
}
if(!flag) break; //若松弛完每条边后,flag状态不变,说明未发现更新,可直接跳出循环
}
for(int i = ; i < m; i++) //做完上述松弛后,如果还能松弛,说明存在负权回路,返回false
if(d[EG[i].v] > d[EG[i].u]+EG[i].w)
return false;
return true; //不存在负权回路,返回true
} int main()
{
int st;
printf("请输入n和m:\n");
scanf("%d%d", &n, &m);
printf("请输入m条边(u, v, w):\n");
for(int i = ; i < m; i++)
scanf("%d%d%d", &EG[i].u, &EG[i].v, &EG[i].w);
printf("请输入起点:");
scanf("%d", &st);
if(Bellman_Ford(st))
{
printf("不存在负权回路。\n");
printf("源顶点到各顶点的最短路径权值为:\n");
for(int i = ; i <= n; i++)
printf("%d ", d[i]);
printf("\n");
}
}
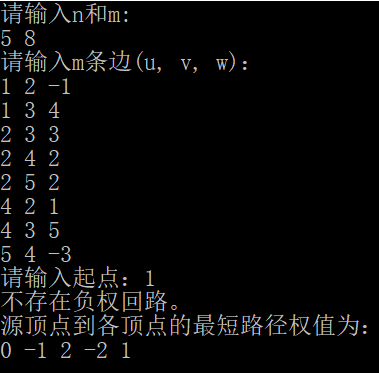
输入测试用例
1 2 -1
1 3 4
2 3 3
2 4 2
2 5 2
4 2 1
4 3 5
5 4 -3
Dijkstra算法
(1)该算法要求所有边的权重均为非负值,即对于所有的边(u,v)∈E,ω(u,v)≥0,—— 既不能有负权重的边,更 不能 有负权重的环。算法在运行过程中维持的关键信息是一组结点集合S。从源结点s到该集合中每个节点之间的最短路径已经被找到。算法重复的从结点集合V-S中选择最短路径估计最小的结点u,将u加入到集合S中,然后对所有从u发出的边进行松弛操作。
(2)算法设计思想如下:

(3)算法描述伪代码如下:

(4)下面给出算法一些理解:
上述算法第一行执行的是d值和π值的初始化,第2行将集合S初始化为一个空集。算法所维持的循环不变式为Q=V-S,不变式在算法的while循环中保持不变。
第3行对最小优先队列进行初始化,将所有的结点V都放在队列里面。此时的S=∅。
在执行while循环的时候,从集合Q=V-S中抽取结点u,第6行将该结点加入到结合S里面,从而保持不变式成立。
然后将从u结点出发的所有结点进行松弛操作。如果一条经过结点u的路径能够使得从源结点s到结点v的最短路径权重比当前的估计值更小,就对v.d的数值和前驱结点进行更新操作。
(5)下面是一个实例
输入G,源结点1,结点集合V=<1,2,3,4,5,6>
①从源结点开始,此时集合S中只有结点1,从1出发的结点有6、2,所以更新此时的dist[2]和dist[6]的数值

②选择dist[2]和dist[6]中最小的值,即dist[6]=3,将结点6加入到集合S中,然后从更新结点6出发的结点2、5、4的路径值,分别更新为dist[2] = 5、dist[5] = 4、dist[4] = 9。
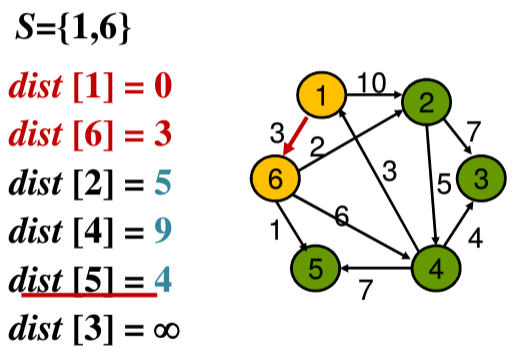
③选择dist[2] = 5、dist[5] = 4、dist[4] = 9中最小的值,即dist[5] = 4,将结点5加入到结合S中,然后更新从结点5出发的结点的值,由于没有从结点5出发的结点,所以直接进行下一步
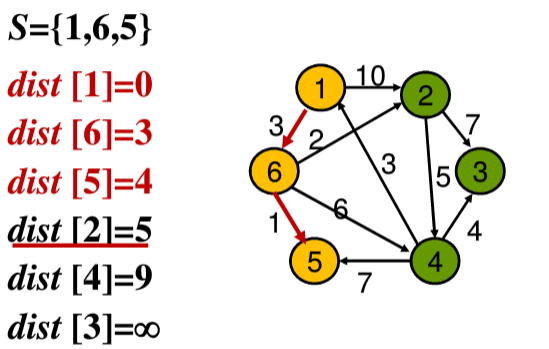
④第三步中选择dist[2] = 5,将结点2加入集合S中,然后更新从结点2出发的结点3、4的值,分别为dist[3] = 12、dist[4] = 9
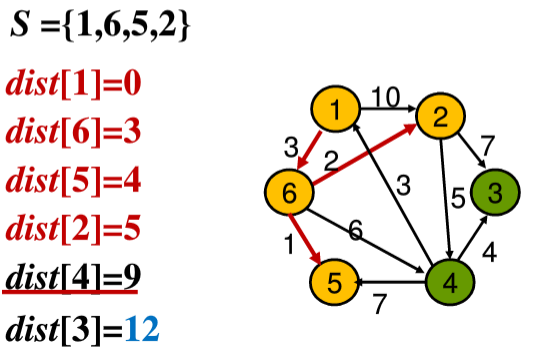
⑤从剩下的两个结点3、4中选择dist更小的结点4,将结点4加入集合S中,然后更新从结点4出发的结点3的值,判断之后,发现dist[3]依旧还是12
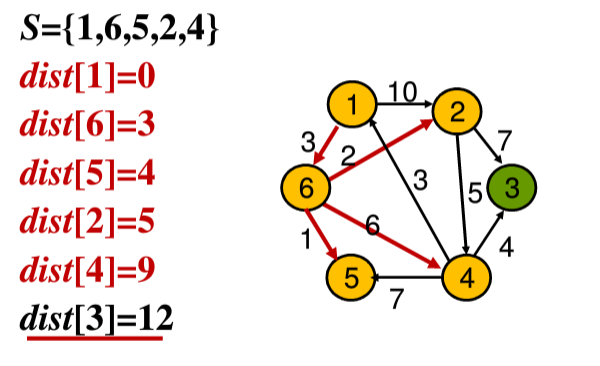
⑥最后一步,将结点3加入集合S中,此时以及更新完毕,找到了从结点1到达所有节点的最短路径
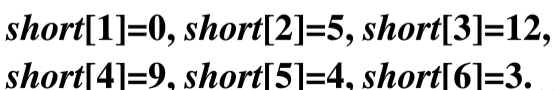
单源最短路径算法——Bellman-ford算法和Dijkstra算法的更多相关文章
- P3371 【模板】单源最短路径(弱化版)(Dijkstra算法)
题目描述 如题,给出一个有向图,请输出从某一点出发到所有点的最短路径长度. 输入输出格式 输入格式: 第一行包含三个整数N.M.S,分别表示点的个数.有向边的个数.出发点的编号. 接下来M行每行包含三 ...
- Prim算法和Dijkstra算法的异同
Prim算法和Dijkstra算法的异同 之前一直觉得Prim和Dijkstra很相似,但是没有仔细对比: 今天看了下,主要有以下几点: 1: Prim是计算最小生成树的算法,比如为N个村庄修路,怎么 ...
- 字符串查找算法总结(暴力匹配、KMP 算法、Boyer-Moore 算法和 Sunday 算法)
字符串匹配是字符串的一种基本操作:给定一个长度为 M 的文本和一个长度为 N 的模式串,在文本中找到一个和该模式相符的子字符串,并返回该字字符串在文本中的位置. KMP 算法,全称是 Knuth-Mo ...
- 词性标注算法之CLAWS算法和VOLSUNGA算法
背景知识 词性标注:将句子中兼类词的词性根据上下文唯一地确定下来. 一.基于规则的词性标注方法 1.原理 利用事先制定好的规则对具有多个词性的词进行消歧,最后保留一个正确的词性. 2.步骤 ①对词性歧 ...
- 贪心算法-最小生成树Kruskal算法和Prim算法
Kruskal算法: 不断地选择未被选中的边中权重最轻且不会形成环的一条. 简单的理解: 不停地循环,每一次都寻找两个顶点,这两个顶点不在同一个真子集里,且边上的权值最小. 把找到的这两个顶点联合起来 ...
- 【页面置换算法】LRC算法和FIFS算法
算法介绍 FIFO:该算法总是淘汰最先进入内存的页面,即选择在内存中驻留时间最久的页面予以淘汰.该算法实现简单,只需把一个进程已调入内存的页面,按先后次序链接成一个队列,并设置一个指针,称为替换指针, ...
- 洛谷 P4779 :【模板】单源最短路径(标准版)(Dijkstra+堆优化+链式前向星)
题目背景 2018 年 7 月 19 日,某位同学在 NOI Day 1 T1 归程 一题里非常熟练地使用了一个广为人知的算法求最短路. 然后呢? 100→60: Ag→Cu: 最终,他因此没能与理想 ...
- SQL的循环嵌套算法:NLP算法和BNLP算法
MySQL的JOIN(二):JOIN原理 表连接算法 Nested Loop Join(NLJ)算法: 首先介绍一种基础算法:NLJ,嵌套循环算法.循环外层是驱动表,循坏内层是被驱动表.驱动表会驱动被 ...
- 编程实现prim算法和Dijkstra算法。
网址链接:http://blog.csdn.net/anialy/article/details/7603170
随机推荐
- 子页面调整父亲页面的iframe元素
$('iframe', parent.document).attr('scrolling','no');
- 4-29 c语言之栈,队列,双向链表
今天学习了数据结构中栈,队列的知识 相对于单链表来说,栈和队列就是添加的方式不同,队列就相当于排队,先排队的先出来(FIFO),而栈就相当于弹夹,先压进去的子弹后出来(FILO). 首先看一下栈(St ...
- JMeter处理返回结果unicode转码为中文
问题举例: { "ServerCode":"200","ServerMsg":"\u6210\u529f"," ...
- 最适合入门的Laravel中级教程(二)用户认证
之前的初级教程主要是学习简单的增删改查: 接着的中级教程的目标是在初级教程的基础上能写出更复杂更健壮的程序: 我们先来学习 laravel 的用户认证功能: 在现代网站中基本都有用户系统: 而我们每开 ...
- python 函数的名称空间及作用域
一:名称空间 1:什么是名称空间: 名称空间即:储存名字与值的内存地址关联关系的空间 2.名称空间的分类: 内置名称空间:存储器自带的一些名称与值的对应关系,如:print,len,max等; 生命周 ...
- NLTK 统计词频
import nltk Freq_dist_nltk = nltk.FreqDist(list) for k,y in Freq_dist_nltk: print str(k),str(y)
- C++11 constexpr常量表达式
常量表达式函数 要求: 函数体内只有单一的return返回语句 例如: constexpr int data() { const int i=1; //含有除了return以外的语句 return i ...
- mysql学习笔记--数据库操作
一.显示数据库 show databases; 二.创建数据库 create database [if not exists] 数据库名 [字符编码] 注意: a. 如果已经存在数据库再创建会报错 b ...
- webpack浅析---出口篇
webpack有四个核心概念: 入口(entry) 输出(output) loader 插件(plugins) 输出: 在哪里输出创建的bundles,以及如何命名这些文件, 默认./dist fil ...
- CRM中QueryDict和模型表知识补充
CRM中QueryDict和模型表知识补充 1.QueryDict的用法 request.GET的用法:1.在页面上输入:http://127.0.0.1:8000/index/print(reque ...
