A Tutorial on Energy-Based Learning

目录

• 概
• 主要内容
  • 损失函数
    • Energy Loss
    • Generalized Perceptron Loss
    • Generalized Margin Loss
      • Hinge Loss
      • Log Loss
      • LVQ2 Loss
      • MCE Loss
      • Square-Square Loss
      • Square-Exponential
    • Negative Log-Likelihood Loss
      • Empirical Error Loss
  • 好的损失应该满足的一些条件
    • 条件1
    • 条件2
    • 条件3

LeCun Y., Chopra S., Hadsell R., Ranzato M. & Huang F. A Tutorial on Energy-Based Learning. To appear in “Predicting Structured Data, 2006, 1: 0.

概

从能量的角度看一些函数, 这里就记录一下这些损失.

主要内容

\(E(Y, X)\)反映了\(X, Y\)的关系, 认为能量越低, 而且的关系越紧密, 从下图中可以发现, \(X, Y\)的组合多种多样.

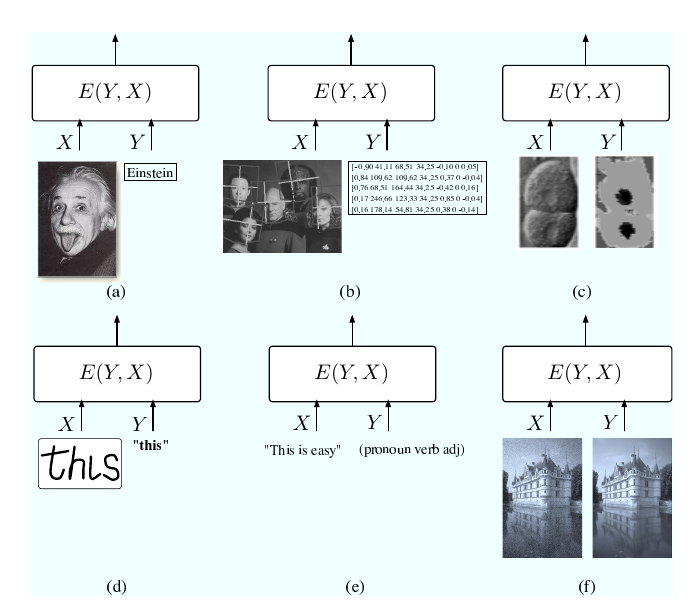
通常情况下, 我们需要训练一个映射, 其参数为\(W\), 一个好的参数可以使得

\[E(W, Y, X)
\]

很小. 不过我们通常会选取一些损失函数, 来间接最小化上面的能量函数

\[\mathcal{L}(E, S) = \frac{1}{P} \sum_{i=1}^P L(Y^i, E(W, \mathcal{Y}, X^i)) + R(W),
\]

其中\(R(W)\)是正则化项. 自然, 损失函数至少需要满足其最优点是最小化损失函数的, 当然应该还有一些其他的条件.

如果\(\mathcal{Y}\)是离散的, 我们可以令

\[\bar{Y}^i = \arg \min_{Y \in \mathcal{Y}, Y \not= Y^i} E(W, Y, X^i),
\]

相应的连续情况下

\[\bar{Y}^i = \arg \min_{Y \in \mathcal{Y}, \|Y-Y^i\| > \epsilon} E(W, Y, X^i),
\]

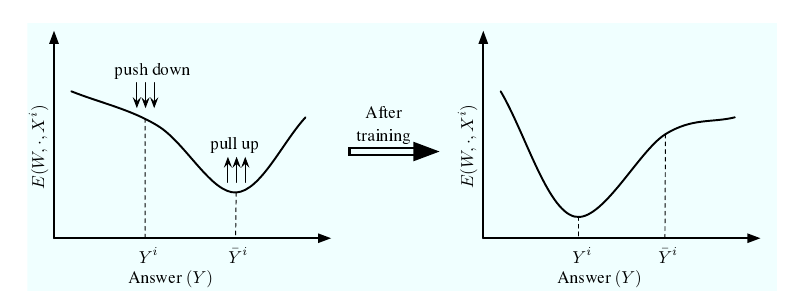
即\(\bar{Y}\)是我们最不爽的点. 很自然, 我们希望损失函数将我们希望的点\(Y^i\)的能量降低, 而拔高我们讨厌的\(\bar{Y}^i\)的能量.

损失函数

Energy Loss

\[L_{energy} (Y^i, E(W, \mathcal{Y}, X^i)) = E(W, Y^i, X^i).
\]

Generalized Perceptron Loss

\[L_{perceptron} (Y^i, E(W, \mathcal{Y}, X^i)) = E(W, Y^i, X^i) - \min_{Y \in \mathcal{Y}} E(W, Y, X^i).
\]

Generalized Margin Loss

Hinge Loss

\[L_{hinge} (W, Y^i, X^i) = \max(0, m+E(W, Y^i, X^i) - E(W, \bar{Y}^i, X^i)).
\]

Log Loss

\[L_{log} (W, Y^i,X^i) = \log (1+e^{E(W, Y^i, X^i)-E(W, \bar{Y}^i, X^i)}).
\]

LVQ2 Loss

\[L_{lvq2}(W, Y^i, X^i) = \min (1, \max(0, \frac{E(W, Y^i, X^i)- E(W, \bar{Y}^i, X^i)}{\delta E(W, \bar{Y}^i, X^i)})).
\]

虽然LVQ2 Loss和上面的非margin loss一样, 似乎是没margin的, 但是作者说最后二者有一个饱和的比例\(1+\delta\), 但是不是特别理解.

MCE Loss

\[L_{mce} (W, Y^i, X^i) = \sigma (E(W, Y^i, X^i)-E(W, \bar{Y}^i, X^i)),
\]

其中\(\sigma\)是sigmoid.

Square-Square Loss

\[L_{sq-sq} (W, Y^i, X^i) = E(X, Y^i, X^i)^2 + (\max(0, m-E(W, \bar{Y}^i, X^i)))^2.
\]

Square-Exponential

\[L_{sq-exp} (W, Y^i, X^i) = E(W, Y^i, X^i)^2 + \gamma e^{-E(W,\bar{Y}^i, X^i)}.
\]

Negative Log-Likelihood Loss

\[L_{nll}(W, Y^i, X^i) = E(W, Y^i, X^i) + \mathcal{F}_{\beta} (W, \mathcal{Y}, X^i),
\]

其中

\[\mathcal{F}_{\beta}(W, \mathcal{Y}, X^i) = \frac{1}{\beta} \log (\int_{y \in \mathcal{Y}} \exp (-\beta E(W, y, X^i))).
\]

Empirical Error Loss

\[L_{mee} (W, Y^i, X^i) = 1 - \frac{e^{-\beta E(W, Y^i, X^i)}}{\int_{y \in \mathcal{Y}}e^{-\beta E(W, y, X^i)}}.
\]

好的损失应该满足的一些条件

都是充分条件, 所以不满足也有可能是满足所需要的性质的.

条件1

对于样本\((X^i, Y^i)\), 如果预测满足

\[E(W, Y^i, X^i) < E(W, Y, X^i), \quad \forall Y \in \mathcal{Y} \: and \: Y \not = Y^i.
\]

则推断结果应当为\(Y^i\).

条件2

对于变量\(Y\)以及样本\((X^i, Y^i)\)和margin \(m\), 若

\[E(W, Y^i, X^i) < E(W, \bar{Y}, X^i) - m,
\]

则推断结果应当为\(Y^i\).

条件3

这个条件就用语言描述吧.

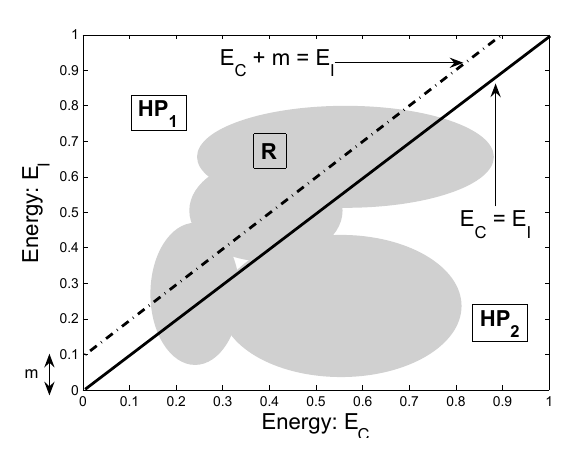
即， 要求\(HP_1\)与可行域\(R\)的交集中存在一解, 是的\((X^i, Y^i)\)在该点处的能量比\(HP_2\)与\(R\)交集的所有解的能量都要小, 其中

\[HP_1: E_C+m < E_I \\
HP_2: E_C + m > E_I.
\]

\(E_C=E(W, Y^i, X^i)\), \(E_I=E(W, \bar{Y}^i, X^i)\).

下图给出了满足上述三个条件的损失及其对应的\(m\).