selenium基本使用,及cannot find chrome binary解决方案

什么是selenium？

1. Selenium是一个用于Web应用程序测试的工具。
2. Selenium 测试直接运行在浏览器中，就像真正的用户在操作一样。
3. 支持通过各种driver（FirfoxDriver，IternetExplorerDriver，OperaDriver，ChromeDriver）驱动真实浏览器完成测试。
4. selenium也是支持无界面浏览器操作的。

为什么使用selenium？

1. 模拟浏览器功能，自动执行网页中的js代码，实现动态加载

如何安装selenium？

1. 操作谷歌浏览器驱动下载地址,　http://chromedriver.storage.googleapis.com/index.html
2. 谷歌驱动和谷歌浏览器版本之间的映射表,　http://blog.csdn.net/huilan_same/article/details/51896672
3. 查看谷歌浏览器版本,　谷歌浏览器右上角‐‐>帮助‐‐>关于
4. pip install selenium

selenium的使用步骤？

　　导入：from selenium import webdriver

　　创建谷歌浏览器操作对象：

　　　　path = 谷歌浏览器驱动文件路径

　　　　browser = webdriver.Chrome(path)

　　访问网址

　　　　url = 要访问的网址 　

　　　　browser.get(url) 

---

查看浏览器版本

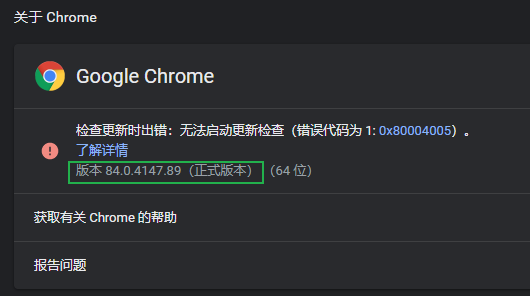
下载chrome的对应版本chromedriver.exe

使用国内源地址http://npm.taobao.org/mirrors/chromedriver/

下载好解压到文件夹，随意路径即可

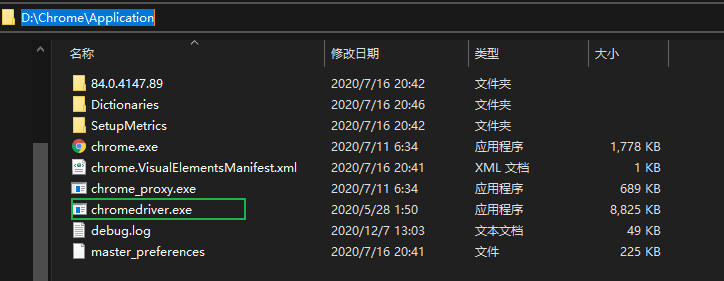
浏览器不是默认安装路径。调用Chrome浏览器时，经常会遇到以下报错cannot find chrome binary（找不到chrome文件）

需要添加浏览器到环境变量中

右击桌面chrom图标—>打开‘文件所在位置’—>复制路径—>添加到系统变量path中

# (1) 导入selenium
from selenium import webdriver
 
# 指定chromedriver.exe驱动绝对路径
path = r'D:\Chrome\Application\chromedriver.exe'
 
# (2) 创建浏览器操作对象
browser = webdriver.Chrome(path)
 
# (3) 访问网站
# url = 'https://www.baidu.com'
# 打开网页
# browser.get(url)
 
url = 'https://www.jd.com/'
 
browser.get(url)
 
# page_source方法获取网页源码
content = browser.page_source
print(content)

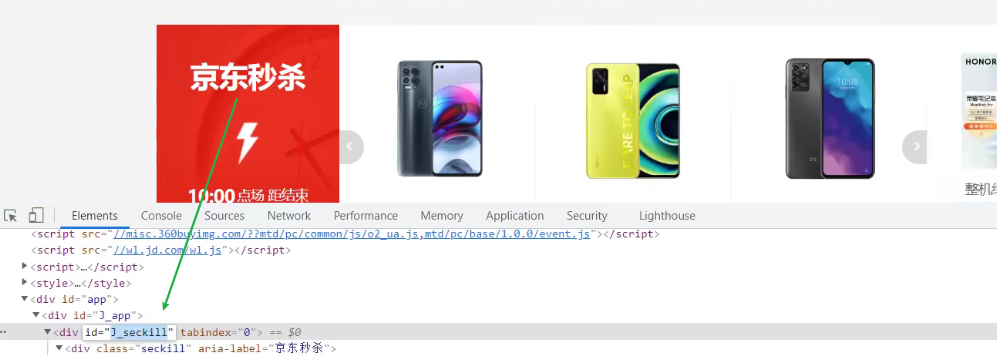
seckill是由js渲染出来的，而js要在浏览器中运行，通过urllib.request.urlopen(url)模拟浏览器发出请求对象无法获得