Solution -「CF 848D」Shake It!

\(\mathcal{Description}\)

  Link.

  初始有一个有向图 \(G=(V,E)\)，\(V=\{s,t\}\)，\(E=\langle s,t\rangle\)，一次操作定义为取任意 \(\langle u,v\rangle\in E\)，设 \(w\) 为一个新结点，则令 \(V=V\cup\{w\}\)，\(E=E\cup \{\langle u,w\rangle,\langle w,v\rangle\}\)。现进行 \(n\) 次操作，求最终有多少个本质不同的 \(G\)，满足 \(\operatorname{cut}(s,t)=m\)，答案对 \((10^9+7)\) 取模。

  \(G\) 与 \(G'\) 本质相同：存在一个 \(s,t\) 均为不动点的 \(f:V_G\rightarrow V_{G'}\)，使得 \(f\) 作用于 \(G\) 后有 \(E_G=E_{G'}\)。

  \(n,m\le50\)。

\(\mathcal{Solution}\)

  灵性的 DP 神题。

  我们称一次选取 \(\langle u,v\rangle\) 边的操作为对 \(\langle u,v\rangle\) 的扩展。

  令 \(f(i,j)\) 表示 \(i\) 次操作使原图的最大流为 \(j\) 的方案数，可见 \(f(n,m)\) 为答案；同时令 \(F(i,j)\) 为其第二维后缀和，即 \(F(i,j)=\sum_{k\ge j}f(i,j)\)。

  然后不难发现完全转移不了。 再令 \(g(i,j)\) 表示对于任意边 \(\langle u,v\rangle\)，\(i\) 次操作，扩展且仅扩展 \(\langle u,v\rangle\) 一次，使得 \(u\) 到 \(v\) 的最大流增加 \(j\)（变为 \(j+1\)）的方案数；同理定义 \(G(i,j)\)。注意 \(g\) 与 \(f\) 的区别，例如对于下图中的 <绿点, 红点>：

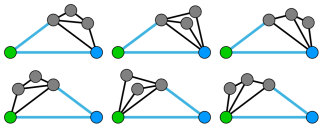
上图的方案都是 \(g(3,1)\) 所包含的，而

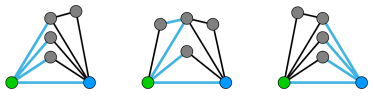
都不是 \(g(4,3)\) 所包含的，因为它们都扩展了 <绿点, 蓝点> 这条边多于一次。

  接着考虑 \(f\) 与 \(g\) 的关系，有

\[G(i,j)=\sum_{k\in[0,i)}F(k,j)F(i-k-1,j)
\]

即，先用一次操作扩展初始的 \(\langle u,v\rangle\)，此后 \(\langle u,w\rangle,\langle w,v\rangle\) 都成为 \(f\) 的子问题，只要使两者的最大流同时不小于 \(j\)，则 \(u\) 到 \(v\) 增加的流也不小于 \(j\)。并且由于 \(u,v\) 在映射中不动，所有方案均本质不同。

  难点在于对 \(f\) 的转移。我们要选取若干个 \(g\) 作用在初始的 \(\langle s,t\rangle\)，形成最终的图 \(G\)，同时保证方案本质不同。即，找到 \(g(i_1,j_1,),g(i_2,j_2),\cdots,g(i_s,j_s)\)，使得 \(\sum i=n\) 且 \(\sum j=m-1\)（\(s\) 到 \(t\) 本身就有 \(1\) 的流）。那么，在转移过程中，仅需考虑在选择方案的末尾加入 \(k\) 个当前的 \(g(i,j)\)，\(k\) 个 \(g(i,j)\) 内部的方案用隔板法可知为 \(\binom{g(i,j)+k}{k}\)，再乘上原有方案数即可。因为不同 \(g\) 之间钦定无序，相同 \(g\) 之间隔板法保证无序，故方案无序，即本质不同。

  到此，复杂度 \(\mathcal O(n^4\ln n)\)，瓶颈在于枚举“\(k\) 个当前的 \(g(i,j)\)”。

\(\mathcal{Code}\)

  代码中 f[][] 对应 \(F\)，g[][] 对应 \(G\)，h[][] 对应稍作下标移动的 \(f\)。

/* Clearink */

#include <cstdio>

#define rep( i, l, r ) for ( int i = l, repEnd##i = r; i <= repEnd##i; ++i )
#define per( i, r, l ) for ( int i = r, repEnd##i = l; i >= repEnd##i; --i )

const int MAXN = 50, MOD = 1e9 + 7;
int n, m, ifac[MAXN + 5];

inline int imin( const int a, const int b ) { return a < b ? a : b; }
inline int mul( const long long a, const int b ) { return a * b % MOD; }
inline int sub( int a, const int b ) { return ( a -= b ) < 0 ? a + MOD : a; }
inline void subeq( int& a, const int b ) { ( a -= b ) < 0 && ( a += MOD ); }
inline int add( int a, const int b ) { return ( a += b ) < MOD ? a : a - MOD; }
inline void addeq( int& a, const int b ) { ( a += b ) >= MOD && ( a -= MOD ); }
inline int mpow( int a, int b ) {
	int ret = 1;
	for ( ; b; a = mul( a, a ), b >>= 1 ) ret = mul( ret, b & 1 ? a : 1 );
	return ret;
}

inline void init() {
	int& t = ifac[MAXN] = 1;
	rep ( i, 1, MAXN ) t = mul( t, i );
	t = mpow( t, MOD - 2 );
	per ( i, MAXN - 1, 0 ) ifac[i] = mul( ifac[i + 1], i + 1 );
}

int f[MAXN + 5][MAXN + 5], g[MAXN + 5][MAXN + 5], h[MAXN + 5][MAXN + 5];

int main() {
	init();
	scanf( "%d %d", &n, &m );

	f[0][1] = h[0][0] = 1;
	rep ( i, 1, n ) {
		rep ( j, 1, i + 1 ) {
			int& crg = g[i][j];
			rep ( k, 0, i - 1 ) {
				addeq( crg, mul( f[k][j], f[i - k - 1][j] ) );
			}
		}

		rep ( j, 1, i + 1 ) {
			int gv = sub( g[i][j], g[i][j + 1] );
			per ( a, n, 0 ) per ( b, n + 1, 0 ) {
				int crh = 0;
				for ( int k = 0, si = 0, sj = 0, up = 1;
					si <= a && sj <= b; ++k, si += i, sj += j ) {

					addeq( crh, mul( h[a - si][b - sj], mul( up, ifac[k] ) ) );
					up = mul( up, add( gv, k ) );
				}
				h[a][b] = crh;
			}
		}

		per ( j, i + 1, 1 ) {
			f[i][j] = add( h[i][j - 1], f[i][j + 1] );
		}
	}

	printf( "%d\n", sub( f[n][m], f[n][m + 1] ) );
	return 0;
}