【BZOJ 3218】 3218: a + b Problem（最小割+可持久化线段树）

3218: a + b Problem

Time Limit: 20 Sec  Memory Limit: 40 MB
Submit: 1440  Solved: 545

Description

Input

Output

Sample Input

Sample Output

HINT

Source

【分析】

　　这题建图很神哦！

　　其实只是边的合并。

　　就是说，原本海陆型建图就好了的。

　　

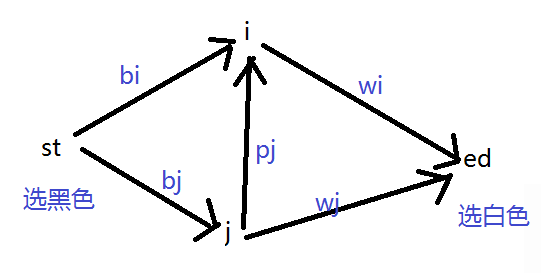
　　但是这样有一点问题，就是pj只算一次的，但是这样跑算了很多次。

　　改一改图。

　　

　　这样就好了。

　　但是边很多。

　　一开始没注意那个l~r的，就觉得嗯，开一些辅助点合并一下边。

　　后来发现还有l~r的限制，其实也是开一些辅助点合并一下边，但是这里就有点高级了。

　　就是值考虑l<=a<=r的话就是开个权值线段树然后用线段树上的点作为辅助点。

　　但是还有一个条件是i<=j的时候才算，所以是可持久化线段树。

　　关于辅助点，其实上面的j‘就是辅助点，照着做就好了。

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<queue>
 using namespace std;
 #define Maxn 5010
 #define Maxm 1000000000
 // #define Maxm 10
 #define INF 0x7fffffff
 // #define LL long long

 int mymin(int x,int y) {return x<y?x:y;}

 struct node
 {
     int x,y,f,o,next;
 }t[Maxn*];
 int len,first[Maxn*];

 void ins(int x,int y,int f)
 {
     if(y==) return;
     t[++len].x=x;t[len].y=y;t[len].f=f;
     t[len].next=first[x];first[x]=len;t[len].o=len+;
     t[++len].x=y;t[len].y=x;t[len].f=;
     t[len].next=first[y];first[y]=len;t[len].o=len-;
 }

 int dis[Maxn*],st,ed;
 queue<int > q;
 bool bfs()
 {
     memset(dis,-,sizeof(dis));
     while(!q.empty()) q.pop();
     dis[st]=;q.push(st);
     while(!q.empty())
     {
         int x=q.front();
         for(int i=first[x];i;i=t[i].next) if(t[i].f>)
         {
             int y=t[i].y;
             if(dis[y]==-)
             {
                 dis[y]=dis[x]+;
                 q.push(y);
             }
         }
         q.pop();
     }
     if(dis[ed]==-) return ;
     return ;
 }

 int ffind(int x,int flow)
 {
     if(x==ed) return flow;
     int now=;
     for(int i=first[x];i;i=t[i].next) if(t[i].f>)
     {
         int y=t[i].y;
         if(dis[y]==dis[x]+)
         {
             int a=ffind(y,mymin(flow-now,t[i].f));
             t[i].f-=a;
             t[t[i].o].f+=a;
             now+=a;
         }
         if(now==flow) break;
     }
     if(now==) dis[x]=-;
     return now;
 }

 int ans=;
 void max_flow()
 {
     while(bfs())
     {
         ans-=ffind(st,INF);
     }
 }
 void output()
 {
     for(int i=;i<=len;i+=)
     {
         printf("%d -> %d %d\n",t[i].x,t[i].y,t[i].f);
     }printf("\n");
 }

 int rt[Maxn],cnt;
 struct nnode
 {
     int lc,rc;
 }tr[Maxn*];

 void add(int l,int r,int x,int y,int a,int id)
 {
     ins(y,x,INF);
     ins(y,id,INF);
     if(l==r) return;
     int mid=(l+r)>>;
     if(a<=mid)
     {
         tr[y].lc=++cnt;tr[y].rc=tr[x].rc;
         add(l,mid,tr[x].lc,tr[y].lc,a,id);
     }
     else
     {
         tr[y].rc=++cnt;tr[y].lc=tr[x].lc;
         add(mid+,r,tr[x].rc,tr[y].rc,a,id);
     }
 }

 void add2(int l,int r,int x,int al,int ar,int id)
 {
     if(l==al&&r==ar)
     {
         ins(id,x,INF);
         return;
     }
     int mid=(l+r)>>;
     if(ar<=mid) add2(l,mid,tr[x].lc,al,ar,id);
     else if(al>mid) add2(mid+,r,tr[x].rc,al,ar,id);
     else
     {
         add2(l,mid,tr[x].lc,al,mid,id);
         add2(mid+,r,tr[x].rc,mid+,ar,id);
     }
 }

 int main()
 {
     int n;
     scanf("%d",&n);
     st=n*+,ed=st+;cnt=ed;
     rt[]=;
     len=;
     memset(first,,sizeof(first));
     for(int i=;i<=n;i++)
     {
         int a,b,c,w,al,ar,p;
         scanf("%d%d%d%d%d%d",&a,&b,&w,&al,&ar,&p);
         ans+=b+w;
         ins(st,i,b);ins(i,ed,w);
         ins(i,i+n,p);
         rt[i]=++cnt;
         add(,Maxm,rt[i-],rt[i],a,i);
         add2(,Maxm,rt[i],al,ar,i+n);
     }
     // output();
     max_flow();
     printf("%d\n",ans);
     return ;
 }

2017-04-06 22:05:14