liblinear参数及使用方法（原创）

开发语言：JAVA

开发工具：eclipse (下载地址 http://www.eclipse.org/downloads/)

liblinear版本：liblinear-1.94.jar （下载地址：http://liblinear.bwaldvogel.de/）

更多信息请参考：http://www.csie.ntu.edu.tw/~cjlin/liblinear/

1.下载 liblinear-1.94.jar，导入工程

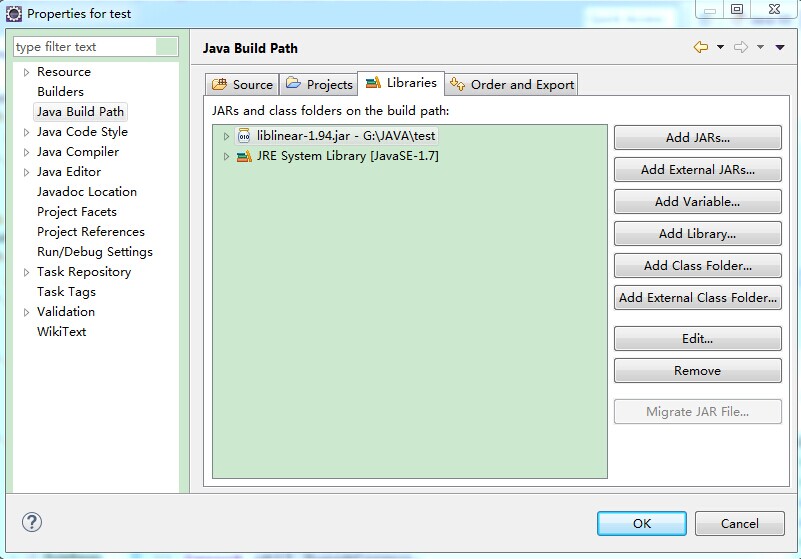
在工程上右键---->Properties----->选中Java Build Path----->选中Libraries标签----->点击Add External JARs。

找到需要添加的jar包，确定即可。

2.创建LibLinear类 (类名自选)

代码如下：

 package liblinear;

 import java.io.File;
 import java.io.IOException;
 import java.util.ArrayList;
 import java.util.List;

 import de.bwaldvogel.liblinear.Feature;
 import de.bwaldvogel.liblinear.FeatureNode;
 import de.bwaldvogel.liblinear.Linear;
 import de.bwaldvogel.liblinear.Model;
 import de.bwaldvogel.liblinear.Parameter;
 import de.bwaldvogel.liblinear.Problem;
 import de.bwaldvogel.liblinear.SolverType;

 public class LibLinear{
     public static void main(String[] args) throws Exception {
         //loading train data
         Feature[][] featureMatrix = new Feature[5][];
         Feature[] featureMatrix1 = { new FeatureNode(2, 0.1), new FeatureNode(3, 0.2) };
         Feature[] featureMatrix2 = { new FeatureNode(2, 0.1), new FeatureNode(3, 0.3), new FeatureNode(4, -1.2)};
         Feature[] featureMatrix3 = { new FeatureNode(1, 0.4) };
         Feature[] featureMatrix4 = { new FeatureNode(2, 0.1), new FeatureNode(4, 1.4), new FeatureNode(5, 0.5) };
         Feature[] featureMatrix5 = { new FeatureNode(1, -0.1), new FeatureNode(2, -0.2), new FeatureNode(3, 0.1), new FeatureNode(4, -1.1), new FeatureNode(5, 0.1) };
         featureMatrix[0] = featureMatrix1;
         featureMatrix[1] = featureMatrix2;
         featureMatrix[2] = featureMatrix3;
         featureMatrix[3] = featureMatrix4;
         featureMatrix[4] = featureMatrix5;
         //loading target value
         double[] targetValue = {1,-1,1,-1,0};

         Problem problem = new Problem();
         problem.l = 5; // number of training examples：训练样本数
         problem.n = 5; // number of features：特征维数
         problem.x = featureMatrix; // feature nodes：特征数据
         problem.y = targetValue; // target values：类别

         SolverType solver = SolverType.L2R_LR; // -s 0
         double C = 1.0;    // cost of constraints violation
         double eps = 0.01; // stopping criteria

         Parameter parameter = new Parameter(solver, C, eps);
         Model model = Linear.train(problem, parameter);
         File modelFile = new File("model");
         model.save(modelFile);
         // load model or use it directly
         model = Model.load(modelFile);

         Feature[] testNode = { new FeatureNode(1, 0.4), new FeatureNode(3, 0.3) };//test node
         double prediction = Linear.predict(model, testNode);
         System.out.print("classification result: "+prediction);
     }
 }

运行后得到testNode的分类结果：

3.参数说明

1. SolverType是solver的类型，可以是如下一种：

分类器：

• L2R_LR：L2-regularized logistic regression (primal)
• L2R_L2LOSS_SVC_DUAL：L2-regularized L2-loss support vector classification (dual)
• L2R_L2LOSS_SVC：L2-regularized L2-loss support vector classification (primal)
• L2R_L1LOSS_SVC_DUAL：L2-regularized L1-loss support vector classification (dual)
• MCSVM_CS：supportvector classification by Crammer and Singer
• L1R_L2LOSS_SVC：L1-regularized L2-loss support vector classification
• L1R_LR：L1-regularized logistic regression
• L2R_LR_DUAL：L2-regularized logistic regression (dual)

回归模型：

• L2R_L2LOSS_SVR：L2-regularized L2-loss support vector regression (primal)
• L2R_L2LOSS_SVR_DUAL：L2-regularized L2-loss support vector regression (dual)
• L2R_L1LOSS_SVR_DUAL：L2-regularized L1-loss support vector regression (dual)

2. C 是约束violation的代价参数 （默认为1）

3. eps 是迭代停止条件的容忍度tolerance

本程序采用的训练样本如下（5个训练样本，5维特征）：

label	feature1	feature2	feature3	feature4	feature5
1	0	0.1	0.2	0	0
-1	0	0.1	0.3	-1.2	0
1	0.4	0	0	0	0
-1	0	0.1	0	1.4	0.5
0	-0.1	-0.2	0.1	1.1	0.1

测试样本为testNode变量：（0.4,0,0.3,0,0）

---

本文为原创博客，若转载请注明出处。