Unique Binary Search Trees leetcode java

题目：

Given n, how many structurally unique BST's (binary search trees) that store values 1...n?

For example,
Given n = 3, there are a total of 5 unique BST's.

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

题解：
 这道题我自己是没啥思路的，感觉就是一种排列组合的计算，但是又不太会。。然后网上查了一下，说要用卡特兰数。。
我下面的带引号的讲解引用Code Ganker(http://blog.csdn.net/linhuanmars/article/details/24761459)的了：
“这道题要求可行的二叉查找树的数量，其实二叉查找树可以任意取根，只要满足中序遍历有序的要求就可以。从处理子问题的角度来看，选取一个结点为根，就把结点
切成左右子树，以这个结点为根的可行二叉树数量就是左右子树可行二叉树数量的乘积，所以总的数量是将以所有结点为根的可行结果累加起来。写成表达式如下：

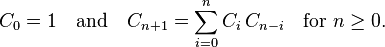
熟悉卡特兰数的朋友可能已经发现了，这正是卡特兰数的一种定义方式，是一个典型的动态规划的定义方式（根据其实条件和递推式求解结果）。所以思路也很明确了，维护量res[i]表示含有i个结点的二叉查找树的数量。根据上述递推式依次求出1到n的的结果即可。

时间上每次求解i个结点的二叉查找树数量的需要一个i步的循环，总体要求n次，所以总时间复杂度是O(1+2+...+n)=O(n^2)。空间上需要一个数组来维护，并且需要前i个的所有信息，所以是O(n)。"

看到了一个解释的更清楚的分析，转自http://fisherlei.blogspot.com/2013/03/leetcode-unique-binary-search-trees.html：

“

这题想了好久才想清楚。其实如果把上例的顺序改一下，就可以看出规律了。

      1         3     3      2      1
       \       /     /      / \      \
        3     2     1      1   3      2
       /     /       \                 \
      2     1         2                 3

比如，以1为根的树有几个，完全取决于有二个元素的子树有几种。同理，2为根的子树取决于一个元素的子树有几个。以3为根的情况，则与1相同。

定义Count[i] 为以[0,i]能产生的Unique Binary Tree的数目，

如果数组为空，毫无疑问，只有一种BST，即空树，
   
Count[0] =1

如果数组仅有一个元素{1}，只有一种BST，单个节点
   
Count[1] = 1

如果数组有两个元素{1,2}， 那么有如下两种可能
   
1                       2
     \                    /
       2                1
   
Count[2] = Count[0] * Count[1]   (1为根的情况)
                  + Count[1] * Count[0]  (2为根的情况。

再看一遍三个元素的数组，可以发现BST的取值方式如下：
   
Count[3] = Count[0]*Count[2]  (1为根的情况)
                  + Count[1]*Count[1]  (2为根的情况)
                  + Count[2]*Count[0]  (3为根的情况)

所以，由此观察，可以得出Count的递推公式为
   
Count[i] = ∑ Count[0...k] * [ k+1....i]     0<=k<i-1
   
问题至此划归为一维动态规划。

[Note]
   
这是很有意思的一个题。刚拿到这题的时候，完全不知道从那下手，因为对于BST是否Unique，很难判断。最后引入了一个条件以后，立即就清晰了，即
   
当数组为 1，2，3，4，.. i，.. n时，基于以下原则的BST建树具有唯一性：
  
以i为根节点的树，其左子树由[1, i-1]构成， 其右子树由[i+1, n]构成。

”

同时为了根据递推式来写程序，需要将递推式简化一下。

根据卡特兰数，C0Cn+1，因为leetcode输入的参数是n，所以为了避免混淆，这里递推式写成Ct+1,初始值为C0 = 1。

原始的递推式是： Ct+1 += Ci*Ct-i (0<= i <=t)

现在令变量num=t+1，那么t=num-1

所以原始递推式做变量替换得：Cnum += Ci*Cnum-1-i (0<= i <=num-1)

而num的取值范围是[1, n]因为C0已知。

代码如下：

 1     public int numTrees(int n) {
 2         if(n == 0||n == 1)
 3             return 1;
 4         
 5         int[] C = new int[n+1];
 6         C[0] = 1;
 7      //递推式是Ct+1 += Ci*Ct-i(0<= i <= t)
 8      //令num = t+1
 9      //则 t = num-1;
      //因此递推式化为：
      //Cnum += Ci*Cnum-1-i(0<=i<=num-1, 1<=num<=n)
      //C0 = 1
 
     for(int num=1;num<=n;num++){  
         for(int i=0;i<=num-1;i++){  
             C[num] += C[i]*C[(num-1)-i];  
         }  
     }
         return C[n];
     }