51nod 1463 找朋友（线段树+离线处理）

http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1463

题意：

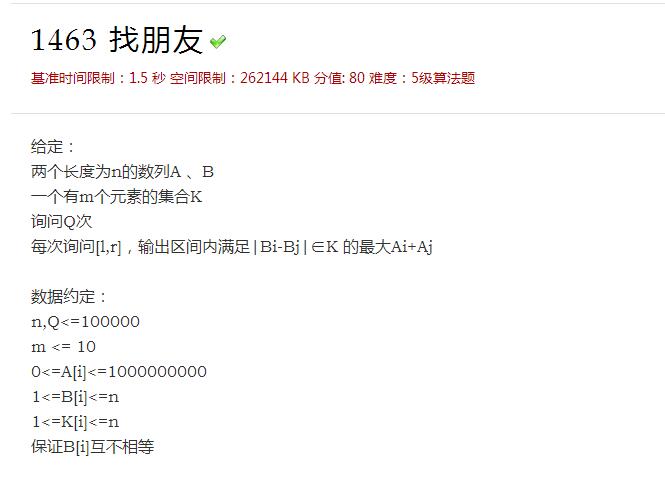
思路：

好题！

先对所有查询进行离线处理，按照右区间排序，因为k一共最多只有10个，所有在该区间内的B数组，每次枚举K值，通过这样的方式来得到另外一个B值。但是这样得到的B值它在B数组中的位置必须在当前数的左边。如下图：（j为当前数在B数组中的位置，pos为计算得到的另一个B值在数组中的位置）

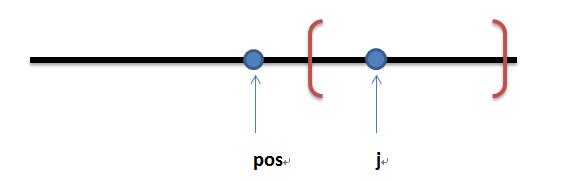
这两个数的和记录在pos中，这里pos的位置必须在j的左边，假设第q个查询区间如上图所示（请在脑中将pos和j互换一下），那么此时j就没包含在该区间内，这样一来，查询得到的值就会有错。因为我们是按照右区间排序的，所以右区间会不断扩大，只要左边被覆盖的，那么右边的数肯定是在该区间内的。

用线段树维护即可。具体请参见代码。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 const int INF = 0x3f3f3f3f;
 const int maxn=1e5+;

 int n,q,m;
 int A[maxn],B[maxn],K[],B_pos[maxn],ans[maxn];

 struct node
 {
     int l,r,id;
     bool operator<(const node& rhs) const
     {
         return r<rhs.r;
     }
 }Q[maxn];

 int MAX[maxn<<];
 int val[maxn<<];

 void build(int l, int r, int o)
 {
     val[o]=;
     if(l==r)  return;
     int mid=(l+r)>>;
     build(l,mid,o<<);
     build(mid+,r,o<<|);
 }

 void update(int l, int r, int pos, int x, int o)
 {
     val[o]=max(val[o],x);
     if(l==pos && r==pos)  return;
     int mid=(l+r)>>;
     if(pos<=mid)  update(l,mid,pos,x,o<<);
     else   update(mid+,r,pos,x,o<<|);
 }

 int query(int ql, int qr, int l, int r, int o)
 {
     if(ql<=l && qr>=r)  return val[o];
     int mid=(l+r)>>;
     int res=;
     if(ql<=mid)  res=max(res,query(ql,qr,l,mid,o<<));
     if(qr>mid)   res=max(res,query(ql,qr,mid+,r,o<<|));
     return res;
 }

 int main()
 {
    //freopen("in.txt","r",stdin);
     scanf("%d%d%d",&n,&q,&m);
     for(int i=;i<=n;i++)  scanf("%d",&A[i]);
     for(int i=;i<=n;i++)  {scanf("%d",&B[i]);B_pos[B[i]]=i;}
     for(int i=;i<=m;i++)  scanf("%d",&K[i]);
     for(int i=;i<=q;i++)
     {
         scanf("%d%d",&Q[i].l,&Q[i].r);
         Q[i].id=i;
     }
     sort(Q+,Q+q+);
     build(,n,);
     int s=;
     memset(MAX,,sizeof(MAX));
     for(int i=;i<=q;i++)
     {
         int r=Q[i].r;
         for(int j=s;j<=r;j++)
         {
             for(int k=;k<=m;k++)
             {
                 int tmp_B=B[j]+K[k];
                 int pos=B_pos[tmp_B];  //得到tmp_B在B数组中的位置
                 if(tmp_B<=n && pos<j && A[pos]+A[j]>MAX[pos])
                 {
                     MAX[pos]=A[pos]+A[j];  //此时pos位置的最大值是由pos和[1,j)之间的一个数相加而成
                     update(,n,pos,MAX[pos],); //更新线段树
                 }
                 tmp_B=B[j]-K[k];
                 pos=B_pos[tmp_B];
                 if(tmp_B>= && pos<j && A[pos]+A[j]>MAX[pos])
                 {
                     MAX[pos]=A[pos]+A[j];
                     update(,n,pos,MAX[pos],);
                 }
             }
         }
         ans[Q[i].id]=query(Q[i].l,Q[i].r,,n,); //查询该区间内的最大值
         s=r;
     }
     for(int i=;i<=q;i++)  printf("%d\n",ans[i]);
     return ;
 }

再给一个树状数组的吧，按照左区间从大到小排序。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 const int INF = 0x3f3f3f3f;
 const int maxn=1e5+;

 int n,q,m;
 int A[maxn],B[maxn],K[],B_pos[maxn],ans[maxn],c[maxn];

 struct node
 {
     int l,r,id;
     bool operator<(const node& rhs) const
     {
         return l>rhs.l;
     }
 }Q[maxn];

 int lowbit(int x)
 {
     return x&(-x);
 }

 int find_max(int x)
 {
     int res=;
     while(x>)
     {
         res=max(res,c[x]);
         x-=lowbit(x);
     }
     return res;
 }

 void update(int x, int val)
 {
     while(x<=n)
     {
         c[x]=max(c[x],val);
         x+=lowbit(x);
     }
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     scanf("%d%d%d",&n,&q,&m);
     for(int i=;i<=n;i++)  scanf("%d",&A[i]);
     for(int i=;i<=n;i++)  {scanf("%d",&B[i]);B_pos[B[i]]=i;}
     for(int i=;i<=m;i++)  scanf("%d",&K[i]);
     for(int i=;i<=q;i++)
     {
         scanf("%d%d",&Q[i].l,&Q[i].r);
         Q[i].id=i;
     }
     sort(Q+,Q+q+);
     memset(c,,sizeof(c));
     int s=n+;
     for(int i=;i<=q;i++)
     {
         for(int j=s-;j>=Q[i].l;j--)
         {
             for(int k=;k<=m;k++)
             {
                 int tmp_B=B[j]+K[k];
                 int pos=B_pos[tmp_B];
                 if(tmp_B<=n && pos>j)
                 {
                     update(pos,A[pos]+A[j]);
                 }
                 tmp_B=B[j]-K[k];
                 pos=B_pos[tmp_B];
                 if(tmp_B>= && pos>j)
                 {
                     update(pos,A[pos]+A[j]);
                 }
             }
         }
         s=Q[i].l;
         ans[Q[i].id]=find_max(Q[i].r);
     }

     for(int i=;i<=q;i++)  printf("%d\n",ans[i]);
     return ;
 }