『科学计算』可视化二元正态分布&3D科学可视化实战

二元正态分布可视化本体

由于近来一直再看kaggle的入门书（sklearn入门手册的感觉233），感觉对机器学习的理解加深了不少（实际上就只是调包能力加强了），联想到假期在python科学计算上也算是进行了一些尝试学习，觉得还是需要学习一下机器学习原理的，所以重新啃起了吴恩达的cs229，上次（5月份的时候？）就是在多元高斯分布这里吃的瘪，看不下去了，这次觉定稳扎稳打，不求速度多实践实践，尽量理解数学原理，所以再次看到这部分时决定把这个分布复现出来，吴恩达大佬用的matlab，我用的python，画的还不错，代码如下，

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
import matplotlib as mpl

num = 200
l = np.linspace(-5,5,num)
X, Y =np.meshgrid(l, l)

u = np.array([0, 0])
o = np.array([[1, 0.5],
              [0.5, 1]])

pos = np.concatenate((np.expand_dims(X,axis=2),np.expand_dims(Y,axis=2)),axis=2)

a = (pos-u).dot(np.linalg.inv(o))
b = np.expand_dims(pos-u,axis=3)
Z = np.zeros((num,num), dtype=np.float32)
for i in range(num):
    Z[i] = [np.dot(a[i,j],b[i,j]) for j in range(num)]
Z = np.exp(Z*(-0.5))/(2*np.pi*np.linalg.det(o))
fig = plt.figure()
ax = fig.add_subplot(111,projection='3d')
ax.plot_surface(X, Y, Z, rstride=5, cstride=5, alpha=0.3, cmap=cm.coolwarm)

cset = ax.contour(X,Y,Z,10,zdir='z',offset=0,cmap=cm.coolwarm)
cset = ax.contour(X, Y, Z, zdir='x', offset=-5,cmap=mpl.cm.winter)
cset = ax.contour(X, Y, Z, zdir='y', offset= 5,cmap= mpl.cm.winter)
'''
mpl.cm.rainbow
mpl.cm.winter
mpl.cm.bwr  # 蓝，白，红
cm.coolwarm
'''

ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()　

实际操作中，可以看到我在Z生成部分使用了双层循环，我本意是使用numpy广播机制优化掉循环，实际操作不太顺利，（20，20，2）去叉乘（20，20，2，1），结果shape不是我期望的（20，20，1），而是（20，20，20，20，1），也就是说在高维叉乘时其实广播机制不太好用，毕竟实际上两个不同维度矩阵是可以直接叉乘的（虽然对维度有要求），这一点值得注意（高维矩阵叉乘不要依赖numpy的广播机制）。

参数：

u = np.array([0, 0]) 
o = np.array([[1, 0.5], 
             [0.5, 1]])

　

参数：

u = np.array([1, 1])
o = np.array([[1, 0],
              [0, 1]])

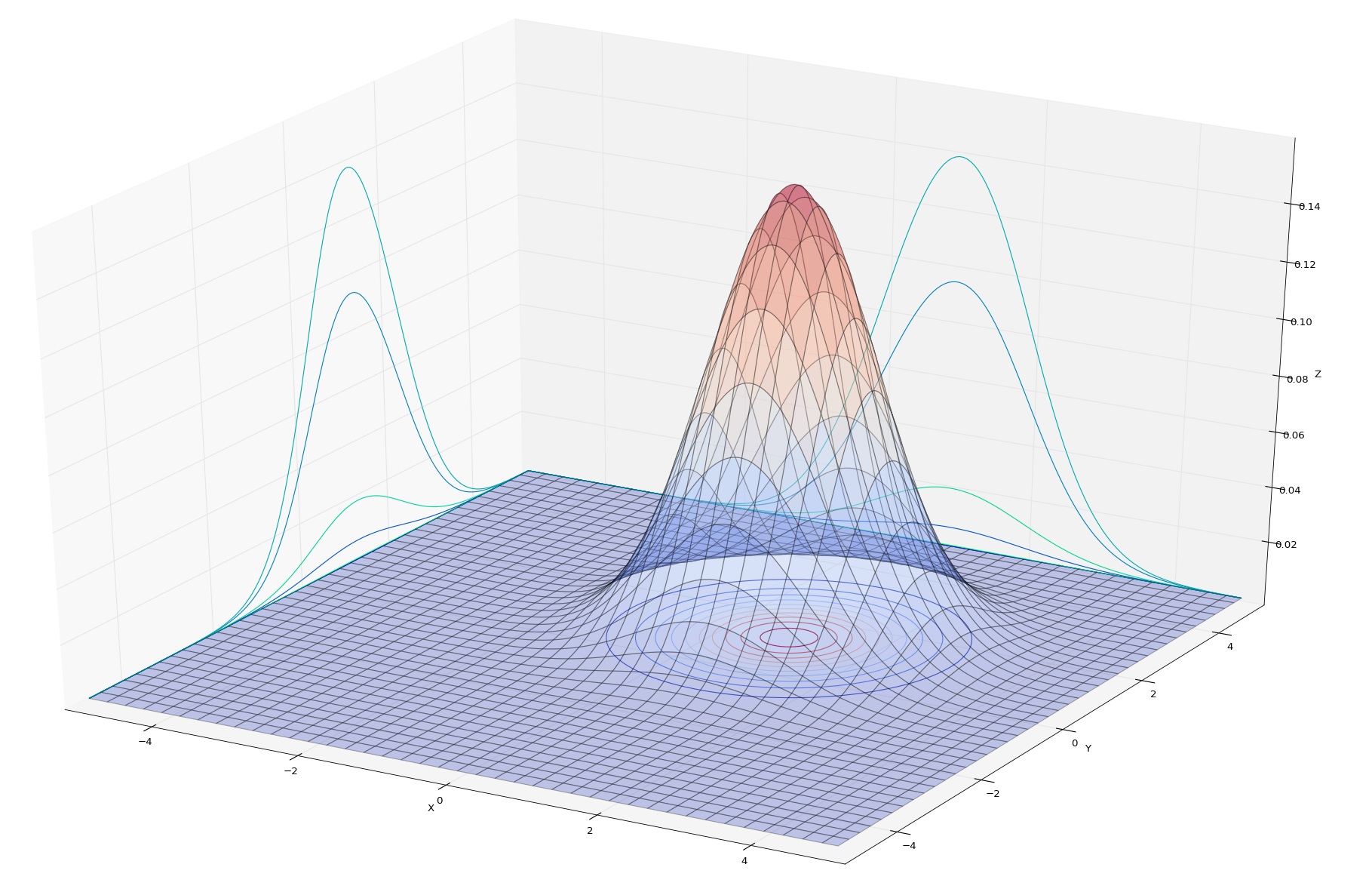
参数：

u = np.array([1, 1])
o = 3*np.array([[1, 0],
              [0, 1]])

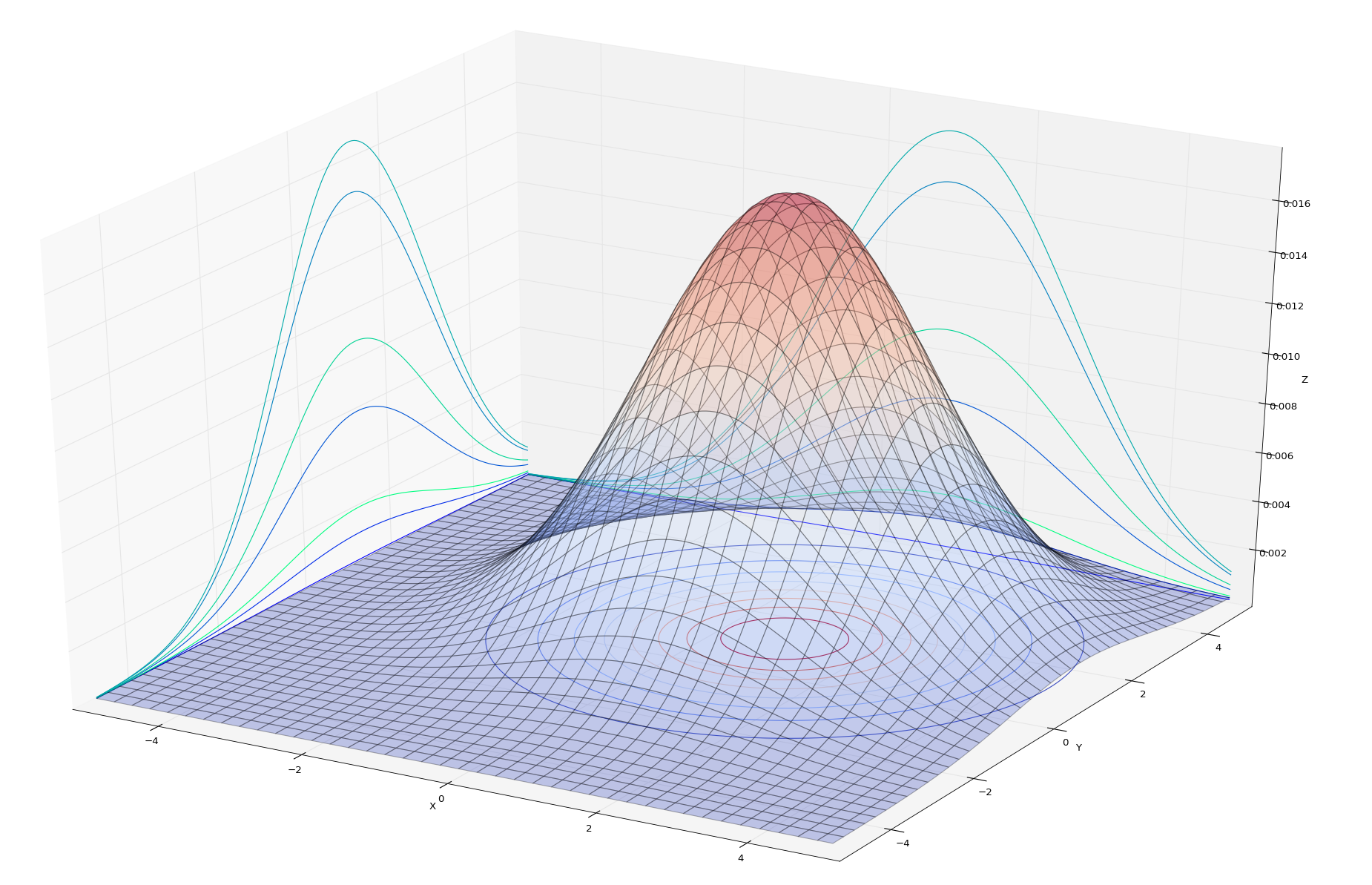
等高线图添加

我们单独绘制一下等高线图，

# 前面添加图的位置修改如下，
# ax = fig.add_subplot(211,projection='3d')

ax2 = fig.add_subplot(212)
cs = ax2.contour(X,Y,Z)
ax2.clabel(cs, inline=1, fontsize=20)

高斯判别分析模型示意图可视化

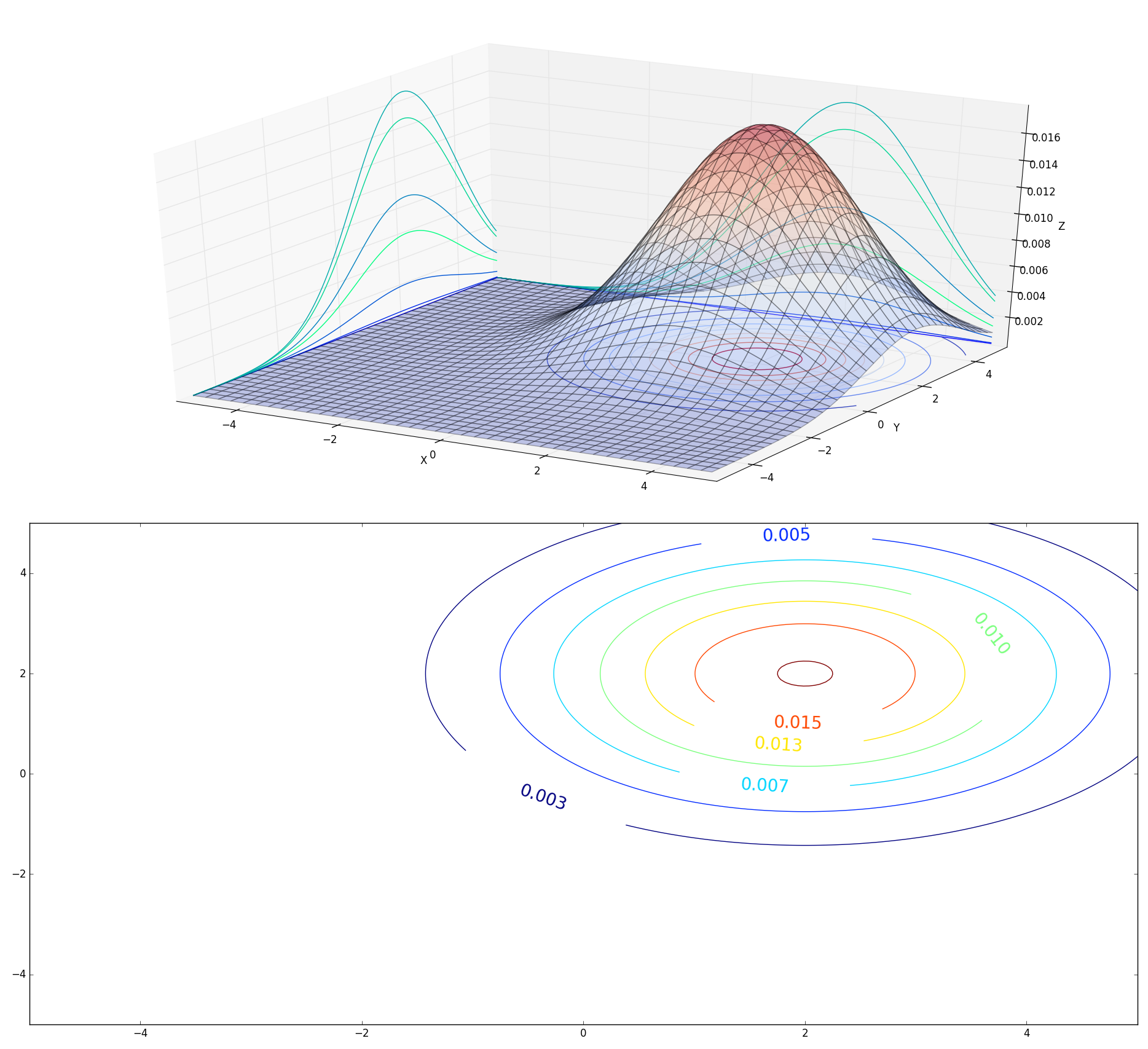
现在我们在上面代码的基础上可视化吴恩达老大的下一节的图，高斯判别分析模型可视化，这里面我们仅仅可视化基础的双高斯独立分布，代码如下，

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
import matplotlib as mpl

num = 200
l = np.linspace(-5,5,num)
X, Y =np.meshgrid(l, l)
pos = np.concatenate((np.expand_dims(X,axis=2),np.expand_dims(Y,axis=2)),axis=2)

u1 = np.array([2, 2])
o1 = 3*np.array([[1, 0],
              [0, 1]])
a1 = (pos-u1).dot(np.linalg.inv(o1))
b1 = np.expand_dims(pos-u1,axis=3)
Z1 = np.zeros((num,num), dtype=np.float32)

u2 = np.array([-2, -2])
o2 = 3*np.array([[1, 0],
              [0, 1]])
a2 = (pos-u2).dot(np.linalg.inv(o2))
b2 = np.expand_dims(pos-u2,axis=3)
Z2 = np.zeros((num,num), dtype=np.float32)

for i in range(num):
    Z1[i] = [np.dot(a1[i,j],b1[i,j]) for j in range(num)]
    Z2[i] = [np.dot(a2[i,j],b2[i,j]) for j in range(num)]
Z1 = np.exp(Z1*(-0.5))/(2*np.pi*np.linalg.det(o1))
Z2 = np.exp(Z2*(-0.5))/(2*np.pi*np.linalg.det(o1))

Z = Z1 + Z2

fig = plt.figure()
ax = fig.add_subplot(211,projection='3d')
ax.plot_surface(X, Y, Z, rstride=5, cstride=5, alpha=0.3, cmap=cm.coolwarm)

cset = ax.contour(X,Y,Z,10,zdir='z',offset=0,cmap=cm.coolwarm)
cset = ax.contour(X, Y, Z, zdir='x', offset=-5,cmap=mpl.cm.winter)
cset = ax.contour(X, Y, Z, zdir='y', offset= 5,cmap= mpl.cm.winter)
'''
mpl.cm.rainbow
mpl.cm.winter
mpl.cm.bwr  # 蓝，白，红
cm.coolwarm
'''

ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

ax2 = fig.add_subplot(212)
cs = ax2.contour(X,Y,Z)
ax2.clabel(cs, inline=1, fontsize=20)

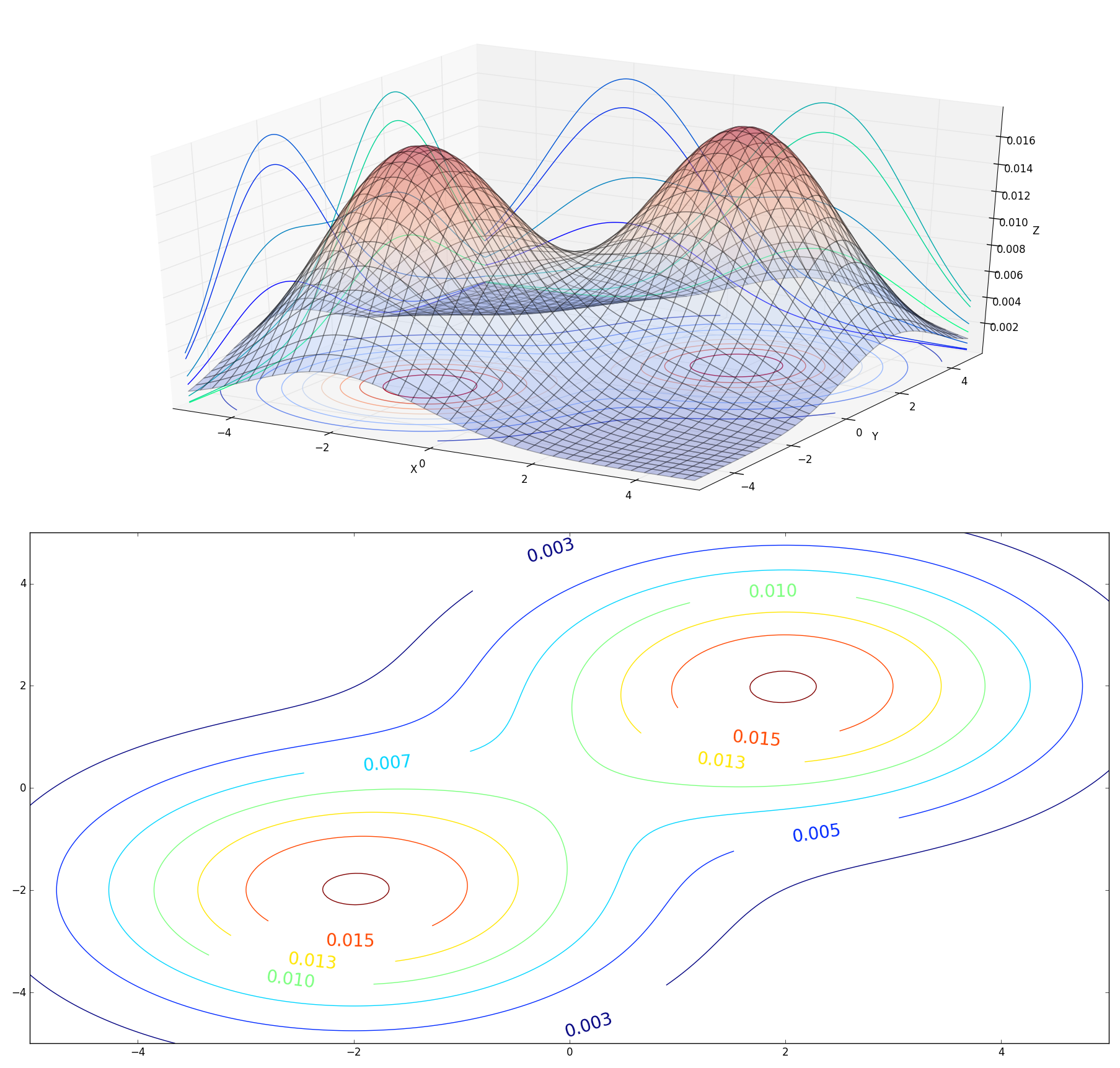
不过吴老大的图两个高斯分布投影是分开的，所以我们再次小改绘图部分，

cset = ax.contour(X,Y,Z1,10,zdir='z',offset=0,cmap=cm.coolwarm)
cset = ax.contour(X,Y,Z2,10,zdir='z',offset=0,cmap=cm.coolwarm)
cset = ax.contour(X, Y, Z, zdir='x', offset=-5,cmap=mpl.cm.winter)
cset = ax.contour(X, Y, Z, zdir='y', offset= 5,cmap= mpl.cm.winter)
'''
mpl.cm.rainbow
mpl.cm.winter
mpl.cm.bwr  # 蓝，白，红
cm.coolwarm
'''

ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

ax2 = fig.add_subplot(212)
cs = ax2.contour(X,Y,Z1)
ax2.clabel(cs, inline=1, fontsize=20)
cs2 = ax2.contour(X,Y,Z2)
ax2.clabel(cs2, inline=1, fontsize=20)

显示如下，框子不够标准导致圆有点变形，不过这个可以通过手动拉伸得到优化，所以问题不大，

有关多元正态分布的数学原理建议自行百度（cs229的学习不会在博客上更新，主要是因为我非常非常讨厌打数学公式233）。