求最长回文子串——Manacher算法

回文串包括奇数长的和偶数长的，一般求的时候都要分情况讨论，这个算法做了个简单的处理把奇偶情况统一了。算法的基本思路是这样的，把原串每个字符中间用一个串中没出现过的字符分隔开来(统一奇偶)，用一个数组p[ i ]记录以 str[ i ] 为中间字符的回文串向右能匹配的长度。先看个例子

原串：       w  a   a   b   w   s   w   f   d

新串(str):  #   w  #   a   #   a   #   b  #   w   #   s    #   w    #     f    #    d     #

0   1   2   3   4    5   6   7   8   9  10  11 12  13  14   15  16   17   18

p数组：     1   2   1   2   3    2   1   2   1   2   1    4   1    2    1     2    1    2    1

由p数组的性质，新串中以str[i]为中间字符的回文串的长度为p[i]-1（可以对照p[11]这个位置，p[i]-1本身表示对称半径，但是实际上去掉#以后，p[i]-1就是回文串长度），以#为中间字符的就是长度为偶数的，以非#号为中间字符的就是长度为奇数的，那么怎么求p[ ]数组呢？

从左到右计算（0~str.length），也就是计算p[i]时，p[0.....i-1] 都已经计算出来了，并且用一个变量mx记录当前检测出的回文串的右侧最大位置 max{ k+p[ k ] } (k=0.....i-1),用id记录取最大值时的k。

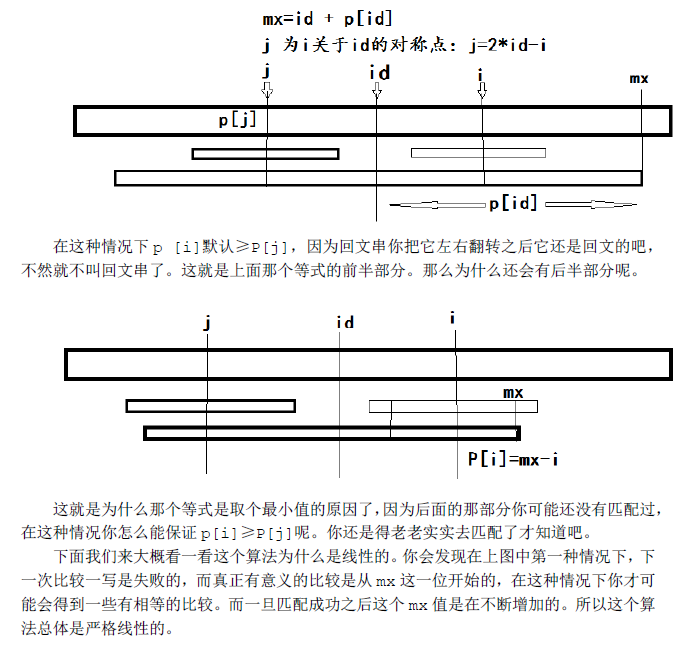
上面的这个截图是很多人都用过的，需要注意的是， 两张图分别表示了当前点i<mx时的两种情况：

1) 当前点i关于id的对称点j, 以j为中心的回文串的左边界不小于id-p[id]，根据回文串的对称性， 这就意味着i的回文串长度是跟j是一样的， 所以有p[i] = p[j] = p[2*id-i];

2) 如果以j为中心的回文串的左边界小于id-p[id]，则只能确保p[i]>=mx-i, 至于p[i]的值具体为多少，还需要检测mx后面的位置才能确定出来。

所以就有了下面的这个关键代码，理解了这部分，整个算法就好理解了。

if( mx > i )

p[i] = MIN( p[*id-i], mx-i );

完整代码如下：

 #include<iostream>
 #include<string>
 #include<stdlib.h>
 using namespace std;

 char cArray[];
 int p[];

 int manacher(int length)
 {
     int mx = ;
     int id = ;
     int maxLength = ;

     for(int i=; i<length; ++i)
     {
         if(mx>i)
         {
             p[i] = min(p[*id-i], mx-i);
         }
         else
         {
             p[i] = ;
         }

         while( (i-p[i]+)>= && (i+p[i]-)<length && cArray[i-p[i]+]==cArray[i+p[i]-] )
         {
             p[i] = p[i] + ;
         }

         p[i]--;

         if(i+p[i]- > mx)
         {
             mx = i+p[i]-;
             id = i;
         }

         if(maxLength < p[i]-)
         {
             maxLength = p[i]-;
         }
     }

     return maxLength;
 }

 int main()
 {
     //string input = "waabwswfd";
     string input = "wawbbbwasaw";
     int k = ;
     for(int i=; i<input.size(); ++i)
     {
         cArray[k++] = '#';
         cArray[k++] = input.at(i);
     }
     cArray[k++] = '#';
     int ans = manacher(k);
     cout << ans << endl;
 }

简化以后的代码

#include<iostream>
#include<string>
#include<cstdlib>
#include<algorithm>

using namespace std;

char cArray[];
int p[];

int manacher(int length)
{
    int mx = ;
    int id = ;
    int maxLength = ;

    for (int i = ; i<length; ++i)
    {
        if (mx>i)
        {
            p[i] = min(p[ * id - i], mx - i);
        }
        else
        {
            p[i] = ;
        }

        while ((i - p[i]) >=  && (i + p[i])<length && cArray[i - p[i]] == cArray[i + p[i]])
        {
            p[i] = p[i] + ;
        }

        p[i]--;

        if (i + p[i] > mx)
        {
            mx = i + p[i];
            id = i;
        }

        if (maxLength < p[i])
        {
            maxLength = p[i];
        }
    }

    return maxLength;
}

int main()
{
    //string input = "waabwswfd";
    string input = "wawbbbwasaw";
    int k = ;
    for (int i = ; i<input.size(); ++i)
    {
        cArray[k++] = '#';
        cArray[k++] = input.at(i);
    }
    cArray[k++] = '#';
    int ans = manacher(k);
    cout << ans << endl;
}