cf(#div1 A. Dreamoon and Sums)(数论)

A. Dreamoon and Sums

time limit per test

1.5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Dreamoon loves summing up something for no reason. One day he obtains two integers a and b occasionally. He wants to calculate the sum of all nice integers. Positive integer x is called nice if 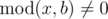and 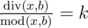, where k is some integer number in range [1, a].

By 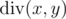we denote the quotient of integer division of x and y. By 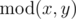we denote the remainder of integer division of x and y. You can read more about these operations here: http://goo.gl/AcsXhT.

The answer may be large, so please print its remainder modulo 1 000 000 007 (10⁹ + 7). Can you compute it faster than Dreamoon?

Input

The single line of the input contains two integers a, b (1 ≤ a, b ≤ 10⁷).

Output

Print a single integer representing the answer modulo 1 000 000 007 (10⁹ + 7).

Sample test(s)

Input

1 1

Output

0

Input

2 2

Output

8

Note

For the first sample, there are no nice integers because 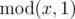is always zero.

For the second sample, the set of nice integers is {3, 5}.

题意：

给你两个整数a,b ,定义这样一个数为漂亮数：

(1) x>0  ;  (2)x%b!=0 ;  (3)  (x/b)/(x%b)=k;  (4)k属于[1,a];

求这样的漂亮数的所有之和。

对于这样题，分析起来其实还是很简单的， 对于求和（sum），我们需要做的第一件事就是确定漂亮数的边界（上限和下限）、由于（3） (x/b)/(x%b)=k

可以得出： x/b = k*(x%b);              x%b的剩余系即{1，2,3,4,5，......b-1}里的最大系;我们不放设定y={1,2,3,4,5,........b-1};

不难得出：  x=k*y*b+y; -->x=(k*b+1)*y 所以可以推断公式：  x=Σ₁^a (k*b+1)*Σ₁^b-1 (y);

进一步简化后部分： x=Σ₁^a (k*b+1)*（b-1）*(b)/2;

所以代码为：

 #include<cstdio>
 #include<cstring>
 #define LL __int64
 #define mod 1000000007
 int main()
 {
   LL  a,b;
   LL sum;
   while(scanf("%I64d%I64d",&a,&b)!=EOF)
   {
         sum=;
       for(LL j=;j<=a;j++)
       {
           sum+=((j*b)%mod+)%mod;
           sum%=mod;
       }
       LL ans=(((b-)*b)/)%mod;
      printf("%I64d\n",(sum*ans)%mod);
   }
   return ;
 }