poj2528(线段树+离散化)Mayor's posters

2016-08-15

题意：一面墙，往上面贴海报，后面贴的可以覆盖前面贴的。问最后能看见几种海报。

思路：可以理解成往墙上涂颜色，最后能看见几种颜色（下面就是以涂色来讲的）。这面墙长度为1~1000 0000，一千万，确实很大。暴力的话肯定不行，除非..（ you know）。

正确的解法是用线段树，不过还得加上离散化，因为数据太大10000000啊。

先说一下离散化，这个其实就是压缩，把范围压缩，举个例子:

输入 ：

1 3000    //涂第一种颜色 范围从1~10000      下面同理

2000 7000  //第二种颜色

我们可以先把输入的数据范围压缩，假如输入的数据存到数组a[0]=1,a[1]=3000,a[2]=2000,a[3]=7000。

离散化（压缩）过程：

先把a[]从小到大排序。然后接着

把a数组里的数据映射到dis数组里，这样涂颜色（插入）的时候用dis[a[i]]。

压缩完之后建树的时候只需建1~4范围的树，而不用建1~7000的树。所以说离散化是必须的...懂嘞谬？

离散化完事后，再说说线段树，到底是个什么树呢？

比如1~10这个线段，用二叉树的形式储存起来，

看图：

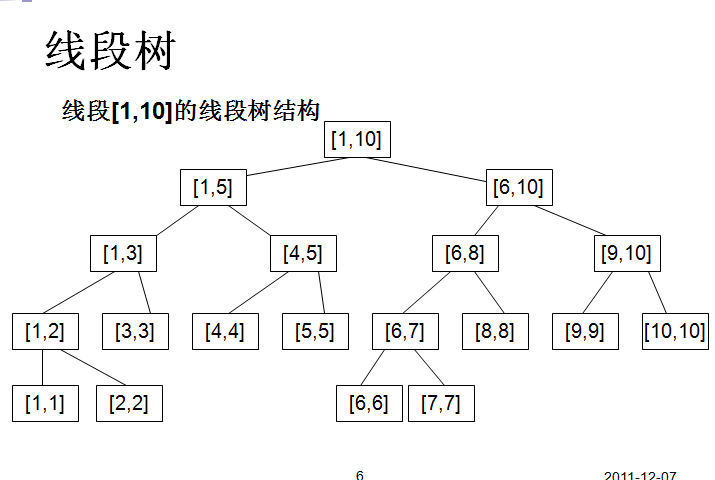
然后在每个节点加上各种信息，就可以用了，虽然空间大了但时间快了

对于这个问题 线段树主要用了三个函数

void build(int p,int a,int b) //建树

void update(int p,int col,int a,int b)//插入颜色

void query(int p)  //查询颜色

代码有详细解释

AC代码：

 #include <iostream>
 #include <cstring>
 #include <cstdio>
 #include <algorithm>
 using namespace std;

 const int MAXN=;

 bool tagcol[MAXN];   //标记颜色是否已经计算过

 int e[MAXN<<];     //临时数组，把重复的数据去掉
 int ee[MAXN][];    //直接输入数据的数组 存每张海报的范围的
 int dis[];   //离散化之后的映射数组
 int cnt=;           //颜色计数器

 struct node     //线段树节点
 {
     int l,r;    //l~r 范围
     int c;    //颜色（用1,2,3...表示）
 }LTnode[MAXN<<];    //开数组的时候尽量开大点，开8倍就Runtime Error了，开16倍就过，虽然不知道为啥

 void build(int p,int a,int b)   //建树，p是节点下标，范围 a~b
 {
     LTnode[p].l=a;
     LTnode[p].r=b;
     LTnode[p].c=;
     if(a==b)    //到叶子节点直接返回
     {
         return;
     }

     //继续递归建树
     int mid=(a+b)>>;
     build(p<<,a,mid);
     build(p<<|,mid+,b);
     return;
 }
 void update(int p,int col,int a,int b)   //更新（插入）颜色，p是节点下标，col是颜色，a,b是要更新的范围
 {
     if(LTnode[p].l>=a&&LTnode[p].r<=b)   //如果当前节点范围 正好在a,b内，更新颜色 返回
     {
         LTnode[p].c=col;
         return;
     }
     if(LTnode[p].r<a||LTnode[p].l>b)   //如果当前节点范围和a,b没有交集
         return;
     if(LTnode[p].c>=)   //当前节点和a,b有部分交集
     {
         LTnode[p<<].c=LTnode[p<<|].c=LTnode[p].c;  //把当前节点的颜色传递给左右孩子节点，灰常重要
         LTnode[p].c=-;    //-1代表有多种颜色
     }
     //继续处理左右孩子
     update(p<<,col,a,b);
     update(p<<|,col,a,b);
     return;
 }

 void query(int p)   //查询,p是节点下标
 {
     if(LTnode[p].c==)  //当前节点的颜色为0，即没有颜色
         return;
     if(LTnode[p].c>&&!tagcol[LTnode[p].c])  //当前节点有某种颜色并且该颜色没有被计算过
     {
         cnt++;  //颜色计数器+1
         tagcol[LTnode[p].c]=true;
         return;
     }
     if(LTnode[p].c==-)  //多色 则继续细化处理左右孩子
     {
         query(p<<);
         query(p<<|);
     }
     return;

 }

 int main()
 {
     int T;
     scanf("%d",&T);
     while(T--)
     {

         memset(tagcol,false,sizeof(tagcol));
         memset(dis,,sizeof(dis));

         int n;   //n表示有几张海报
         //cin>>n;
         scanf("%d",&n);
         int maxp=;
         for(int i=;i<n;i++)
         {
             //cin>>ee[i][0]>>ee[i][1];
             scanf("%d%d",&ee[i][],&ee[i][]);  //poj上用scanf就过，cin就TLE 坑啊...
             if(!dis[ee[i][]])   //用dis数组先标记下 有没有重复的数据 这样就不用再开一个数组了
             {
                 e[maxp++]=ee[i][];
                 dis[ee[i][]]=;
             }
             if(!dis[ee[i][]])
             {
                 e[maxp++]=ee[i][];
                 dis[ee[i][]]=;
             }
         }
         memset(dis,,sizeof(dis));
         int has=;
         sort(e,e+maxp);   //先排序
         for(int i=;i<maxp;i++)  //for循环出来后 has 就是离散后的最大范围
         {
             dis[e[i]]=++has;
         }
         build(,,has);
         for(int i=;i<n;i++)   //一次插入颜色，i为颜色
         {
             update(,i+,dis[ee[i][]],dis[ee[i][]]);
         }
         cnt=;
         query();
         cout<<cnt<<endl;

     }

     return ;
 }

手打真累啊，肩膀疼..