MT【130】Heilbronn问题

(清华THUSSAT，多选题)
平面上 4 个不同点 \(P_1,P_2,P_3,P_4\)，在每两个点之间连接线段得到 6 条线段. 记
\[L=\max_{1\leq i<j\leq 4}|P_iP_j|,\ l=\min_{1\leq i<j\leq 4}|P_iP_j|,\]
对任意三点不共线的所有四点组 \(P_1,P_2,P_3,P_4\)，把 \(\dfrac{L}{l}\) 的取值集合记为 \(P\)，则
A.\(0.5 \in P\)
B.\(1 \in P\)
C.\(\sqrt{2} \in P\)
D.\(2 \in P\)

答案:C.D，构造如下:

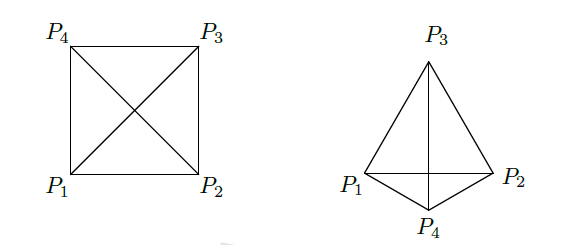
此题是著名的"Heilbronn问题"在4个点时的情形,一般的由以下结论\(\lambda_n\ge2cos\dfrac{\pi}{n}\)当\(n\ge6\)时尚不知道能否取到等号.
事实上1985全国联赛最后一题就是考察了5个点的情形.

（1985联赛加试）平面上任给5个点，以\(\lambda\)表示这些点间最大的距离与最小的距离之比，证明：\(\lambda≥2sin54^o\)
证明：
⑴ 若此五点中有三点共线，例如A、B、C三点共线，不妨设B在A、C之间，则AB与BC必有一较大者．不妨设AB≥BC．则\(\dfrac{AC}{BC}≥2>2sin54^o\)

⑵ 设此五点中无三点共线的情况．
① 若此五点的凸包为正五边形．则其五个内角都\(=108^o\)五点的连线只有两种长度：正五边形的边长与对角线，而此对角线与边长之比为\(2sin54^o\)．
② 若此五点的凸包为凸五边形．则其五个内角中至少有一个内角\(≥108^o\)．设\(\angle EAB≥108^o\)，且\(EA≥AB\)，则\(\angle AEB≤36^o,\therefore \dfrac{BE}{AB} = \dfrac{sin(B+E)}{sinE} ≥\dfrac{sin2E}{sinE} =2cosE≥2cos36^o=2sin54^o\)．
③ 若此五点的凸包为凸四边形ABCD，点E在其内部，连AC，设点E在\(\Delta ABC\)内部，则\(\angle AEB,\angle BEC,\angle CEA\)中至少有一个角\(≥120^o>108^o\)，由上证可知，结论成立．
④ 若此五点的凸包为三角形ABC，则形内有两点D、E，则\(\angle ADB,\angle BDC,\angle CDA\)中必有一个角\(≥120^o\)，结论成立．
综上可知，结论成立．