The Best Path HDU - 5883（欧拉回路 && 欧拉路径）

The Best Path

Time Limit: 9000/3000 MS (Java/Others)    Memory Limit: 65535/32768 K (Java/Others)
Total Submission(s): 2401    Accepted Submission(s): 945

Problem Description

Alice is planning her travel route in a beautiful valley. In this valley, there are N lakes, and M rivers linking these lakes. Alice wants to start her trip from one lake, and enjoys the landscape by boat. That means she need to set up a path which go through every river exactly once. In addition, Alice has a specific number (a1,a2,...,an) for each lake. If the path she finds is P0→P1→...→Pt, the lucky number of this trip would be aP0XORaP1XOR...XORaPt. She want to make this number as large as possible. Can you help her?

 

Input

The first line of input contains an integer t, the number of test cases. t test cases follow.

For each test case, in the first line there are two positive integers N (N≤100000) and M (M≤500000), as described above. The i-th line of the next Nlines contains an integer ai(∀i,0≤ai≤10000) representing the number of the i-th lake.

The i-th line of the next M lines contains two integers ui and vi representing the i-th river between the ui-th lake and vi-th lake. It is possible that ui=vi.

 

Output

For each test cases, output the largest lucky number. If it dose not have any path, output "Impossible".

 

Sample Input

2
3 2
3
4
5
1 2
2 3
4 3
1
2
3
4
1 2
2 3
2 4

 

Sample Output

2
Impossible

 

就是给出点和路 并且每个点上都有一个权值  要求走过所有的路 使得最后权值的异或和最大

 

题解：

　　走过每一条路 明显为欧拉路问题

　　欧拉路分为两种 1、欧拉回路 2、欧拉路径 

　　即源点和汇点相同  和  源点和汇点不同

　　在输入的时候去统计每一个点的度数 当每个点的度数都为偶数的时候为欧拉回路(一个入度 对应 一个出度)， 当存在两个点的度数为奇数的时候为欧拉路径(源点有奇数个出度  汇点有奇数个入度)

　　其他情况 impossible

　　对于异或 同假异真 所以若某个点经过偶数次 则可以直接不计 只记奇数次的

　　经过某个点的次数 即为 (度数+1)/2  所以遍历每个点的度数 算即可

　　但这样算出来的是 源点和汇点不同的情况的

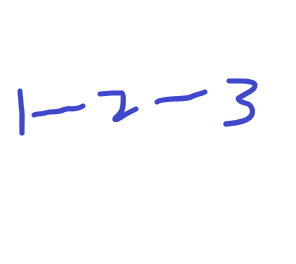　　 如图从1到3 1和3的度数均为1 所以1和3经过(1+1)/2次  2的度数为2 所以为(2+1)/2 次

 

那么源点和汇点相同的怎么算呢

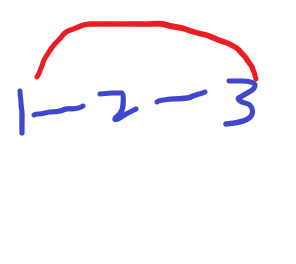  如图 我们设以1为源点 我们只需要枚举源点 再异或一次 即可 如图 虽然1和3之间比上图多了一条边 但是算出来的经过的次数依然和上图的一样1和3是1次  2也是1次  但从1出发最后又回到1了 所以1 经过了两次 所以枚举源点即可

#include <iostream>
#include <cstdio>
#include <sstream>
#include <cstring>
#include <map>
#include <cctype>
#include <set>
#include <vector>
#include <stack>
#include <queue>
#include <algorithm>
#include <cmath>
#define rap(i, a, n) for(int i=a; i<=n; i++)
#define rep(i, a, n) for(int i=a; i<n; i++)
#define lap(i, a, n) for(int i=n; i>=a; i--)
#define lep(i, a, n) for(int i=n; i>a; i--)
#define rd(a) scanf("%d", &a)
#define rlld(a) scanf("%lld", &a)
#define rc(a) scanf("%c", &a)
#define rs(a) scanf("%s", a)
#define MOD 2018
#define LL long long
#define ULL unsigned long long
#define Pair pair<int, int>
#define mem(a, b) memset(a, b, sizeof(a))
#define _  ios_base::sync_with_stdio(0),cin.tie(0)
//freopen("1.txt", "r", stdin);
using namespace std;
const int maxn = , INF = 0x7fffffff;
int w[maxn], drgee[maxn];
int n, m;
int solve()
{
    int cnt = ;
    rap(i, , n)
        if(drgee[i] & )
            cnt++;
    if(cnt !=  && cnt != )
        return -;
    int res = ;
    rap(i, , n)
    {
        drgee[i] = (drgee[i] + ) >> ;
        if(drgee[i] & )
            res ^= w[i];
    }
    int tmp = ;
    if(cnt == )
    {
        rap(i, , n)
        {
            tmp = max(tmp, res^w[i]);
        }
        res = tmp;
    }
    return res;
}

int main()
{
    int T;
    rd(T);
    while(T--)
    {
        mem(drgee, );
        rd(n); rd(m);
        rap(i, , n)
            rd(w[i]);
        rep(i, , m)
        {
            int u, v;
            rd(u); rd(v);
            drgee[u]++;
            drgee[v]++;
        }

        int res = solve();
        if(res == -)
        {
            printf("Impossible\n");
            continue;
        }
        else
        {
            printf("%d\n", res);

        }

    }

    return ;
}