堆 C语言实现

1、基本概念

堆分为小根堆和大根堆，对于一个小根堆，它是具有如下特性的一棵完全二叉树：

（1）若树根结点存在左孩子或右孩子，则根结点的值（或某个域的值）小于等于左右孩子结点的值（或某个域的值）

（2）以左、右孩子为根的子树又各是一个堆。

大根堆的定义将上面的小于等于改成大于等于即可。

根据根的定义，小根堆的堆顶结点具有最小值，大根堆的堆顶结点具有最大值。

2、堆的存储结构

由于堆是一棵完全二叉树，所以适宜采用顺序存储结构，这样能够充分利用存储空间。

顺序存储结构：

对堆中所有结点进行编号，作为下标存储到指定数组的对应元素中，下标从0开始。按照从上到下，同一层从左到右进行。

设堆中有n个结点，则编号为 0 ~ n-1，则有如下性质：

（1）编号为 0 至 [n/2-1] 的结点为分支结点， 编号为 [n/2] 至 n-1 的结点为叶子结点；

（2）当 n 为奇数则每个分支结点既有左孩子又有右孩子，当 n 为偶数则每个分支结点只有左孩子没有右孩子

（3）对于每个编号为 i 的分支结点，其左孩子结点的编号为 2i+1，右孩子结点的编号为 2i+2

（4）除编号为0的堆顶结点外，对于其余编号为 i 的结点，其双亲结点的编号为 [(i-1)/2]

下图为一个堆及其顺序存储结构

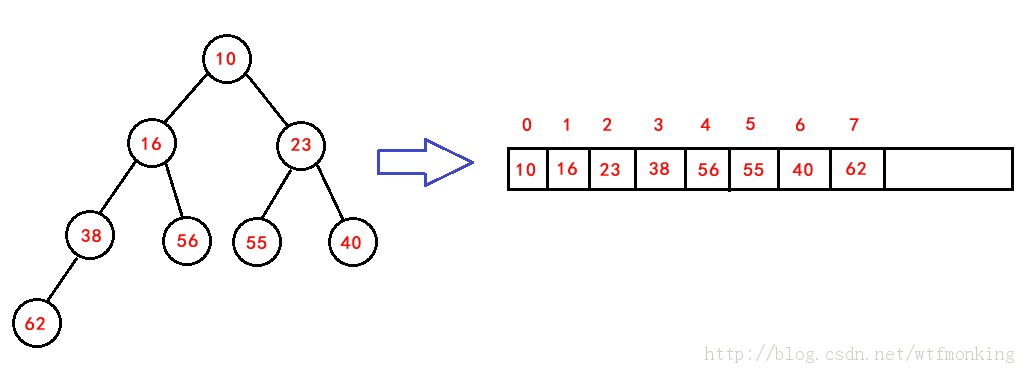
3、堆的操作及运算

用如下程序详细展示堆的操作及运算，程序之后将还会有详细的讲解操作过程的实现原理。

#include<stdio.h>
#include<stdlib.h>
typedef int ElemType;
struct HeapSq //定义堆的顺序存储类型
{
    ElemType* heap; //定义指向动态数组空间的指针
    int len; //定义保存堆长度的变量,即数组长度，数组下标从0开始
    int MaxSize;    //用于保存初始化时所给的动态数组空间的大小
};

//1、初始化堆
void InitHeap(struct HeapSq* HBT, int MS)
{
    if (MS <= )
    {
        printf("数组长度参数不合适，需重新给定！\n");
        exit();
    }
    HBT->heap = malloc(MS*sizeof(ElemType));
    if (!HBT->heap)
    {
        printf("用于动态分配的内存空间用完，退出运行！\n");
        exit();
    }
    HBT->MaxSize = MS;
    HBT->len = ;
}

//2、清除堆
void ClearHeap(struct HeapSq* HBT)
{
    if (HBT->heap != NULL)
    {
        free(HBT->heap);
        HBT->len = ;
        HBT->MaxSize = ;
    }
}

//3、检查一个堆是否为空
int EmptyHeap(struct HeapSq* HBT)
{
    if (HBT->len == )
        return ;
    else
        return ;
}

//4、向堆中插入一个元素
void InsertHeap(struct HeapSq* HBT, ElemType x)
{
    int i;
    if (HBT->len == HBT->MaxSize) //若堆满，将数组空间扩展为原来的2倍
    {
        ElemType *p;
        p = realloc(HBT->heap, *HBT->MaxSize*sizeof(ElemType));
        if (!p)
        {
            printf("存储空间用完！\n");
            exit();
        }
        printf("存储空间已扩展为原来的2倍！\n");
        HBT->heap = p;
        HBT->MaxSize = *HBT->MaxSize;
    }
    HBT->heap[HBT->len] = x; //向堆尾添加新元素
    HBT->len++; //堆长度加1
    i = HBT->len - ; //i指向待调整元素的位置，即其数组下标，初始指向新元素所在的堆尾位置
    while (i != )
    {
        int j = (i - ) / ; //j指向下标为i的元素的双亲
        if (x >= HBT->heap[j]) //若新元素大于待调整元素的双亲，则比较调整结束，退出循环
            break;
        HBT->heap[i] = HBT->heap[j]; //将双亲元素下移到待调整元素的位置
        i = j; //使待调整位置变为其双亲位置，进行下一次循环
    }
    HBT->heap[i] = x;//把新元素调整到最终位置
}

//5、从堆中删除堆顶元素并返回
ElemType DeleteHeap(struct HeapSq* HBT)
{
    ElemType temp, x;
    int i, j;
    if (HBT->len == )
    {
        printf("堆已空，退出运行！\n");
        exit();
    }
    temp = HBT->heap[]; //暂存堆顶元素
    HBT->len--;
    if (HBT->len == ) //若删除操作后堆为空则返回
        return temp;
    x = HBT->heap[HBT->len]; //将待调整的原堆尾元素暂存x中，以便放入最终位置
    i = ; //用i指向待调整元素的位置，初始指向堆顶位置
    j =  * i + ;//用j指向i的左孩子位置，初始指向下标为1的位置
    while (j <= HBT->len - )//寻找待调整元素的最终位置，每次使孩子元素上移一层，调整到孩子为空时止
    {
        if (j < HBT->len -  && HBT->heap[j] > HBT->heap[j+])//若存在右孩子且较小，使j指向右孩子
            j++;
        if (x <= HBT->heap[j]) //若x比其较小的孩子还小，则调整结束，退出循环
            break;
        HBT->heap[i] = HBT->heap[j];//否则，将孩子元素移到双亲位置
        i = j; //将待调整位置变为其较小的孩子位置
        j =  * i + ;//将j变为新的待调整位置的左孩子位置，继续下一次循环
    }
    HBT->heap[i] = x; //把x放到最终位置
    return temp; //返回原堆顶元素
}

//主函数
void main()
{
    int i, x;
    int a[] = {,,,,,,,};
    struct HeapSq b;
    InitHeap(&b, );
    for (i = ; i < ; i++)
        InsertHeap(&b, a[i]);
    while (!EmptyHeap(&b)) //依次删除堆顶元素并显示出来，直到堆空为止
    {
        x = DeleteHeap(&b);
        printf("%d", x);
        if (!EmptyHeap(&b))
            printf(",");
    }
    printf("\n");
    system("pause");
    ClearHeap(&b);
}

运行结果：

分析：

（1）讲下堆的插入操作：

向堆中插入一个元素时，首先将该元素写入到堆尾，即堆中最后一个元素后面（下标为 len 的位置上），然后调整为一个新堆。

调整方法：若新元素小于双亲结点的值，就让它们互换位置，新元素换到双亲位置后，使得以该位置为根的子树称为堆；

然后再对该位置与其双亲结点的值比较，做同样的调整，直到以新位置的双亲结点为根仍是一个堆，或者调整到堆顶为止，此时整个树变称为了一个堆。

上面的程序，依次将数组[23,56,40,62,38,55,10,16]的中的元素插入堆，插入过程如下：

我们拿其中一个步骤具体分析，比如插入最后一个元素16时，插入之前的示意图为上图中的倒数第二个图，在此图的基础上，将16插入堆尾，即62的左孩子位置，

此时16比其双亲62小，则使其与62互换位置，而此时16又比它所处的新位置的双亲38小，则再与38互换，最后此时16比它所处的新位置的双亲10大，则调整结束，

最后结果即为上图中的最后一个图所示。

（2）讲下堆的删除操作

删除操作是删除堆顶元素，留下的堆顶位置由堆尾位置填补，然后将其调整为一个新堆，

调整方法：新的堆顶元素值若大于两个孩子结点中的最小值，就将它与具有最小值的孩子结点互换位置，

在被换到孩子结点位置后，再对此位置与其孩子结点最小值比较，进行同样的调整，

直到以调整后的位置为根的子树称为一个堆，或者调整到叶子结点为止。

上面的程序依次删除堆顶元素的过程如下：

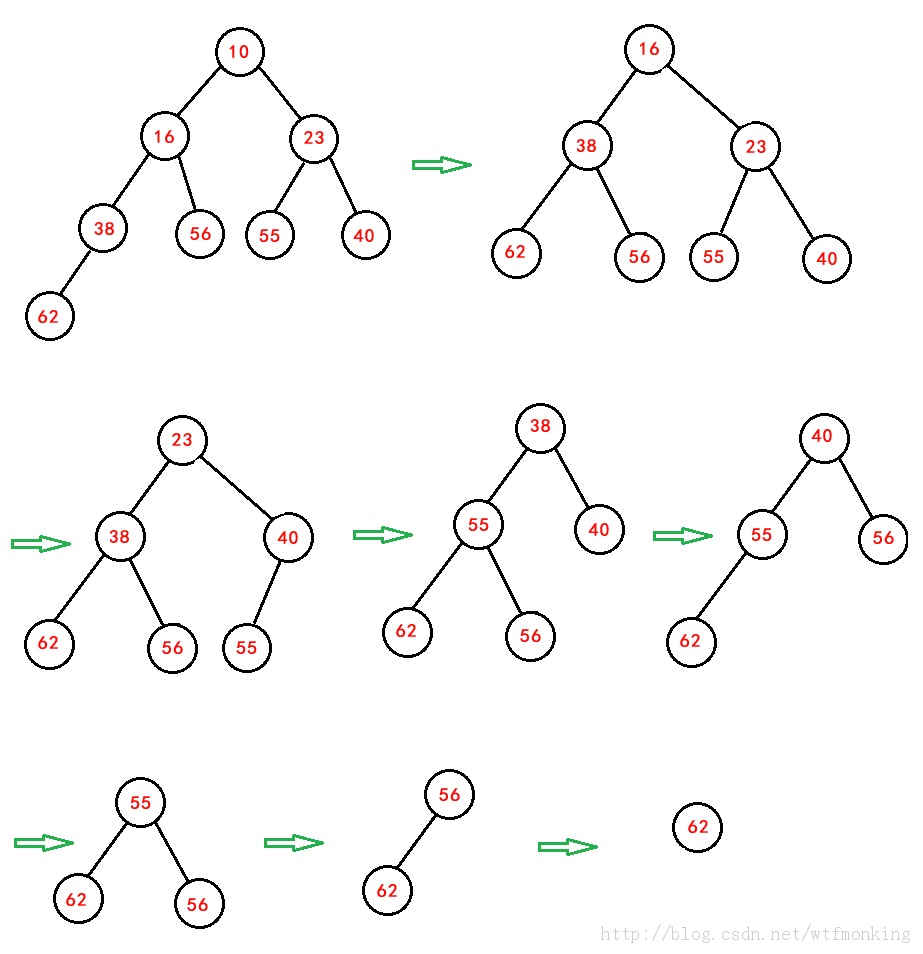
我们拿其中一个具体分析，如删除第一个堆顶元素10时，删除之前的示意图为上图中的第一个图，在此图的基础上，将10删除，然后将堆尾元素62放在堆顶，

此时，62比其所在位置的孩子的最小值16大，则将其与16位置互换，而此时62又比其所在位置的孩子的最小值38大，则将其与38位置互换，此时的62所在的位置是

叶子结点，调整结束，最后的结果为上图中的第二个图所示。