清北学堂dp图论营游记day4

依然zhx讲。

讲了概率与期望：

期望：事件结果的平均大小。记作E(x)。

E(x)=每种结果的大小与其概率的乘积的和。

例如，记掷一枚骰子的点数为x

E(x)=1*(1/6)+2*(1/6)+3*(1/6)+4*(1/6)+5*(1/6)+6*(1/6)=7/2

若c为常数，那么：

E(x+c)=E(x)+c，E(c*x)=c*E(x)。

如果记两个事件的结果分别为x,y，那么他们自然满足以下性质：

E(x+y)=E(x)+E(y)

例如：E(语文成绩+数学成绩)=E(语文成绩)+E(数学成绩)

若两个事件互相独立，E(x*y)=E(x)*E(y)

E(语文成绩*数学成绩)=E(语文成绩)*E(数学成绩)

其中，第一个性质在任何情况下满足，第二个一定要满足事件独立！

 

概率和期望的计算

概率与期望的计算有一个共同的计算技巧：

若事件所产生的所有方案都是等概率的，那么一些概率与期望即可转化

为一个计数问题，算出后再除以总方案数即可。

如求事件符合条件A的概率，则转化为对符合A的方案数的计数问题；若

求方案的某种价值的期望值，则转化为所有方案的价值总和的计数问题。

emmmmm。。。举个栗子qwq

概率与期望还可以通过列方程的方法计算。

有4张卡片，写着0,1,2,3，每次抽出一张并放回，反复抽，抽出0为止。问

抽取的次数的期望值。

设抽取次数为x，则：x=1+x*3/4

x=4。

 

上题：

 

 

对于每一个边，走过的概率为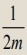

那么每个点的概率即为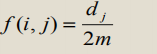

于是答案就是：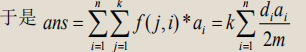

斜率优化：

万能套用代码： 。d+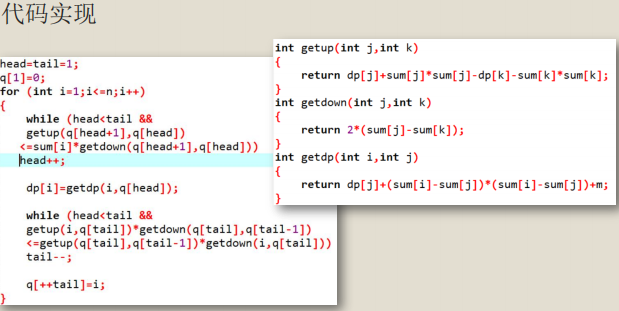

欢送赵和旭qwq。上午结束辣。

下午，恭迎杨思祺。

一个把poj（p欧接）念成poj（p欧勾）的神仙。

图论：

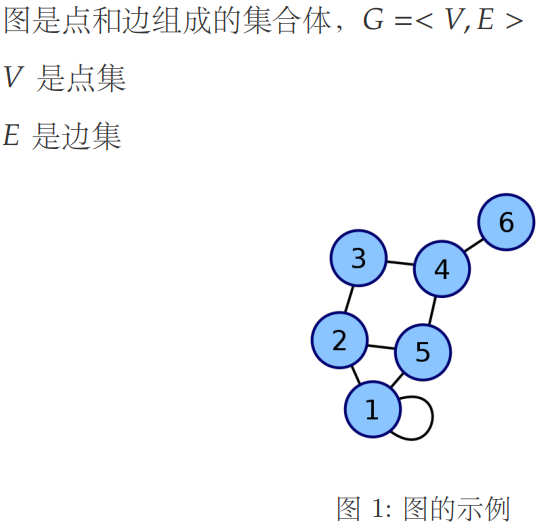
边：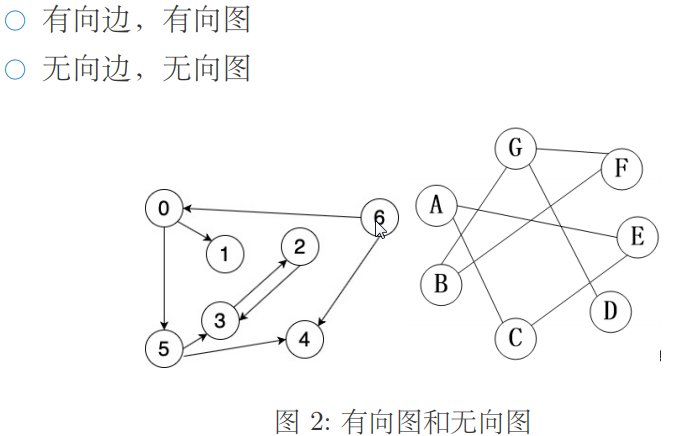

老师准备的很认真，开始知识很基础（shui）。

点权：赋给点的数值。

边权：赋给边的数值。

负权：边的权值为负。

有向无环图：dag（大哥）。

树：不用解释。。

完全图：任意两个点间都有一条直接相连的边。

竞赛图：有向边（版本）坂本的完全图

基环树：在树（n个节点，n-1条边）的基础上，任意加一条边（n个节点，n个边），有且仅有一个简单环。

仙人掌：存在环，但是任意一个边不属于两个环的图

邻接矩阵存图：

链式前向星（邻接表存图）

安利自己博客。

图的遍历：

二叉树遍历：

思路：构建最短路图并统计入度，如果入度大于1，就不影响。等于一，一定会影响。

裸拓扑排序。跑的时候判个环就行

上最短路：

分为全局（floyd）最短路，单源（dij，spfa）最短路。

dij:

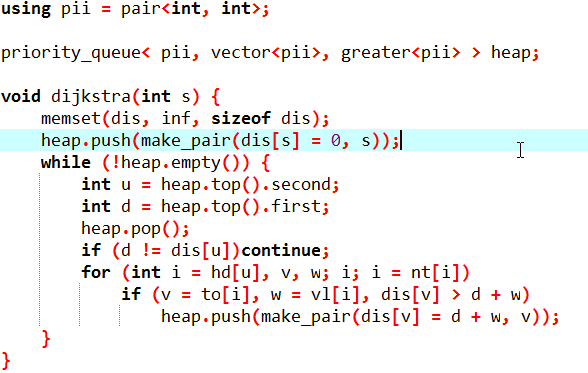
spfa:

今天就这样了，后半天还挺水的。。。。。

完结。