蒟蒻的splay 1---------洛谷板子题普通平衡树

前言部分

splay是个什么东西呢？

它就是个平衡树，支持以下操作

这些操作还可以用treap,替罪羊树，红黑树，multiset balabala(好像混进去什么奇怪的东西)

这里就只说一下splay（其他的窝不会）（splay窝也不会）

先来几个变量和一些辅助函数：

root:当前平衡树的根是那个节点

sz:整个平衡树的大小

ch[x][0]:x的左儿子的编号

ch[x][1]:x的右儿子的编号

size[x]:x和它的子树的大小

cnt[x]:编号为x的点的权值出现了几次

par[x]:x的父亲的编号

key[x]:编号为x的点的权值

get(x):查询x是它父亲的左儿子还是右儿子（左儿子返回0，右儿子返回1）

pushup(x):统计x的size和cnt

clear(x):将x的ch,size,cnt,key清0（删除用）

代码：

void pushup(int x)
{
    size[x]=size[ch[x][]]+size[ch[x][]]+cnt[x];//左子树+右子树+自身的cnt
    return ;
}

void clear(int x)
{
    size[x]=;ch[x][]=;ch[x][]=;key[x]=;cnt[x]=;par[x]=;
    return ;//全部清0就好辣
}

bool get(int x)
{
    return ((ch[par[x]][]==x)?:);//如果x是自己父亲的右儿子，就返回1，否则返回0
}

正文开始

一.一些基础操作

说了辣么多，还没有介绍平衡树到底是个什么东西

不过不着急，我们先来看看二叉搜索树

二叉搜索树有一个神奇的性质：所有比当前节点x权值小的节点，都在x的左子树里面，权值比x大的点都在x的右子树里

有了这个神奇的性质，在一般情况下树高就是log级别的，查询的复杂度也就降到了log级别，这很好对不对？

但是duliu出题人总是会种出一些歪七扭八的二叉搜索树,就像下面这样（节点里面的数是权值）

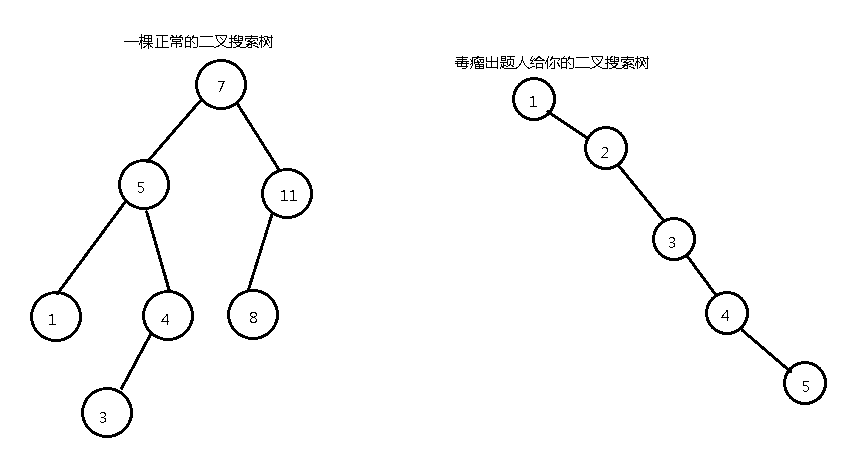
对于第二种毒瘤的二叉搜索树，复杂度就退化成了O(n),这不优美。我们想让它成长，让它学会自己平衡。于是，它成长成了平衡树。

splay如何做到自己平衡？

我们看这个丑陋的树：

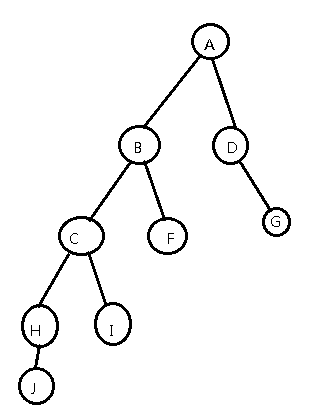
转一转(右旋)

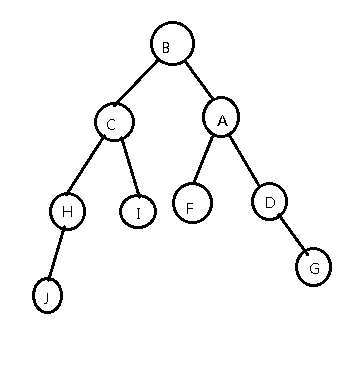
我们发现，B原本的右儿子成了A的左儿子，B现在的右儿子是A,其余不变

为什么这样转？

我们把B转成了根，那么B就没有父亲了，但是多了A这个右儿子，需要处理成二叉。同时A失去了左儿子，并且A发现B还有一个原来的右儿子F，F比A小，于是A就让F当自己的左儿子

如果我们把A左旋（然后这个树就更不平衡了ρωρ）

我们发现A没有右儿子了，D的左儿子变成了A

旋转的方式和右旋差不多，这里是让D的左儿子认A当爹，让A认D当爹。

不过可惜D并没有左儿子，于是A转完了也就没有右儿子辣。

我们可以总结出旋转的规律：

现在我们要把x转到根的位置（不管现在x在哪）

我们用k表示x是它父亲的左儿子还是右儿子（0是左儿子，1是右儿子）,y是x的儿子

就让y的k方向的儿子变成x的与k相反方向的儿子，y认x为爹，同时让y的父亲在y这个方向上的儿子替换成x

说人话版本：

y=par[x],z=par[y],k=get(x),e=get(y)

ch[y][k]=ch[x][k^1]

par[ch[y][k]]=y

par[y]=x

ch[x][k^1]=y

par[x]=z

ch[z][e]=x

代码版本：

void rotate(int x)
{
    int y=par[x],z=par[y],k=get(x),e=get(y);
    ch[y][k]=ch[x][k^];par[ch[y][k]]=y;
    par[y]=x;ch[x][k^]=y;
    par[x]=z;
    if(z)
     ch[z][e]=x;
     pushup(y);pushup(x);//记得pushup回去（统计信息）
}

当然只旋转一次是肯定不够的，所以我们再来一个splay函数。

splay(x)就是把x旋转到根（当然也可以再带一个参数，让x旋转到那个参数去）

定义fa，让fa一直等于当前x的父亲，一直旋转x,直到x的父亲是0（x是根节点）

注意：如果x，x的父亲，x的爷爷在同一条线上，就先转x的父亲

void splay(int x)
{
    for(int fa;fa=par[x];rotate(x))
        if(par[fa])
            rotate((get(x)==get(fa))?fa:x);
    root=x;
}

好像有什么不对的？？？

貌似这些操作一个都没有实现ρωρ

那就开始讲这些操作好了

二.平衡树支持的操作

1.插入X

如果当前平衡树里面没有元素，就直接sz++,root=sz

如果当前点的权值>x,就到左子树找x,反之则到右子树找，直到找到x，然后更新cnt,size,顺便再splay一下

如果找到最后都没有x,就说明x先前不在平衡树里，就新建一个节点，其权值为x，维护cnt,size

void insert(int x)
{
    if(root==)
    {
        sz++;
        key[sz]=x;
        root=sz;
        cnt[sz]=;size[sz]=;
        par[sz]=ch[sz][]=ch[sz][]=;
        return;//这里由于只有一个节点，就不需要splay了
    }
    int now=root,fa=;
    while()
    {
        if(key[now]==x)
               {
            cnt[now]++;
            pushup(now);//先更新now,再更新fa
            pushup(fa);
            splay(now); //为了以后方便，我们要把当前点splay到根
            return ;
        }
        fa=now;
        now=ch[now][key[now]<x];//第二维表示的是如果key[now]<x,就返回1，否则是0
        if(now==)//最终没有找着（不存在的节点默认值是0）
        {
            sz++;
            size[sz]=;cnt[sz]=;
            root=sz;
            key[sz]=x;
            ch[fa][key[fa]<x]=sz;
            par[sz]=fa;
            key[sz]=x;
            pushup(fa);
            splay(sz);return ;
        }
    }
}

插入

删除比较麻烦待会再说

2.查询x的排名

还是遵循key[now]比x小就往左子树找，否则就往右子树找的原则，直到找到

注意这里排名的定义是所有比x小的数的数量+1，如果有一个数q比x小，但是q出现了多次，那么重复出现的q也算作比x小的数（就是答案也包括那些重复出现的数辣）。

因此，往左子树搜，当前答案不变，往右子树搜，答案增加size[左子树]

因为重复的也算，所以在now转移前还要加cnt[now]

查到了要记得splay!!!

int findk(int x)
{
    int rtn=;
    int now=root;
    while()
    {
        if(key[now]>x)now=ch[now][];
        else
        {
            rtn+=(ch[now][]?size[ch[now][]]:);//先加（不管是否找到）
            if(x==key[now])
            {
                splay(now);//记住splay
                return rtn+;//记住+1
            }
            rtn+=cnt[now];
            now=ch[now][];
        }
    }
}

查询x的排名

3.查询第k大的数

k边查边减

如果当前点的左子树的size>=k,则去左子树查，k-=size[左子树]

否则就去右子树查，当now的size[左子树]+cnt[now]>=k的时候就说明now的权值就是第k大的数

因为如果当前的now不是第k大的话，就会去左子树查，但是现在已经是在右子树查的阶段了

int kth(int x)
{
    int now=root,rtn=;
    while()
    {
        if(ch[now][]&&size[ch[now][]]>=x)now=ch[now][];
           else
          {
            int temp=size[ch[now][]]+cnt[now];
            if(temp>=x)
            {
                return key[now];//这回不用splay了
        }
        x-=temp;now=ch[now][];
          }
    }
}

kth

4.找x的前驱/后继

我们在找前驱/后继之前先把x插入原平衡树种，找完以后再删掉，会很方便。

在插入中，我们已经把x splay到根了，所以我们在找前驱的时候，就从根的左儿子开始，一路找到左儿子右子树的叶子节点，就是前驱。

后继：从根的右儿子开始，一路找到右儿子的左子树的叶子节点即可

int pre()
{
    int now=ch[root][];
    while(ch[now][])now=ch[now][];
    return now;
}
int next()
{
    int now=ch[root][];
    while(ch[now][])now=ch[now][];
    return now;
}

找前驱/后继

5.最复杂的删除X

情况比较多，咱慢慢来

先来一次findk(x),目的是把x旋到根（也可以直接splay(x)）

1：x曾经出现过多次

对于这种情况，直接cnt--,size--

2:x只出现过1次

①：x没有儿子：直接clear(root)

②：x只有左儿子或者右儿子

让x唯一的儿子当根，并调整父子关系（x的儿子没有父亲神马的），clear(x)

③：最麻烦的情况，x两个儿子都有

把x的前驱转到根，让x的前驱继承x的右儿子（至于左儿子，在把x的前驱转到根的时候已经继承了），调整父子关系（x的右儿子认x的前驱神马的），clear(x)

void del(int x)
{
    int sy=fink(x);
    if(cnt[root]>)
    {
        cnt[root]--;pushup(root);return;
    }
    if(!ch[root][]&&!ch[root][])
    {
        clear(root);root=;return ;
    }
    if(!ch[root][])
    {
        int rt=root;root=ch[root][];par[root]=;clear(rt);return ;
    }
    else if(!ch[root][])
    {
        int rt=root;root=ch[root][];par[root]=;clear(rt);return ;
    }
    int rt=root;int pr=pre();
    splay(pr);
    ch[root][]=ch[rt][];
    par[ch[rt][]]=root;
    clear(rt);
    pushup(root);
}

删除x

模板题：洛谷P3369普通平衡树

更难一点的窝不会的文艺平衡树

#include<bits/stdc++.h>
#define pa pair<int,int>
using namespace std;
inline int read()
{
    char ch=getchar();
    int x=;bool f=;
    while(ch<''||ch>'')
    {
        if(ch=='-')f=;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        x=(x<<)+(x<<)+(ch^);
        ch=getchar();
    }
    return f?-x:x;
}
const int N=;
int n,sz;
int ch[N][],par[N],key[N],cnt[N],size[N];
int root;
void pushup(int x)
{
    size[x]=size[ch[x][]]+size[ch[x][]]+cnt[x];
    return ;
}
void clear(int x)
{
    size[x]=;ch[x][]=;ch[x][]=;key[x]=;cnt[x]=;par[x]=;
    return ;
}
bool get(int x)
{
    return ((ch[par[x]][]==x)?:);
}
void rotate(int x)
{
    int y=par[x],z=par[y],k=get(x),e=get(y);
    ch[y][k]=ch[x][k^];par[ch[y][k]]=y;
    par[y]=x;ch[x][k^]=y;
    par[x]=z;
    if(z)
     ch[z][e]=x;
     pushup(y);pushup(x);
}
void splay(int x)
{
    for(int fa;fa=par[x];rotate(x))
        if(par[fa])
            rotate((get(x)==get(fa))?fa:x);  

    root=x;
}
void insert(int x)
{
    if(root==)
    {
        sz++;
        key[sz]=x;
        root=sz;
        cnt[sz]=;size[sz]=;
        par[sz]=ch[sz][]=ch[sz][]=;
        return;
    }
    int now=root,fa=;
    while()
    {
        if(key[now]==x)
        {
            cnt[now]++;
            pushup(now);
            pushup(fa);
            splay(now);//当前节点旋转
            return ;
        }
        fa=now;
        now=ch[now][key[now]<x];
        if(now==)
        {
            sz++;
            size[sz]=;cnt[sz]=;
            root=sz;
            key[sz]=x;
            ch[fa][key[fa]<x]=sz;
            par[sz]=fa;
            key[sz]=x;
            pushup(fa);
            splay(sz);return ;
        }
    }
}
int fink(int x)
{
    int rtn=;
    int now=root;
    while()
    {
        if(key[now]>x)now=ch[now][];
        else
        {
            rtn+=(ch[now][]?size[ch[now][]]:);
            if(x==key[now])
            {
                splay(now);
                return rtn+;
            }
            rtn+=cnt[now];
            now=ch[now][];
        }
    }
}
int kth(int x)
{
    int now=root,rtn=;
    while()
    {
        if(ch[now][]&&size[ch[now][]]>=x)now=ch[now][];
        else
        {
            int temp=size[ch[now][]]+cnt[now];
            if(temp>=x)
            {
                return key[now];
            }
            x-=temp;now=ch[now][];
        }
    }
}
int pre()
{
    int now=ch[root][];
    while(ch[now][])now=ch[now][];
    return now;
}
int next()
{
    int now=ch[root][];
    while(ch[now][])now=ch[now][];
    return now;
}
void del(int x)
{
    int sy=fink(x);
    if(cnt[root]>)
    {
        cnt[root]--;pushup(root);return;
    }
    if(!ch[root][]&&!ch[root][])
    {
        clear(root);root=;return ;
    }
    if(!ch[root][])
    {
        int rt=root;root=ch[root][];par[root]=;clear(rt);return ;
    }
    else if(!ch[root][])
    {
        int rt=root;root=ch[root][];par[root]=;clear(rt);return ;
    }
    int rt=root;int pr=pre();
    splay(pr);
    ch[root][]=ch[rt][];
    par[ch[rt][]]=root;
    clear(rt);
    pushup(root);
}
int main()
{
   n=read();
   for(int i=;i<=n;i++)
   {
       int opt=read(),x=read();;
       if(opt==)insert(x);
       if(opt==)del(x);
       if(opt==)printf("%d\n",fink(x));
       if(opt==)printf("%d\n",kth(x));
       if(opt==){insert(x);printf("%d\n",key[pre()]);del(x);}
       if(opt==){insert(x);printf("%d\n",key[next()]);del(x);}
   }
}

这是P3369的代码ρωρ