hdu 5791 思维dp

题目描述：

求序列A,B的公共子序列个数；

基本思路：

想到了dp，选的状态也对，但是就是就是写不出状态转移方程，然后他们都出了，到最后我还是没出，很难受，然后主要是没有仔细考虑dp【i】【j】，dp【i】【j-1】，dp【i-1】【j】，dp【i-1】【j-1】在A【

i】和B【i】在相同和不相同是的数量关系，我为啥就没想到要减呢，只想着怎么把他们加起来，着实智障；

定义状态dp【i】【j】为序列A扫到i，序列B扫到B时候的公共子序列个数，状态转移方程如下：

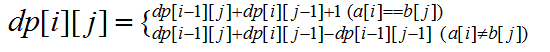
其实这个状态转移方程也没那么好证明，但仔细想一想，如果相等的话，不过就是dp【i】【j-1】和dp【i-1】【j】的公共部分和a【i】和b【j】这一对组合，这公共部分在dp【i】【j-1】和dp【i-1】【j】中必定是重合的，然后就是还有a【i】和b【j】这一对组合单独着，然后状态转移方程就是上面第一个状态转移方程这样，然后第二个也是一样的考虑方式；（说实话把他放到简单dp里，我还是很羞愧的）；

代码如下：

#include<iostream>
#include<sstream>
#include<iomanip>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<stack>
#include<list>
#include<map>
#include<set>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>

using namespace std;

typedef long long ll;
typedef long double ld;
#define rep(a,b,c) for(int (a)=(b);(a)<=(c);(a)++)
#define drep(a,b,c) for(int (a)=(b);(a)=>(c);(a)--)
const int inf = 0x3f3f3f3f;
const double eps = 1e-;
const int mod = ;

const int maxn = +;
ll dp[maxn][maxn];
int s[maxn],t[maxn];

int main()
{
    int n,m;
    while(scanf("%d%d",&n,&m)==)
    {
        memset(dp,,sizeof(dp));
        for(int i=;i<=n;i++) scanf("%d",&s[i]);
        for(int j=;j<=m;j++) scanf("%d",&t[j]);
        for(int i=;i<=n;i++)
        {
            for(int j=;j<=m;j++)
            {
                if(s[i]==t[j])
                {
                    dp[i][j]=(dp[i-][j]+dp[i][j-]++mod)%mod;
                }
                else
                {
                    dp[i][j]=(dp[i][j-]+dp[i-][j]-dp[i-][j-]+mod)%mod;
                }
            }
        }
        printf("%I64d\n",dp[n][m]);
    }
    return ;
}