Hihocoder #1077 : RMQ问题再临-线段树(线段树：结构体建树+更新叶子往上+查询+巧妙使用father[]+线段树数组要开大4倍 *【模板】)

#1077 : RMQ问题再临-线段树

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

上回说到：小Hi给小Ho出了这样一道问题：假设整个货架上从左到右摆放了N种商品，并且依次标号为1到N，每次小Hi都给出一段区间[L, R]，小Ho要做的是选出标号在这个区间内的所有商品重量最轻的一种，并且告诉小Hi这个商品的重量。但是在这个过程中，可能会因为其他人的各种行为，对 某些位置上的商品的重量产生改变（如更换了其他种类的商品）。

小Ho提出了两种非常简单的方法，但是都不能完美的解决。那么这一次，面对更大的数据规模，小Ho将如何是好呢？

提示：其实只是比ST少计算了一些区间而已

输入

每个测试点（输入文件）有且仅有一组测试数据。

每组测试数据的第1行为一个整数N，意义如前文所述。

每组测试数据的第2行为N个整数，分别描述每种商品的重量，其中第i个整数表示标号为i的商品的重量weight_i。

每组测试数据的第3行为一个整数Q，表示小Hi总共询问的次数与商品的重量被更改的次数之和。

每组测试数据的第N+4~N+Q+3行，每行分别描述一次操作，每行的开头均为一个属于0或1的数字，分别表示该行描述一个询问和描述一次商品的重 量的更改两种情况。对于第N+i+3行，如果该行描述一个询问，则接下来为两个整数Li, Ri，表示小Hi询问的一个区间[Li, Ri]；如果该行描述一次商品的重量的更改，则接下来为两个整数Pi，Wi，表示位置编号为Pi的商品的重量变更为Wi

对于100%的数据，满足N<=10^6，Q<=10^6, 1<=Li<=Ri<=N，1<=Pi<=N, 0<weight_i, Wi<=10^4。

输出

对于每组测试数据，对于每个小Hi的询问，按照在输入中出现的顺序，各输出一行，表示查询的结果：标号在区间[Li, Ri]中的所有商品中重量最轻的商品的重量。

样例输入

10
3655 5246 8991 5933 7474 7603 6098 6654 2414 884
6
0 4 9
0 2 10
1 4 7009
0 5 6
1 3 7949
1 3 1227

样例输出

2414
884
7474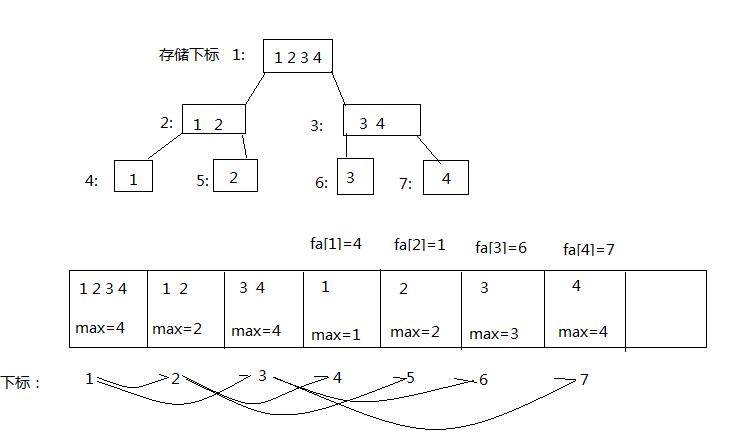

上面是我自己制作的简单的线段树的存储结构图

线段树的基础题，考的是线段树的数据结构实现。不讲算法
代码：

#include <stdio.h>
#include <string.h>
#include <math.h>
#include <iostream>
#include <string>
#include <algorithm>

using namespace std;
struct node
{
    int ll; int rr;
    int mm;
}q[4000010];
int fa[1000002];

void Build_ST(int i, int ll, int rr )
{
    q[i].ll=ll;
    q[i].rr=rr;
    q[i].mm=210000000;
    if(ll == rr ) //
    {
        fa[ll] = i; //
        return ;
    }
    Build_ST(i*2, ll, (ll+rr)/2 );
    Build_ST(i*2+1, (ll+rr)/2+1, rr );
}

void update_ST(int ri) //自下向上更新 输入的是底层节点的编号
{
    if(ri==1)
    {
        return ; //表示该底层节点是根节点 修改完成 返回
    }
    //如果不是根节点 就一直往上修改 直到修改到根节点
    int fi; //
    fi=ri/2;
    q[fi].mm = min( q[fi*2].mm, q[fi*2+1].mm ); //此处必须写成fi*2和fi*2+1的形式，因为整数除法精度问题，写成ri和ri+1会错的
    update_ST(ri/2);
}
int Min;
void query(int i, int ll, int rr )
{
    if(q[i].ll==ll && q[i].rr==rr )//
    {
        Min= min(Min, q[i].mm );
        return ;
    }
    i=i<<1;
    if(ll<=q[i].rr )
    {
        if(rr<=q[i].rr )
        {
            query(i, ll, rr);
        }
        else
        {
            query(i, ll, q[i].rr );
        }
    }
    i=i+1;
    if(rr>=q[i].ll )
    {
        if(ll>=q[i].ll )
        {
            query(i, ll, rr );
        }
        else
        {
            query(i, q[i].ll, rr );
        }
    }
}

int main()
{
    int n, m;
    scanf("%d", &n);
    Build_ST(1, 1 , n);//

    int i, j;
    int dd;
    for(i=1; i<=n; i++)
    {
        scanf("%d", &dd );
        q[fa[i]].mm = dd;
        update_ST(fa[i]);
    }
    scanf("%d", &m);
    int pos, num;
    int left, right;

    for(j=0; j<m; j++ )
    {
        scanf("%d", &dd);
        if(dd==0) //xun wen
        {
            scanf("%d %d", &left, &right );
            Min=210000000;
            query(1, left, right );
            printf("%d\n", Min );
        }
        else if(dd==1)
        {
            scanf("%d %d", &pos, &num ); //因为题目的原因，一定修改的是某个叶子节点的信息
            q[fa[pos]].mm=num;
            update_ST(fa[pos]);
        }
    }
    return 0;
}

2015/8/18 重新写了

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <ctype.h>
#include <math.h>
#include <queue>
#include <iostream>
#include <algorithm>
#define INF 0x3f3f3f3f

using namespace std;
struct node
{
    int ll, rr;
    int mm;//保存最大值
}q[4000000+10];

int fa[1000000+2];

/*
  线段树是一种树状的数据结构，但在算法的实现过程中，
  用的是一维结构体数组来模拟的，
 */
void Build(int i, int ll, int rr)
{
    q[i].ll=ll;
    q[i].rr=rr;//当前线段节点的左右区间
    q[i].mm=INF;
    if(ll==rr){
        fa[ll]=i;
        return;
    }//如果当前的是叶子节点
     //fa[]记录下了每个叶子节点的存储位置
     Build(i*2, ll, (ll+rr)/2);
     Build(i*2+1, (ll+rr)/2+1, rr);
}  //往下递归两个儿子节点

void update(int ri)
{
    if(ri==1){
        return ;
    }//到达根节点 修改完成返回
    int fi=ri/2;
    q[fi].mm=min(q[fi*2].mm, q[fi*2+1].mm);
    update(ri/2);
}

int Min;
void query(int i, int ll ,int rr)
{
    if(q[i].ll==ll&&q[i].rr==rr){
        Min=min(Min, q[i].mm);
        return;
    }//
    i=i*2;
    if(ll<=q[i].rr){//在这个子节点有范围
        if(rr<=q[i].rr){
            query(i, ll, rr);
        }else{
            query(i, ll, q[i].rr);
        }
    }
    i=i+1;
    if(rr>=q[i].ll){
        if(ll>=q[i].ll ){
            query(i, ll, rr);
        }else{
            query(i, q[i].ll, rr);
        }
    }
}

int main()
{
    int n, m;//
    scanf("%d", &n);
    Build(1,1,n);

    int i, j, cur;
    for(i=1; i<=n; i++){
        scanf("%d", &cur);
        q[fa[i]].mm=cur;
        update(fa[i]);
    }//fa[i]是叶子节点的下标位置

    scanf("%d", &m);//m次操作
    int left, right;
    int pos, num;
    for(i=0; i<m; i++){
        scanf("%d", &cur);
        if(cur==0){//询问区间最小值
           scanf("%d %d", &left, &right);
           Min=INF;
           query(1, left, right);
           printf("%d\n", Min);
        }else{
            scanf("%d %d", &pos, &num);
            q[fa[pos]].mm=num;
            update(fa[pos]);
        }
    }
    return 0;
}