浅谈单调栈 By cellur925

这位dalao的单调栈文章很棒！我写的是他的题单233. http://www.cnblogs.com/COLIN-LIGHTNING/p/8474668.html

一、单调栈的一般写法

    for(int i=;i<=n;i++)
    {
        int x=;
        scanf("%d",&x);
        while(x>=sta[top]&&top)
            top--;
        sta[++top]=x;
    }

而各种各样繁杂的题目正是在这个基础上维护一些其他的信息。

二、注意事项

栈不能为空。要随时注意，否则RE。

计数类可能会用到$longlong$。

三、例题详解

例题0 LIS（最长上升子序列）辣个$nlogn$的算法其实本质上就是单调栈...

例题1 音乐会的等待

N个人正在排队进入一个音乐会。人们等得很无聊，于是他们开始转来转去，想在队伍里寻找自己的熟人。队列中任意两个人A和B，如果他们是相邻或他们之间没有人比A或B高，那么他们是可以互相看得见的。

写一个程序计算出有多少对人可以互相看见。（注意，是互相看见）

维护一个单调不增的栈。（因为两个之间没有比他们高的人时他们才能互相看见，中间隔等高个人时是可以互相看见的）

（注意！脑子别晕！233，这是栈！不是队列！栈顶是最后加的！）

当新来的人身高小于栈顶，直接进来。答案在栈非空的情况下加1，这算的是栈顶和当前元素这对。（满足相邻的条件）

当新来的人身高大于栈顶，弹栈直到满足小于（或等于）。因为维护的单调递减的栈，而新生还很高，所以自然能看得见。这里每次弹栈都加上那个元素的个数（具体接下来会讲）。满足性质后，再和栈顶比较。

当新来的人身高等于栈顶，弹栈直到小于。我们把和它相等的都弹走，但是要注意记上和它相等的数出现的次数，以便之后使用，因为相等，所以肯定看的见，为接下来记录了信息（解释了第二种情况）。满足性质后，再和栈顶比较。

综上，我们看出每个元素最多入栈出栈一次，复杂度$O(N)$，每次入栈后，都要在栈不为空的情况下，答案++，因为栈顶（最外面的元素）一定能看见新来的元素。

Code

 #include<cstdio>
 #include<algorithm>

 using namespace std;
 typedef long long ll;

 int n,top,x,num;
 struct node{
     int val,num;
 }sta[];
 ll ans;

 int main()
 {
     scanf("%d",&n);
     for(int i=;i<=n;i++)
     {
         scanf("%d",&x);
         node p=(node){x,};
         while(x>=sta[top].val&&top)
         {
             ans+=sta[top].num;
             if(sta[top].val==x) p.num+=sta[top].num;
             //虽然弹走了 记下  以后用得到
             top--;
         }
         if(top) ans++;
         sta[++top]=p;
     }
     printf("%lld",ans);
     return ;
 }

例题2 [POI2008]PLA-Postering

Byteburg市东边的建筑都是以旧结构形式建造的:建筑互相紧挨着,之间没有空间.它们共同形成了一条长长的,从东向西延伸的建筑物链(建筑物的高度不一).Byteburg市的市长Byteasar,决定将这个建筑物链的一侧用海报覆盖住.并且想用最少的海报数量,海报是矩形的.海报与海报之间不能重叠,但是可以相互挨着(即它们具有公共边),每一个海报都必须贴近墙并且建筑物链的整个一侧必须被覆盖(意思是:海报需要将一侧全部覆盖,并且不能超出建筑物链，即不能盖着没有海报存在的地方)

读完题后，我们很快就会发现，那个宽度的条件其实是没用的，我们只需要考虑高度就行了。设开始我们需要海报的数量等于矩形的数量，我们再一点点减。那么，我们便可以维护一个高度单调递增的栈，在弹栈过程中，若遇到和自己相等的高度，就将答案减去1，因为如图，我们可以横着盖，我们只需要再把高出来的（於出来的）用一张海报即可。

Code

 #include<cstdio>
 #include<algorithm>

 using namespace std;

 int n,ans,top;
 int sta[];

 int main()
 {
     scanf("%d",&n);
     for(int i=;i<=n;i++)
     {
         int y=,x=;
         scanf("%d%d",&y,&x);
         while(top&&x<=sta[top])
         {
             if(x==sta[top]) ans++;
             top--;
         }
         sta[++top]=x;
     }
     printf("%d",n-ans);
     return ;
 }

---

以上都是一些比较简单的线性问题。接下来我们要看的是那些或者在二维上，或者掺杂入实际的面积，这些更复杂的问题。

例题3 玉蟾宫 哎又要看Freda学姐和rainbowcat虐狗了

其实这题还有悬线法，是求最大子矩阵的一个方法，这里就不再说了==（大坑）

抽象一下本题的模型：有障碍点的情况下的最大子矩形。

虽然这题是二维的了，但是我们还可以分别计算情况。

首先，我们用一个$f[i][j]$表示在$(i,j)$点，前$i$行，第$j$列，以第$i$行结尾，连续的‘F’个数。（最大可延伸距离）

行与行之间的问题就解决了。

然后在同一行，不同列上的问题就可以用单调栈（单调递增栈）来维护了。

单调栈中存储两个信息。此单位高度$height$，和对应可控宽度$wid$（对应可控我觉得说的非常准确）

同理，我们当前的高度(f数组)大于栈顶时，直接把它压入栈。

否则，就一直弹栈。弹栈的时候，我们要记录矩形的信息来更新答案。它的$wid$是所有弹栈元素的$wid$+1.（因为我们继承了之前的信息，这部分 到之后也是可以用的。因为被弹栈的元素高度均大于当前元素，在可控范围内。）

之后更新答案即可。枚举到最后一列后，把栈都搞空。

Code

 #include<cstdio>
 #include<algorithm>

 using namespace std;

 int n,m,ans,top,tmp,neww;
 struct node{
     int height,wid;
 }sta[];
 char qwq[],mapp[][],f[][];

 void work(int x)
 {
     top=;tmp=;neww=;
     sta[].height=f[x][];
     sta[].wid=;
     for(int i=;i<=m;i++)
     {
         tmp=;
         while(f[x][i]<=sta[top].height&&top)
         {
             tmp+=sta[top].wid;
             neww=max(neww,tmp*sta[top].height);
             top--;
         }
         sta[++top].height=f[x][i];
         sta[top].wid=tmp+;
     }
     tmp=;
     while(top)
     {
         tmp+=sta[top].wid;
         neww=max(neww,tmp*sta[top].height);
         top--;
     }
     ans=max(ans,neww);
 }

 int main()
 {
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++)
         for(int j=;j<=m;j++)
         {
             scanf("%s",qwq+),mapp[i][j]=qwq[];
             if(mapp[i][j]=='F') f[i][j]=f[i-][j]+;
         }
     for(int i=;i<=n;i++) work(i);
     printf("%d",ans*);
     return ;
 }

例题4 Largest Rectangle in a Histogram

在一条水平线上给出若干连续矩形，求包含于这些矩形的并集内部最大矩形的面积。

这应该是单调栈的典型题目惹qwq。

我们假设，到现在为止，读入的矩形高度都是递增的，那么如果突然读入了一个比上一个矩形矮的矩形，那么之前高的矩形搞出来就没有用了（於出来了）

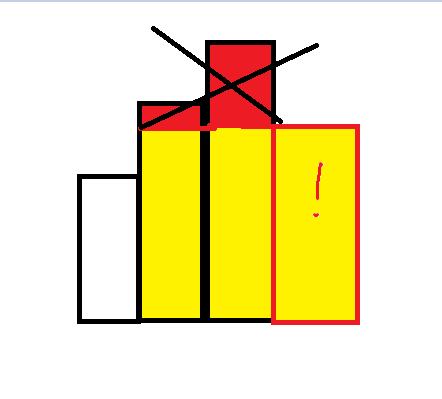
打叉的部分就没用了。没用就删去啊，所以我们在做的事情就是维护一个单调递增的矩形序列。与上题相似，弹矩形的时候，我们同样要维护弹出矩形的答案。

其实这和上一题差不多啦qwq。

Code

 #include<cstdio>
 #include<algorithm>
 #include<cstring>

 using namespace std;
 typedef long long ll;

 int n,top,x,tmp;
 ll ans;
 struct node{
     int height,wid;
 }sta[];

 int main()
 {
     while(scanf("%d",&n)!=EOF&&n)
     {
         for(int i=;i<=n;i++)
         {
             tmp=;
             scanf("%d",&x);
             while(x<=sta[top].height&&top)
             {
                 tmp+=sta[top].wid;
                 ans=max(ans,1ll*tmp*sta[top].height);
                 top--;
             }
             sta[++top].height=x;
             sta[top].wid=tmp+;
         }
         tmp=;
         while(top)
         {
             tmp+=sta[top].wid;
             ans=max(ans,1ll*tmp*sta[top].height);
             top--;
         }
         printf("%lld\n",ans);
         top=;ans=;
         memset(sta,,sizeof(sta));
     }
     return ;
 }

这种更新面积（我也不知道怎么总结）的问题，最后一定要记得把栈搞空啊qwq。

单调栈先告一段落，下一次来看单调队列qwq。