MyCAT学习总结

MyCAT介绍

简单的说，MyCAT就是：

一个彻底开源的，面向企业应用开发的“大数据库集群”

支持事务、ACID（指数据库事务正确执行的四个基本要素的缩写。包含:原子性(Atomicity)、一致性(Consistency)、隔离性(Isolation)、持久性(Durability)）、可以替代Mysql的加强版数据库

一个可以视为“Mysql”集群的企业级数据库，用来替代昂贵的Oracle集群

一个融合内存缓存技术、Nosql技术、HDFS大数据的新型SQL Server

结合传统数据库和新型分布式数据仓库的新一代企业级数据库产品

一个新颖的数据库中间件产品

MyCAT的目标是：低成本的将现有的单机数据库和应用平滑迁移到“云”端，解决数据存储和业务规模迅速增长情况下的数据瓶颈问题。

MyCAT的关键特性

支持 SQL 92标准

支持Mysql集群，可以作为Proxy使用

支持JDBC连接ORACLE、DB2、SQL Server，将其模拟为MySQL  Server使用

支持galera for mysql集群，percona-cluster或者mariadb cluster，提供高可用性数据分片集群

自动故障切换，高可用性

支持读写分离，支持Mysql双主多从，以及一主多从的模式

支持全局表，数据自动分片到多个节点，用于高效表关联查询

支持独有的基于E-R 关系的分片策略，实现了高效的表关联查询

多平台支持，部署和实施简单

MyCAT架构

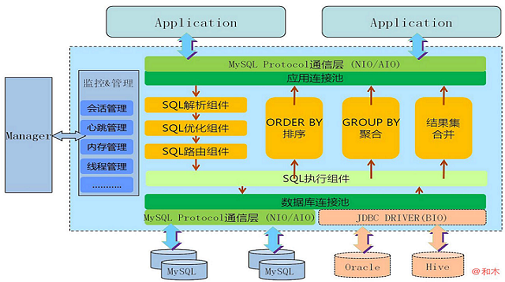
Mycat解决的问题

l  性能问题

l  数据库连接过多

l  E-R分片难处理

l  可用性问题

l  成本和伸缩性问题

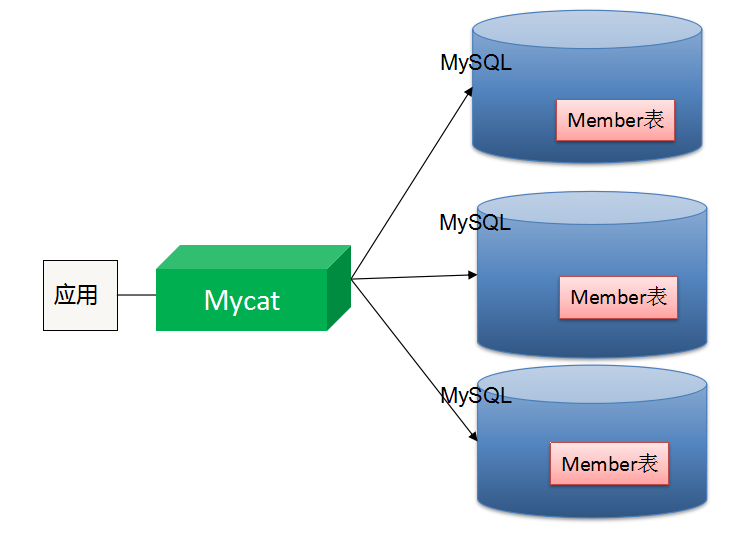
分片策略

MyCAT支持水平分片与垂直分片：

水平分片：一个表格的数据分割到多个节点上，按照行分隔。

垂直分片：一个数据库中多个表格A，B，C，A存储到节点1上，B存储到节点2上，C存储到节点3上。

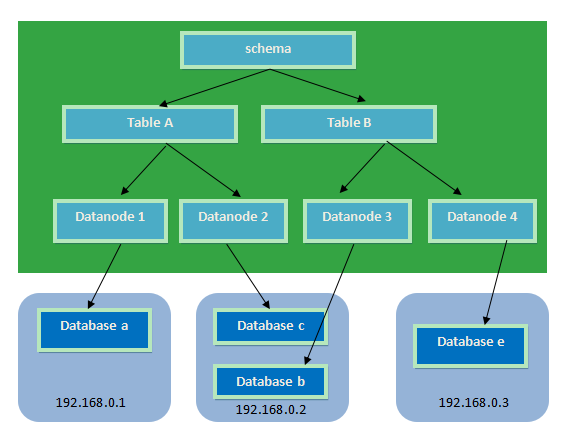
MyCAT通过定义表的分片规则来实现分片，每个表格可以捆绑一个分片规则，每个分片规则指定一个分片字段并绑定一个函数，来实现动态分片算法。

1、Schema：逻辑库，与MySQL中的Database（数据库）对应，一个逻辑库中定义了所包括的Table。

2、Table：表，即物理数据库中存储的某一张表，与传统数据库不同，这里的表格需要声明其所存储的逻辑数据节点DataNode。在此可以指定表的分片规则。

3、DataNode：MyCAT的逻辑数据节点，是存放table的具体物理节点，也称之为分片节点，通过DataSource来关联到后端某个具体数据库上

4、DataSource：定义某个物理库的访问地址，用于捆绑到Datanode上

mycat分片策略：

一  global-全局表

指定type为global，该表在所有的db存储的数据一致。

一  sharding-by-intfile

某些业务，不同的省，存储在不同的database中。

columns:表示字段

algorithm:指定方法

一  mod-long

求余数

一  crc32slot

注意：指定此分片规则，表格需重建。（自动添加_slot字段）

一  sharding-by-murmur

一致性hash

一  sharding-by-month

一  auto-sharding-long

根据指定的范围进行分片

Mycat读写分离

数据库读写分离对于大型系统或者访问量很高的互联网应用来说，是必不可少的一个重要功能。对于MySQL来说，标准的读写分离是主从模式，一个写节点Master后面跟着多个读节点，读节点的数量取决于系统的压力，通常是1-3个读节点的配置

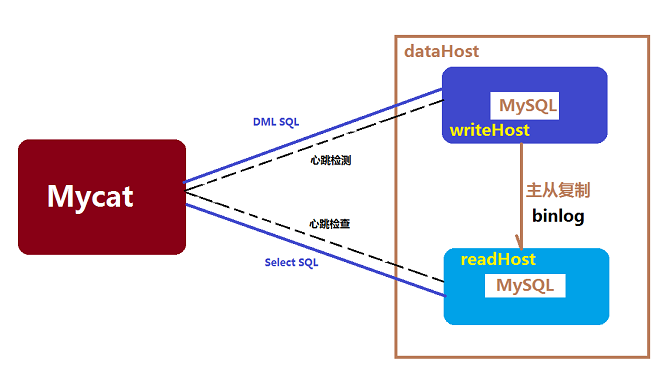
Mycat读写分离和自动切换机制，需要mysql的主从复制机制配合。

Mysql的主从复制

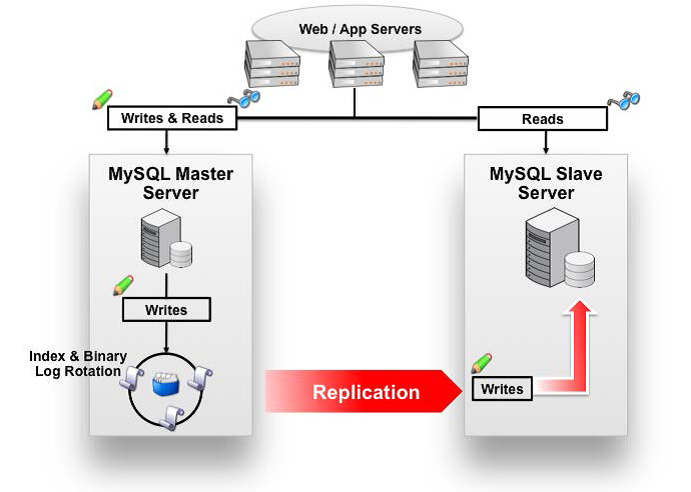
主从配置需要注意的地方

1、主DB server和从DB server数据库的版本一致

2、主DB server和从DB server数据库数据一致[ 这里就会可以把主的备份在从上还原，也可以直接将主的数据目录拷贝到从的相应数据目录]

3、主DB server开启二进制日志,主DB server和从DB server的server_id都必须唯一