回溯算法 DFS深度优先搜索（递归与非递归实现）

回溯法是一种选优搜索法（试探法），被称为通用的解题方法，这种方法适用于解一些组合数相当大的问题。通过剪枝（约束+限界）可以大幅减少解决问题的计算量（搜索量）。

基本思想

将n元问题P的状态空间E表示成一棵高为n的带权有序树T，把在E中求问题P的解转化为在T中搜索问题P的解。

深度优先搜索（Depth-First-Search，DFS）是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。 --from wiki

实现方法

1、按选优条件对T进行深度优先搜索，以达到目标。

2、从根结点出发深度优先搜索解空间树

3、当探索到某一结点时，要先判断该结点是否包含问题的解

如果包含，就从该结点出发继续按深度优先策略搜索
否则逐层向其祖先结点回溯（退回一步重新选择）
满足回溯条件的某个状态的点称为“回溯点”

4、算法结束条件

求所有解：回溯到根，且根的所有子树均已搜索完成
求任一解：只要搜索到问题的一个解就可以结束

遍历过程

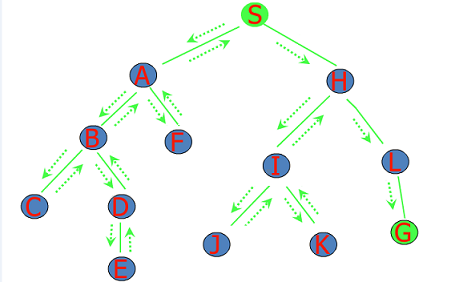
典型的解空间树

第一类解空间树：子集树

当问题是：从n个元素的集合S中找出满足某种性质的子集时相应的解空间树称为子集树，例如n个物品的0/1背包问题。

这类子集树通常有2^n个叶结点
解空间树的结点总数为2^(n+1) - 1
遍历子集树的算法需Ω(2^n)计算时间

第二类解空间树：排列树

当问题是：确定n个元素满足某种性质的排列时相应的解空间树称为排列树，例如旅行商问题。

DFS搜索在程序中可以两种方式来实现，分别是非递归方式和递归方式。前者思路更加清晰，便于理解，后者代码更加简洁高效。

非递归实现

非递归实现需要借助堆栈(先入后出，后入先出)，在C++中使用stack容器即可。

问题

若给定一个序列，需要找到其中的一个子序列，判断是否满足一定的条件。下面将程序实现DFS对子序列的搜索过程。

实现步骤：

1、首先将根节点放入堆栈中。

2、从堆栈中取出第一个节点，并检验它是否为目标。

如果找到目标，则结束搜寻并回传结果。
否则将它某一个尚未检验过的直接子节点加入堆栈中。

3、重复步骤2。

4、如果不存在未检测过的直接子节点。

将上一级节点加入堆栈中。
重复步骤2。

5、重复步骤4。

6、若堆栈为空，表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。

C++代码

/*********************************************************************

*

* Ran Chen <wychencr@163.com>

*

* Back-track algorithm （by DFS）

*

*********************************************************************/

#include <iostream>

#include <vector>

#include <stack>

using namespace std;

class Node

{

public:

	int num;  // 节点中元素个数

	int sum;  // 节点中元素和

	int rank;  // 搜索树的层级

	int flag;  // 0表示子节点都没访问过，1表示访问过左节点，2表示访问过左右节点

	vector <int> path;  // 节点元素

	Node();

	Node(const Node & nd);

};

// 默认构造函数

Node::Node()

{

	num = 0;

	sum = 0;

	rank = 0;

	flag = 0;

	// path is empty

}

// 复制构造函数

Node::Node(const Node & nd)

{

	num = nd.num;

	sum = nd.sum;

	rank = nd.rank;

	flag = nd.flag;

	path = nd.path;

}

// -----------------------------------------------------------------

void DFS(const vector <int> & deque)

{

	stack <Node *> stk;  // 存储节点对应的指针

	stack <Node *> pre_stk;  // 存储上一级节点（回溯队列）

	Node * now = new Node;  // 指向当前节点

	Node * next = NULL;  // 指向下一个节点

	Node * previous = NULL;  // 指向上一个节点

	while (now)

	{

		if (now->rank < deque.size() && (now->flag == 0))

		{

			// 左叶子节点,选择当前rank的数字

			next = new Node(*now);

			next->num++;

			next->sum += deque[next->rank];

			next->path.push_back(deque[next->rank]);

			next->rank++;

			next->flag = 0;

			stk.push(next);  // 将左节点加入堆栈中

			now->flag = 1;  // 改变标志位

			// 将当前节点作为上一级节点存储并删除

			previous = new Node(*now);

			pre_stk.push(previous);

			delete (now);

			// 取出堆栈中的待选节点作为当前节点

			now = stk.top();

			stk.pop();

			// 显示搜索路径

			for (int i = 0; i < next->path.size(); ++i)

			{

				cout << " " << next->path[i] << " ";

			}

			cout << endl;

			continue;  // DFS每次仅选取一个子节点，再进入下一步循环

		}

		if (now->rank < deque.size() && (now->flag == 1))

		{

			// 右节点，不选择当前rank的数字

			next = new Node(*now);

			next->rank++;

			next->flag = 0;

			stk.push(next);

			now->flag = 2;

			// 将当前节点作为上一级节点存储并删除

			previous = new Node(*now);

			pre_stk.push(previous);

			delete (now);

			// 取出堆栈中的待选节点作为当前节点

			now = stk.top();

			stk.pop();

			continue;

		}

		// 回溯结束

		if (pre_stk.empty())

		{

			break;

		}

		// 没有子节点或者没有未搜索过的子节点时，回退到上一级节点（回溯）

		if (now->rank >= deque.size() || now->flag == 2)

		{

			delete (now);

			now = pre_stk.top();

			pre_stk.pop();

		}

	}

}

// -----------------------------------------------------------------

int main()

{

	stack <Node*> stk;

	vector <int> deque { 2,3,5,7 };

	DFS(deque);

	cin.get();

	return 0;

}

运行结果

程序说明

1、定义了一个Node节点类，表示当前状态下已经搜索到的序列，path记录了这个子序列的值，并且类中添加了num（子序列中元素数目）、sum（子序列元素和）等属性，通过这些属性可以判断是否找到满意解或者用于剪枝。

2、对于原始序列中某个位置的数，其子序列中可以包含这个数，也可以不包含这个数，所以每次有两种选择，即每个节点有两个子节点。

3、flag属性标识了当前节点的子节点遍历情况。若flag=0，表示子节点都没访问过，下一步优先访问左节点，所以将左节点加入堆栈中；flag=1，表示访问过左节点，下一步访问右节点；flag=2，表示访问过左右节点。

4、当没有子节点（now->rank >= deque.size()）或者左右节点都访问过时（flag=2），回溯到上一级节点。

5、程序循环中，首先通过now当前节点，找到下一个子节点next，将其加入堆栈中，便于下一步循环。在now节点销毁前，将其存到previous，并加入pre_stk堆栈中。这样在下一轮循环中，previous相对于now就是上一级节点，如果now不能找到其子节点，就要返回上一级，这样previous就可以重新赋给now，达到返回上一级的目的。

6、整个程序的终止条件是pre_stk堆栈为空时截止，说明所有节点都已经遍历过，并且没有再可回溯的节点了。实际运用中，可以通过其他属性（搜索到可行解）来提前终止程序。

递归实现

参考自Coding_Or_Dead的博客

#include<cstdio>

#include <iostream>

int n, k; __int64 sum = 0;

int a[4] = { 2, 3, 5, 7 }, vis[4] = {0, 0, 0, 0};

void DFS(int i, int cnt, int sm)//i为数组元素下标,sm为cnt个数字的乘积

{

	if (cnt == k)  // 解中已包含k个数字

	{

		sum = sum + sm; return;

	}

	if (i >= n)

		return;

	if (!vis[i])

	{

		// 对第i个数字进行访问

		vis[i] = 1;

		//a[i]被选，优先选择第i个加入到解中，接下来搜索第i+1个数字

		DFS(i + 1, cnt + 1, sm*a[i]); 

		//a[i]不选，不选择第i个，相当于右节点，接下来搜素第i+1个数字

		DFS(i + 1, cnt, sm);

		vis[i] = 0;  // 回溯

	}

	return;

}

int main(void)

{

	n = 4, k = 2;

	DFS(0, 0, 1);

	printf("%I64d\n", sum);

	std::system("pause");

	return 0;

}

程序说明

1、程序目的：给定n个正整数，求出这n个正整数中所有任选k个相乘后的和，这里的数组a[4]存储原序列，vis[4]作为访问标志，k取2，结果输出为101，对应的序列是{2, 3}{2, 5}{2, 7}{3, 5}{3, 7}{5, 7}。

2、对于元素a[i]，每次对应两个选择。若选择将a[i]加入到解中，则解中元素个数+1，乘积结果*a[i]，所以下一步更新为DFS(i + 1, cnt + 1, sm*a[i])。若不选择a[i]，则解中的元素个数和乘积不变，下一步更新为DFS(i + 1, cnt, sm)。

3、回溯时要将标志位重置。

References