QK是一个很小的抢占式微内核调度程序，它专用用QP中。
QK的思想源于SST，Miro Samek重写了自己前期编的SST(Super Simple Task)代码。
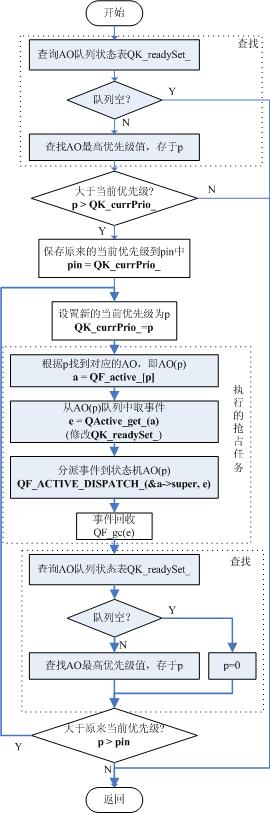
QK循环查询AO队列的状态表QK_readySet_,查找当前最高级的AO(活动对象，任务)，分发最高级AO队列中的事件到相对应的AO中。并在某事件消耗完时，回收事件。

QK的流程图如下：

QP之QK原理的更多相关文章

  1. QP之QEP原理

    1.QP简介: 量子平台(Quantum Platform, 简称QP)是一个用于实时嵌入式系统的软件框架,QP是轻量级的.开源的.基于层次式状态机的.事件驱动的平台. QP包括事件处理器(QEP). ...

  2. QP之QF原理

    1.QP简介: 量子平台(Quantum Platform, 简称QP)是一个用于实时嵌入式系统的软件框架,QP是轻量级的.开源的.基于层次式状态机的.事件驱动的平台. QP包括事件处理器(QEP). ...

  3. 基于raw os 的事件触发系统

    Raw os的事件触发系统有以下特点: 1 基于UML的状态机理念设计,实现了有限状态机(fsm)以及层次状态机(HSM). 2 实现了活动对象(ACTIVE OBJECT)的特性,一个活动对象包含了 ...

  4. SST-超级简单任务调度器结构分析

    SST(Super Simple Task) 是一个基于任务优先级.抢占式.事件驱动.RTC.单堆栈的超级简单任务调度器,它基于Rober Ward一篇论文的思想,Miro Samek用C重新编程实现 ...

  5. SpringBoot启动原理及相关流程

    一.springboot启动原理及相关流程概览 springboot是基于spring的新型的轻量级框架,最厉害的地方当属自动配置.那我们就可以根据启动流程和相关原理来看看,如何实现传奇的自动配置 二 ...

  6. IdentityServer4实现原理

    OAuth&OpenIDConnect是什么? 最近因为工作的原因,大概有两个月时间没写博客了,本来今年给自己的目标是每个月写一篇,或许记录工作中踩过的一些坑,或许学习一些新的技术框架.说实话 ...

  7. 【系统篇】从int 3探索Windows应用程序调试原理

    探索调试器下断点的原理 在Windows上做开发的程序猿们都知道,x86架构处理器有一条特殊的指令——int 3,也就是机器码0xCC,用于调试所用,当程序执行到int 3的时候会中断到调试器,如果程 ...

  8. java web学习总结(十四) -------------------JSP原理

    一.什么是JSP? JSP全称是Java Server Pages,它和servle技术一样,都是SUN公司定义的一种用于开发动态web资源的技术. JSP这门技术的最大的特点在于,写jsp就像在写h ...

  9. 深入解析SQL Server并行执行原理及实践(上)

    在成熟领先的企业级数据库系统中,并行查询可以说是一大利器,在某些场景下他可以显著的提升查询的相应时间,提升用户体验.如SQL Server, Oracle等, Mysql目前还未实现,而Postgre ...

随机推荐

  1. DEV控件之ChartControl用法 z

    一.总体概述 这个控件包含3层,最外面的chartControl层.中间的XYDiagram层.最里面的Series层.功能非常强大,但同时使用起来也相对复杂,需要各个层之间相互协调设置才能达到自己想 ...

  2. Eclipse启动JVM机制

    1.Eclipse启动的时候,会启动一个JVM来运行eclipse(因为Eclipse是Java代码实现的) 2.Eclipse启动一个带main的主类的时候,会单独启动一个JVM来运行他. 3.Ec ...

  3. RBTree和AVL

      红黑树和AVL的相同:都是平衡二叉树,所以插入删除修改查询都非常高效. 红黑树和AVL的区别: 红黑树:  不是要求绝对平衡,付出的代价是要着色,查询次数可能会多一层,好处是减少旋转次数. AVL ...

  4. ZT 或许你一辈子都是个小人物

    或许你一辈子都是个小人物 分类: 程序人生 2013-06-04 22:39 483人阅读 评论(2) 收藏 举报 程序人生 本文摘自:http://www.nowamagic.net/library ...

  5. Debian/Kali 安装原生Firefox

    出于种种原因,有很多人信仰原装纯净:就像debian下的iceweasel,有人总想换成firefox.好吧,正好最近29版发布了,我们无视掉这两者哥两好的关系,尝试在Debian/Kali 下安装F ...

  6. 误用MySQL关键字导致的错误

    使用Hibernate整合Spring的过程中,我使用explain作为表的字段,结果一直给我报错. 报错如下: ERROR: You have an error in your SQL syntax ...

  7. Map使用方法

    转:https://www.cnblogs.com/lzq198754/p/5780165.html Java map 详解 - 用法.遍历.排序.常用API等 概要: java.util 中的集合类 ...

  8. Selenium应用代码（常见封装的方法一）

    常见封装的方法:输入.点击.判断元素是否存在.根据句柄切换窗口.根据title切换窗口.滚动窗口.截图 import java.awt.Rectangle;import java.awt.image. ...

  9. mybatis会对多参数方法进行特殊处理

    例如:查询id=1,name=tom的一条数据 查询接口: User getUserByIdAndName(Integer id,String name); // <?xml version=& ...

  10. Unity中自定义扩展方法

    问题背景 在使用unity开发过程中,通常会遇到一种情况,比如说给物体重新赋值坐标的问题, Transfrom tran: ,pos_y=,pos_z=; tran.position=new Vect ...