Sumsets(3sum问题，枚举d,c二分a+b)

Sumsets

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 9997		Accepted: 2736

Description

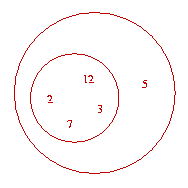Given S, a set of integers, find the largest d such that a + b + c = d where a, b, c, and d are distinct elements of S.

Input

Several S, each consisting of a line containing an integer 1 <= n <= 1000 indicating the number of elements in S, followed by the elements of S, one per line. Each element of S is a distinct integer between -536870912 and +536870911 inclusive. The last line of input contains 0.

Output

For each S, a single line containing d, or a single line containing "no solution".

Sample Input

5
2
3
5
7
12
5
2
16
64
256
1024
0

Sample Output

12
no solution
题解：给一个序列，让找不同的a,b,c,d在集合s中，使得a+b+c=d，如果能找到输出d，否则输出no solution；
乍一看完全没思路，也许不敢动手去写，可以选从大到小排序，枚举d,c；二分a+b等于d-c即可；

extern "C++"{
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
typedef long long LL;
void SI(int &x){scanf("%d",&x);}
void SI(double &x){scanf("%lf",&x);}
void SI(char *x){scanf("%s",x);}
//void SI(LL &x){scanf("%lld",&x);}

void PI(int &x){printf("%d",x);}
void PI(double &x){printf("%lf",x);}
void PI(char *x){printf("%s",x);}
//void PI(LL &x){printf("%lld",x);}

}
const int MAXN = 1010;
int a[MAXN];

int main(){
	int n;
	while(scanf("%d",&n),n){
		for(int i = 0;i < n;i++)SI(a[i]);
		sort(a,a + n);
		int ans,flot = 0;
		for(int i = n - 1;i >= 0;i--){
			if(flot)break;
			for(int j = n - 1;j >= 0;j--){
				if(flot)break;
				if(i == j)continue;
				int sum = a[i] - a[j],l = 0,r = j - 1;
				while(l < r){
					if(a[l] + a[r] == sum && i != l && i != r){
						ans = a[i];
						flot = 1;
						break;
					}
					if(a[l] + a[r] > sum)
						r--;
					else
						l++;
				}
			}
		}
		if(flot)
			printf("%d\n",ans);
		else
			puts("no solution");
	}
	return 0;
}