IoC（控制反转）和DI(依赖注入)

一、IOC

1.目标类

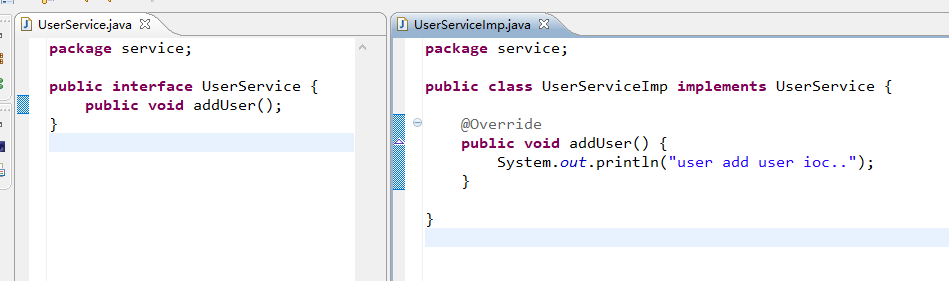
• 提供UserService接口和实现类
• 获得UserService实现类的实例

　　之前开发中，直接new一个对象即可，使用spring之后，将由spring创建  --》IoC控制反转

以后需要实例对象时，从spring工厂（容器）获得，需要将实现类的全限定名称配置到xml中

2.配置文件

位置：任意，开发一般放在classpath下（src）

名称：任意，一般使用applicationContext.xml

内容：添加schema约束

约束文件位置：spring-framework-3.2.0.RELEASE\docs\spring-framework-reference\html\xsd-config.html

<?xml version="1.0" encoding="UTF-8"?>
<beans xmlns="http://www.springframework.org/schema/beans"
       xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
       xsi:schemaLocation="http://www.springframework.org/schema/beans
                              http://www.springframework.org/schema/beans/spring-beans.xsd">

    <!-- bean definitions here
    配置所需要创建的实例对象，放入spring容器中
    -->
    <bean class="service.UserServiceImp" id="userService"></bean>
</beans>

3.测试

@Test
public void test01(){
    //获得容器
    String xmlPath = "service/beans.xml";
    ApplicationContext applicationContext = new ClassPathXmlApplicationContext(xmlPath);
    //从容器中取实例对象
    UserService userService = (UserService) applicationContext.getBean("userService");
    System.out.println(userService);
    userService.addUser();
}

二、DI

1.目标类

2.配置文件

<bean id="userService" class="DI.UserServiceImp">
    <!-- 属性注入，
        name:属性名，通过set方法获得
        ref:另一个bean的id的引用
     -->
    <property name="userDao" ref="userDao"></property>
</bean>
<bean id="userDao" class="DI.UserDaoImp"></bean>

3.测试

@Test
public void test01(){
    //获得容器
    String xmlPath = "DI/beans.xml";
    ApplicationContext applicationContext = new ClassPathXmlApplicationContext(xmlPath);
    //从容器中取实例对象
    UserService userService = (UserService) applicationContext.getBean("userService");
    System.out.println(userService);
    userService.addUser();
}