开放定址法——平方探测(Quadratic Probing)

为了消除一次聚集，我们使用一种新的方法：平方探测法。顾名思义就是冲突函数F(i)是二次函数的探测方法。通常会选择f(i)=i²。和上次一样，把{89,18,49,58,69}插入到一个散列表中，这次用平方探测看看效果，再复习一下探测规则：h_i(x)= ( Hash(x) + F(I) ) % TableSize（I=0,1,2…）

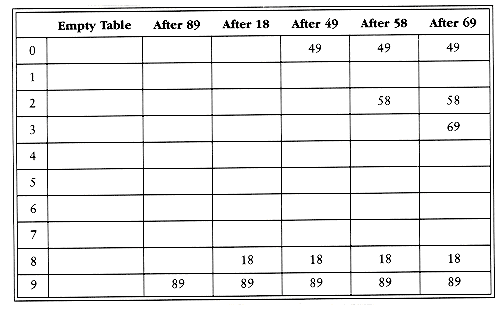
脑内调试一下：49和89冲突时，下一个空闲位置是0号单元。58和18冲突时，i=1也冲突，再试i=2，h₂(58)=(8+4)%10=2是空的可以放。69同理。

对于线性探测法而言，我们得避免元素几乎填满的情况，因为这时候性能会急剧降低。对于平方探测法，这会更糟：如果表超过一半被填满，那当表的规模不是素数时，甚至在表被填满一般之前就已经不能一下找到空单元了，需要试探好几次才能找到一个空单元。原因是表最多有一半位置可以用来解决冲突。凭什么如此断言呢？Talk is cheap,show me your….proof.

定理

如果使用平方探测，且表的规模是素数，那么当表至少有一半是空的时候，总能插入新的元素。

我们假设表的Size是一个大于3的素数，直接拿着定理证明有点让人不知所措，那把这个定理的证明转化为：证明“前$\frac{\mbox{Si}ze}{2}$个备选位置是互异的”，然后用反证法。从所有前$\frac{\mbox{Si}ze}{2}$个的位置里选两个：（ h(x) + i² ）%Size和（ h(x) + j² ）%Size,其中 0 < i，j$ \leq  \frac{\mbox{Si}ze}{2}$。假设这两个位置相同，且i ≠ j，然后让他们位置相等，推出矛盾就行了，因为都mod Size，根据等式性质我们只需要考察括号里的项就行了。

　　（h(x) + i²）=（h(x) + j²）

　=>   i² = j²

　=>  (i-j)(i+j) = 0

前面说了i ≠ j,所以只可能i = - j。但是这和他们的定义域矛盾，所以也是不可能的。所以前一半位置互异，可供选择，任何元素都有$\frac{\mbox{Si}ze}{2}$个可能被放的位置。综上，如果最多有一半的位置可用，那么空闲单元总是能找到的。反过来讲，哪怕表里有一半+1个位置被填上，那么插入都有可能失败（虽然这比较偶然，但还是有可能的），这一点是十分重要的，要拿小本本记下来，说不定校招或考研就出题了哈哈哈。另外保证Size是素数也是非常重要的，如果不是的话，那遭遇冲突时可供选择的空单元个数会锐减到你难以置信的地步，远比一半少，这样一来，我们的战略纵深就太小了，难以迂回，这种情况没人希望见到。

Size=16的时候，找备选的单元只能取i=1,2,3，也就是距离冲突单元1,4,9个单位的位置了。

另外，在开放定址的散列表里，我们之前意义上的删除操作是不能进行的，因为某个数对应的单元可能已经引起过冲突了，然后他探测跑到别的位置了。比如我们要删除69，你find一下，定位到9，发现那躺着89，那我们只能跟着平方探测的思路再找找9+1²，结果发现还不对，在那的是58。得，继续找吧，试试9+2^2，这才找到。想想吧，这才Size=10就这么费劲了，那企业级软件要处理千万级甚至亿级的数据怎么办，比如头条app的数据量，那程序还不跑到天荒地老。。。因此开放定址散列表需要懒惰删除。

谈谈怎么实现吧，先给出类型声明。在这里我们不用结构体数组，而使用散列表单元的数组，而且单元是动态分配地址这和分离链接一样。

#ifndef HashQuad_h
#define HashQuad_h
typedef unsigned int Index;
typedef Index Position;
struct HashTb1;
typedef struct HashTb1 *HashTable;

HashTable Init(int size);
void DestroyTable(HashTable H);
void Insert(int key, HashTable H);
Position Find(int key,HashTable H);
int Retrieve(Position P);
HashTable ReTable(HashTable H);
#endif /* HashQuad_h */

enum KindOfEntry{
    Legitimate,
    Empty,
    Deleted
};

struct HashEntry {
    int value;
    enum KindOfEntry Info;
};

typedef struct HashEntry Cell;

/*Cell *TheCells will be an array of 
 HashEntry cells,allocated later
 */
struct HashTb1 {
    int TableSize;
    Cell *TheCells;
};

顺便一说，Hash函数还是设置为简单的%Size

Index Hash(int key,int size) {
    return key%size;
}

初始化由2步组成：分配空间，然后将每个单元的Info设置为Empty。

#define aPrime 307
#define MinTableSize 5

HashTable Initial(int size){
    HashTable H;
    int i;
    if (size<MinTableSize) {
        printf("Table size too small\n");
        return NULL;
    }
    
    //Allocate table
    H=(HashTable)malloc(sizeof(struct HashTb1));
    H->TableSize=aPrime;
    
    //Allocate array of cells
    H->TheCells=(Cell*)malloc(sizeof(Cell)*H->TableSize);
    
    //Allocate list headers
    for (i=; i<H->TableSize; i++)
        H->TheCells[i].Info=Empty;
    return H;
}

和分离链接一样，Find返回key在散列表里的单元号码。而且因为被标记了Empty，我们想表达查找失败也很容易。

 Position Find(int key,HashTable H){
     Position cur;
     int CollisionNum=;
     cur=Hash(key,H->TableSize);
     while (H->TheCells[cur].Info != Empty &&
            H->TheCells[cur].value!= key)
     {
         cur+= (++CollisionNum<<) - ;
         if (cur>=H->TableSize)
             cur-=H->TableSize;
     }
     return cur;
 }

第8行到第10行是进行平方探测的快速方法，因为在实现的时候不太好判断进行到第几次探测了，所以直接算i^2不容易，另设个变量监测倒也可以，不过那样挺麻烦的，还占用空间，还多了一次监测变量的++，还多了一次判断，还多了一次平方运算，尤其是算平方开销太大了。所有的这些都会让效率变低。所以我们要把平方计算转化为单纯的+-计算，用i² - ( i - 1 )²算出他们之间的差距是2 * i - 1，所以F(i)=F( i - 1 ) + 2 * i - 1这个几乎全是加减，乘法用移位代替速度就快多了。如果新的定位越过数组，那么可以通过-Size把它拉回到数组的范围里。这比通常办法快多了，因为他避免了看似要做的乘法和平方。第行的判断顺序很重要，别翻过来，不然短路性质就用不上了。

然后说插入，如果Key存在，就什么也不做，否则就把插入元素放在Find的位置。

void Insert(int key, HashTable H){
    Position P=Find(key, H);
    if (H->TheCells[P].Info != Legitimate)
    {
        H->TheCells[P].Info=Legitimate;
        H->TheCells[P].value=key;
    }
}

虽然平方探测法排除了一次聚集，但是散列到同一位置上的元素将探测相同的备选单元，这么说有点抽象，就是探测的时候都会踩同样的坑，比如说89，49，69这三个数往散列表里放，h₀(49)撞到89了，试试i=1，可以了。69撞到89了然后试试i=1,算完之后h₁(69)=0和h₁(49)又撞了，这就叫“探测到相同的备选单元”，再试一次69才被安置。想想规模更大的表，相撞次数会更多，用f(i)=i²探测的时候分批扎堆，这就叫二次聚集，和之前相比，不是0，1，2，3这样连着一整块扎堆，而是在i=1，4，9，16附近扎堆。这是这两种聚集的区别。

二次聚集是理论上的一个缺憾，下一篇里我们继续讨论如何排除这个缺憾，从而对散列表冲突问题的排解更为高效和优美。不过这需要花费另外一些时间去做乘除法，比平方探测单纯的加减法慢一些，有利有弊吧，实际场景里因地制宜地选择不同模型就好。