P3943 星空 区间异或差分

\(\color{#0066ff}{ 题目描述 }\)

逃不掉的那一天还是来了，小 F 看着夜空发呆。

天上空荡荡的，没有一颗星星——大概是因为天上吹不散的乌云吧。

心里吹不散的乌云，就让它在那里吧，反正也没有机会去改变什么了。

小 C 拿来了一长串星型小灯泡，假装是星星，递给小 F，想让小 F 开心一点。不过，有 着强迫症的小 F 发现，这串一共 n 个灯泡的灯泡串上有 k 个灯泡没有被点亮。小 F 决定 和小 C 一起把这个灯泡串全部点亮。

不过，也许是因为过于笨拙，小 F 只能将其中连续一段的灯泡状态给翻转——点亮暗灯 泡，熄灭亮灯泡。经过摸索，小 F 发现他一共能够翻转 m 种长度的灯泡段中灯泡的状态。

小 C 和小 F 最终花了很长很长很长很长很长很长的时间把所有灯泡给全部点亮了。他 们想知道他们是不是蠢了，因此他们找到了你，让你帮忙算算：在最优的情况下，至少需要 几次操作才能把整个灯泡串给点亮？

\(\color{#0066ff}{输入格式}\)、

从标准输入中读入数据。

输入第 1 行三个正整数 n,k,m。

输入第 2 行 \(k\) 个正整数，第 i 个数表示第 i 个被没点亮的灯泡的位置 \(a_i\)

输入第 3 行 \(m\) 个正整数，第 i 个数表示第 i 种操作的长度 \(b_i\)

保证所有 \(b_i\) 互不相同；保证对于 \(1 \le i < k\)，有 \(a_i< a_i+1\)；保证输入数据有解。

\(\color{#0066ff}{输出格式}\)

输出标准输入中。

输出一行一个非负整数，表示最少操作次数。

\(\color{#0066ff}{输入样例}\)

5 2 2
1 5
3 4

\(\color{#0066ff}{输出样例}\)

2

\(\color{#0066ff}{数据范围与提示}\)

【样例 1 解释】

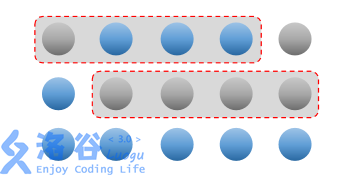
【数据范围与约定】

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解 决一部分测试数据。

每个测试点的数据规模及特点如下表

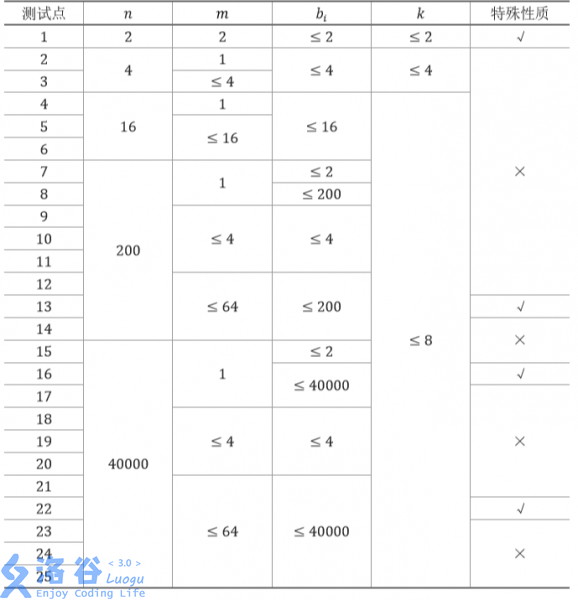
特殊性质：保证答案小于 4

\(\color{#0066ff}{ 题解 }\)

每次区间异或，而且区间长度比较长，于是考虑差分，转为两个端点的异或

总共要翻转k个灯， 因此差分序列长度最多为2k且一定是偶数个

每次可以消除两个1，消除的代价与距离有关，现在问题转为把所有1消去的最小代价

消除的代价可以用完全背包来求，设\(v[i]\)为翻转长度为i的区间的最小代价

把每个翻转操作的长度当做两个物品x和-x，一个是影响作用\(0\to1\)，一个是抵消作用\(1\to0\)

这样代价可以\(O(nm)\)的求出来

然后可以愉快的DP了，显然要状压2k的1

直接设\(f[i]\)为i到达i状态的最小代价，转移的时候，枚举两个1转移即可

总复杂度\(O(nm+4^kk^2)\)

#include<bits/stdc++.h>
#define LL long long
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
const int maxn = 1e5 + 10;
int n, k, m, num;
int t[maxn], v[maxn], b[maxn], f[1002020];
void dfs(int zt) {
	for(int i = 1; i <= num; i++) {
		if(!(zt & (1 << (i - 1)))) continue;
		for(int j = i + 1; j <= num; j++) {
			if(!(zt & (1 << (j - 1)))) continue;
			int now = zt ^ (1 << (i - 1)) ^ (1 << (j - 1));
			if(f[now] > f[zt] + v[t[j] - t[i]]) {
				f[now] = f[zt] + v[t[j] - t[i]];
				dfs(now);
			}
		}
	}
}

int main() {
//	freopen("starlit.in", "r", stdin);
//	freopen("starlit.out", "w", stdout);
	n = in(), k = in(), m = in();
	int x;
	for(int i = 1, ls = -1; i <= k; i++) {
		x = in();
		if(x == ls + 1) t[num] = x + 1;
		else t[++num] = x, t[++num] = x + 1;
		ls = x;
	}
	memset(v, 0x3f, sizeof v);
	v[0] = 0;
	for(int i = 1; i <= m; i++) b[i] = in();
	for(int i = 1; i <= m; i++)
		for(int j = b[i]; j <= n; j++)
			v[j] = std::min(v[j], v[j - b[i]] + 1);
	for(int i = 1; i <= m; i++)
		for(int j = n - b[i]; j >= 0; j--)
			v[j] = std::min(v[j], v[j + b[i]] + 1);
	memset(f, 0x3f, sizeof f);
	f[(1 << num) - 1] = 0;
	dfs((1 << num) - 1);
	printf("%d", f[0]);
	return 0;
}