【Support Vector Regression】林轩田机器学习技法

上节课讲了Kernel的技巧如何应用到Logistic Regression中。核心是L2 regularized的error形式的linear model是可以应用Kernel技巧的。

这一节，继续沿用representer theorem，延伸到一般的regression问题。

首先想到的就是ridge regression，它的cost函数本身就是符合representer theorem的形式。

由于optimal solution一定可以表示成输入数据的线性组合，再配合Kernel Trick，可以获得ridge regression的kernel trick形式。

这样就获得了kernel ridge regression的analytic solution形式。

但是这样算出来的beita是非常dense的。

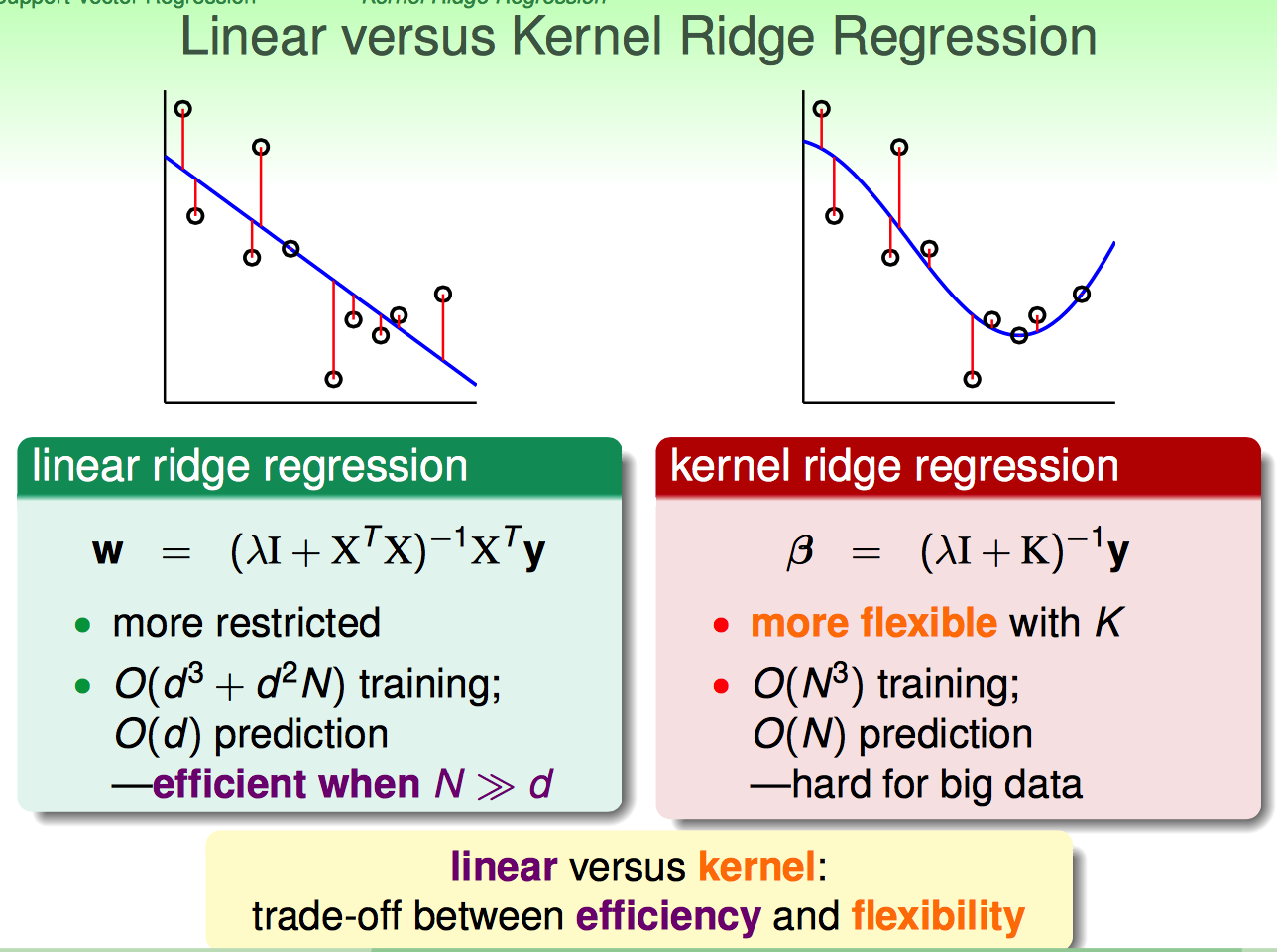
因此，对比linear和kernel ridge regression：

（1）linear的效率可能要比kernel的高，尤其是N很大的时候

（2）kernel的灵活性要好（弯弯曲曲的），但是一旦N很大基本就废了

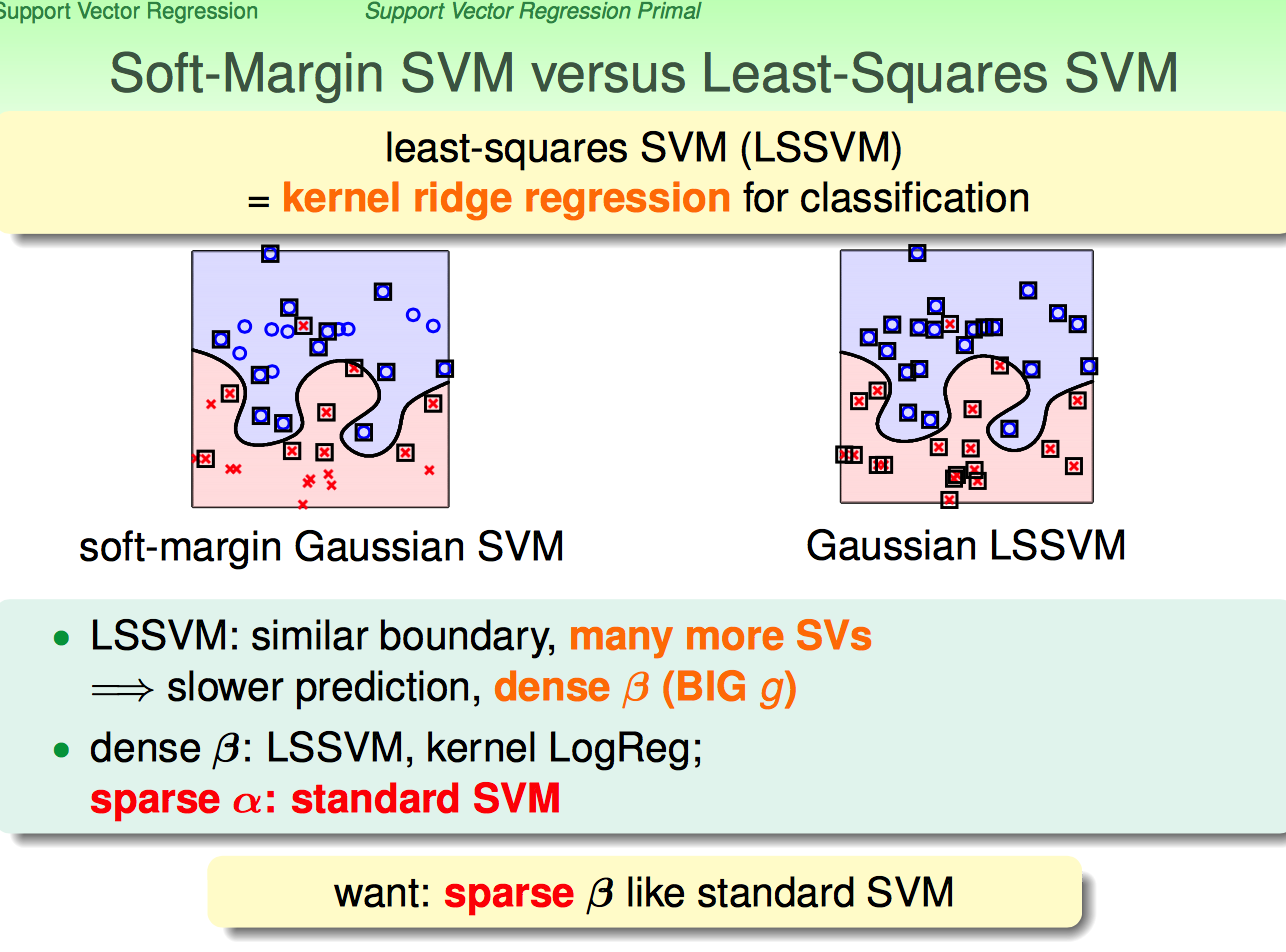
上面个说的这种kernel ridge regression for classification有个正式的名称叫“least-squares SVM (LSSVM)”

对比原来的Soft-Margin SVM，LSSVM的support vectors多了很多；再由于W是Support Vectors的线性组合，这就意味这在predict的时候要耗费更多的时间。

现在问题来了，能否用什么方法，把这种一般的regression for classification问题转换成SVM那种sparse support vectors的形式呢？

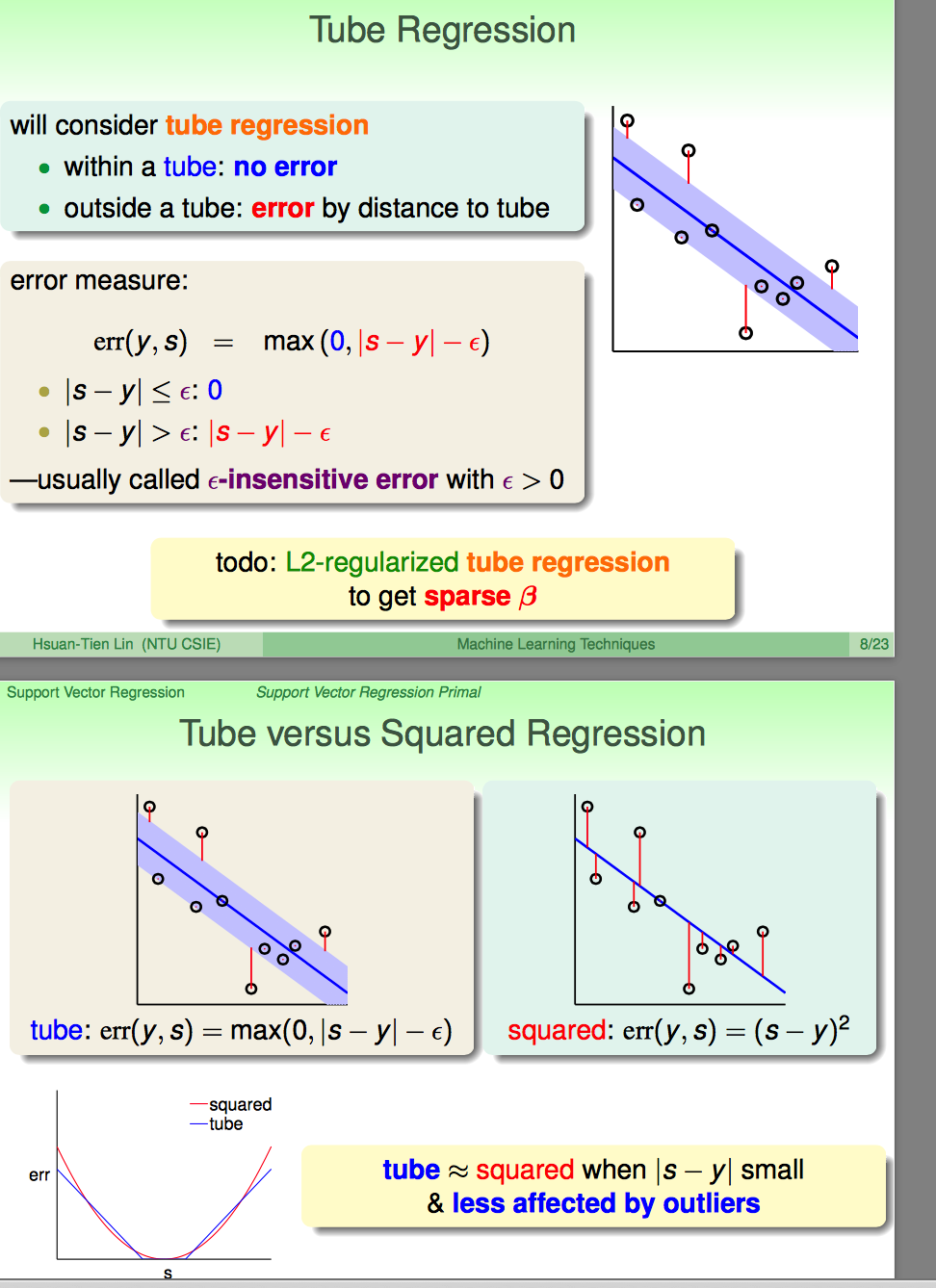
这里引入了一种新的regression叫tube regression的方式：

（1）tube的核心在于error measure的方式：epsilon insensitive error的方式

（2）引入L2 regularized tube regression来实现sparse support vectors

（3）对比这种epsilon insensitive error和square error，可以看score与y相差较远时，tube似乎受到outliers的影响更小一些

更进一步，把L2-Regularized用到Tube Regression上面就形成了如下的cost function。

L2-Regularized Tube Regression的cost function虽然是无约束的，但是是不可导的，并且也看不出来啥sparsity的可能。

那么，能否模仿standard SVM的技巧，换成有约束但是可导的cost function呢？

（1）如果直接模仿SVM的cost function形式：引入一个kesin；貌似长得很像SVM了，但是由于带了个绝对值，所以还是不能求导

（2）这时候，前人的智慧就派上用场了：

　　　　a. 引入kesin up代表score比yn大出epsilon的容忍范围

　　　　b. 再引入kesin down代表score比yn小出epsilon的容忍范围

　　　　c. 修改cost function的形式：把kesin up和kesin down都放到里面

总的来说，就是引多引入了N个变量，多了N个constraints；结果最终把L2-regularized Tube Regression的cost function转化成了Quadratic Programming的问题。

紧接着，能否再转化为dual问题求解呢？（引入kernel容易一些？）

引入两套Lagrange Multipliers。

再配合上KKT条件，就可以得到dual形式的Quadratic Programming的问题形式。

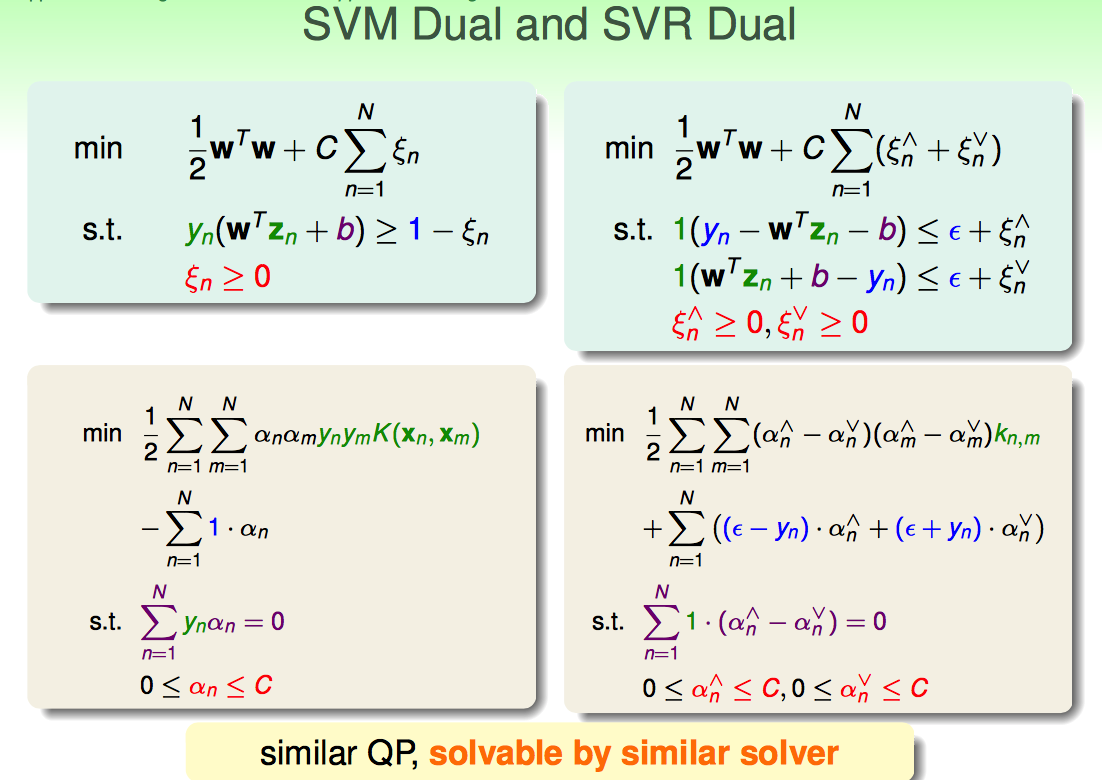
最终dual形式与soft-margin形式的svm非常类似。

根据representer theorem，只有outside tube或者on tube上的点才是支撑向量。虽说这种sparsity感觉怪怪的，但毕竟已经比原来的LLSVM好很多了。